
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цели анализа последовательных алгоритмов
Основы построения графа алгоритма 3. Допустимые преобразования алгоритма Цели анализа последовательных алгоритмов Появление параллельных вычислительных систем и внедрение их в практику решения больших прикладных задач привело к возникновению целого ряда проблем в области численного программного обеспечения. Построение новых численных методов для параллельных вычислительных систем процесс долговременный и сложный. Попытки разработать специальные параллельные методы не всегда оказывались состоятельными [1]. Кроме того, непростительно просто отбросить при работе на параллельных ЭВМ огромный багаж численных методов и программ, накопленный в процессе длительного использования последовательных компьютеров. Актуальны не только исследования “классических” последовательных алгоритмов для определения возможности их использования в параллельных вычислительных системах, но и сведения о параллельных свойствах алгоритмов, а также знания, позволяющие эти сведения получать. Эффективное использование различного типа параллельных вычислительных систем возможно за счет одновременного выполнения ими ветвей вычислений, не связанных между собой информационно. Поэтому целью исследования последовательного алгоритма является поиск и выделение таких ветвей. Если они найдены, говорят, что алгоритму присущ внутренний параллелизм, и его принципиально возможно реализовать на параллельной вычислительной системе, в противном случае его использование в ней нецелесообразно. Одной из возможных форм записи алгоритмов является их представление в виде графов (грубо говоря, любая блок-схема алгоритма также может с определенными оговорками рассматриваться как граф) [2].
Основы построения графа алгоритма При построении графа алгоритма никаких существенных ограничений на вид переменных и операций не накладывается. Переменными могут быть числа, буквы алфавита, логические переменные, матрицы, массивы и т.д., операциями – любые арифметические, логические, матричные операции и т.п. Предполагается, что число входов и выходов (аргументов и результатов) каждой операции алгоритма в терминах выбранных переменных фиксировано и не зависит от общего числа всех операций алгоритма.
Множеству операций алгоритма, реально выполняемых при заданных входных данных, ставится во взаимно однозначное соответствие множество вершин графа. Если аргумент одной операции есть результат выполнения другой операции, то соответствующие вершины образуют ребро, направленное из той вершины, откуда берется результат. Вершины графа, отвечающие операциям ввода (входным данным), не будут иметь входящих дуг, а операциям вывода – выходящих. При этом совсем не обязательно, чтобы одному и тому же входному данному соответствовала одна входная вершина (одна операция ввода). Число подобных операций может выбираться, исходя из конкретных условий. Аналогично с операциями вывода. В тех случаях, когда изображение графа является достаточно громоздким, возможно не изображать входные и выходные вершины, считая их положение ясным по умолчанию. Описанный граф – граф информационной зависимости реализации алгоритма при фиксированных входных данных [Воев], который для удобства далее называется графом алгоритма. Граф алгоритма Пример 10. Необходимо вычислить значение выражения
Порядок выполнения операций в правой части выражения однозначно не определен: например, произведение
Таблица 8.1- Последовательность операций
Очевидно, что графы, отвечающие различным последовательностям операций для рассматриваемого примера (рис.8.1), являются изоморфными.
Рис.8.1
По существу, в (100) фиксирован не один алгоритм, а несколько математически эквивалентных. Пример 20. Исследовать различные способы вычисления суммы
В точной арифметике операция сложения обладает свойством коммутативности и ассоциативности. Очевидно, что общее число различных способов вычисления выражения (150) при больших
которой соответствует граф
соответствующий граф которой:
Можно показать, что схема последовательного суммирования хуже по точности, чем схема сдваивания, примерно, в Замечание. Графы алгоритмов примера 10 и схемы сдваивания примера 20 очевидно являются изоморфными, хотя соответствуют решению совершенно разных задач. Алгоритмы с изоморфными графами обладают многими общими свойствами, по крайней мере, в той части, которая касается распределения информации при реализации алгоритмов (хотя призваны решать возможно совершенно разные задачи). Замечание. Графы алгоритмов примеров 10, 20 имеют достаточно ясную и простую структуру, которая определяется не только самими алгоритмами. Во многом она зависит и от того, как конкретно на плоскости выбраны места расположения вершин. При случайном выборе расположения вершин структуру графа можно не разглядеть. Задачу выбора наилучшего расположения вершин можно пытаться решить, если число вершин невелико. При этом, возможно, придется использовать полный перебор рассматриваемых вариантов. В типичных ситуациях число операций алгоритма огромно, более того, чаще всего оно даже точно не определено и задается какими-нибудь параметрами. В этих случаях использование полного перебора вариантов для решения задачи о построении и исследовании графа алгоритма практически нереально.
3. Допустимые преобразования алгоритма Граф алгоритма не накладывает на порядок выполнения операций никаких ограничений, кроме одного: к моменту начала реализации любой операции должны закончить свое выполнение все те операции, которые поставляют для нее аргументы. Таким образом, граф алгоритма определяет некоторое множество допустимых порядков выполнения операций, показывая, как при этом происходит распространение информации. Утверждение 100. Пусть при выполнении операций ошибки округлений определяются только значениями аргументов операций. Тогда при одних и тех же входных данных все реализации алгоритма, соответствующие одному и тому же графу, дают один и тот же результат, включая всю совокупность ошибок округления, независимо от порядка выполнения операций [Воев].
Доказательство. Разобьем множество вершин графа алгоритма Замечание 100. При реализации алгоритма либо алгоритм в целом, либо отдельные его фрагменты иногда приходится подстраивать под особенности вычислительной техники. Эта подстройка фактически означает преобразование алгоритма. Из утверждения 100 вытекает, что преобразования сохраняют уровень достоверности результатов и, следовательно, являются допустимыми, если эти преобразования сохраняют граф алгоритма.
Вопросы 1. Почему исследования “классических” последовательных алгоритмов для определения возможности их использования в параллельных вычислительных системах остаются актуальными в настоящее время? 2. Что такое внутренний параллелизм алгоритма? Любому ли алгоритму присущ внутренний параллелизм? 3. Что представляет из себя граф информационной зависимости реализации алгоритма? 4. Какие ограничения накладывает граф алгоритма на порядок выполнения операций? 5. Какие преобразования алгоритма сохраняют уровень достоверности его результатов?
Литература 1. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с. 2. Харари Ф. Теория графов / Ф.Харари; пер.с англ. В.П.Козырева. — М.: Мир, 1973. — 300 с. 3. Уилсон Р. Введение в теорию графов / Р.Уилсон. — М.: Мир, 1977. — 207 с. 4. Кристофидес Н. Теория графов. Алгоритмический подход / Н.Кристофидес. — М.: Мир, 1978. — 432 с. 5. Новиков Ф.А. Дискретная математика для программистов / Ф.А.Новиков. — СПб.: Питер, 2006. — 364 с. 6. Иванов Б.Н. Дискретная математика. Алгоритмы и программы / Б.Н.Иванов. — М.: Лаборатория Базовых Знаний, 2001. — 288с.
Лекция 9. Топологическая сортировка графа План
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 742; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.137.218 (0.019 с.) |
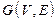 , где V — множество вершин графа, а E — множество его ребер, является ориентированным ациклическим мультиграфом (в мультиграфе не допускаются петли, но допускаются кратные ребра).
, где V — множество вершин графа, а E — множество его ребер, является ориентированным ациклическим мультиграфом (в мультиграфе не допускаются петли, но допускаются кратные ребра). . (100)
. (100) можно вычислить на первом шаге, а можно после нахождения значения
можно вычислить на первом шаге, а можно после нахождения значения  . Существует и множество других вариантов, некоторые из которых представлены в следующей таблице 8.1. Операции на одном шаге могут выполняться одновременно (параллельно), сами шаги выполняются последовательно.
. Существует и множество других вариантов, некоторые из которых представлены в следующей таблице 8.1. Операции на одном шаге могут выполняться одновременно (параллельно), сами шаги выполняются последовательно.


 . (150)
. (150)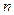 будет очень значительным. Какой способ выбрать? С точки зрения точных вычислений все они эквивалентны. Но в условиях влияния ошибок округления появляются значительные различия. Рассмотрим две возможных реализации вычисления (150) при
будет очень значительным. Какой способ выбрать? С точки зрения точных вычислений все они эквивалентны. Но в условиях влияния ошибок округления появляются значительные различия. Рассмотрим две возможных реализации вычисления (150) при  :
: ,
,
 ,
,
 раз. Различия есть и в информационных связях между отдельными операциями. Хотя оба графа имеют одно и тоже число вершин и соответствуют одному и тому же вычисляемому выражению (150), эти графы не изоморфны (у них разные длины критических путей), перенос информации в соответствующих им схемах осуществляется принципиально различными способами. Как видно из первого графа, схема последовательного суммирования не имеет никаких параллельных ветвей вычислений. второй граф показывает наличие в схеме сдваивания большого числа информационно не связанных между собой, а значит имеющих возможность выполняться одновременно, операций.
раз. Различия есть и в информационных связях между отдельными операциями. Хотя оба графа имеют одно и тоже число вершин и соответствуют одному и тому же вычисляемому выражению (150), эти графы не изоморфны (у них разные длины критических путей), перенос информации в соответствующих им схемах осуществляется принципиально различными способами. Как видно из первого графа, схема последовательного суммирования не имеет никаких параллельных ветвей вычислений. второй граф показывает наличие в схеме сдваивания большого числа информационно не связанных между собой, а значит имеющих возможность выполняться одновременно, операций. на подмножества
на подмножества  , где
, где  содержит только входные вершины, а в вершины из множества
содержит только входные вершины, а в вершины из множества  входят дуги лишь из вершин, принадлежащих множествам
входят дуги лишь из вершин, принадлежащих множествам  . Независимо от порядка выполнения операций, каждая из вершин
. Независимо от порядка выполнения операций, каждая из вершин  даст один и тот же результат. Действительно, аргументами операций являются входные данные, эти данные не зависят от порядка выполнения операций. Результаты выполнения операций в
даст один и тот же результат. Действительно, аргументами операций являются входные данные, эти данные не зависят от порядка выполнения операций. Результаты выполнения операций в  , тогда результаты выполнения операций в
, тогда результаты выполнения операций в 


