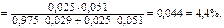Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Независимые случайные события. Теорема умножения вероятностей
Случайные события называются независимыми, если появление одного из них никак не влияет на вероятность появления других событий. Пример 1. Если есть две или более урны с цветными шарами, то извлечение какого-либо шара из одной урны никак не повлияет на вероятность извлечения других шаров из оставшихся урн. Для независимых событий справедлива теорема умножения вероятностей: вероятность совместного (одновременного) появления нескольких независимых случайных событий равна произведению их вероятностей: Р(А1и А2 и А3 … и Аk) = Р(А1) ∙Р(А2) ∙…∙Р(Аk). (7) Совместное (одновременное) появление событий означает, что происходят события и А1, и А2 , и А3 … и Аk. Пример 2. Есть две урны. В одной находится 2 черных и 8 белых шаров, в другой – 6 черных и 4 белых. Пусть событие А –выбор наугад белого шара из первой урны, В – из второй. Какова вероятность выбрать наугад одновременноиз этих урн по белому шару, т.е. чему равна Р (А и В)? Решение: вероятность достать белый шар из первой урны Пример 3. Рацион с пониженным содержанием йода вызывает увеличение щитовидной железы у 60% животных большой популяции. Для эксперимента нужны 4 увеличенных железы. Найдите вероятность того, что у 4 случайно выбранных животных будет увеличенная щитовидная железа. Решение:Случайное событие А – выбор наугад животного с увеличенной щитовидной железой. По условию задачи вероятность этого события Р (А) = 0,6 = 60%. Тогда вероятность совместного появления четырех независимых событий – выбор наугад 4 животных с увеличенной щитовидной железой – будет равна: Р (А 1 и А 2 и А 3 и А 4) = 0,6 ∙ 0,6 ∙0,6 ∙ 0,6=(0,6)4 ≈ 0,13 = 13%. Зависимые события. Теорема умножения вероятностей для зависимых событий Случайные события А и В называются зависимыми, если появление одного из них, например, А изменяет вероятность появления другого события – В. Поэтому для зависимых событий используются два значения вероятности: безусловнаяи условнаявероятности. Если А и В зависимыесобытия, то вероятность наступления события В первым (т.е. до события А) называется безусловной вероятностью этого события и обозначается Р (В).Вероятность наступления события В при условии, что событие А уже произошло, называется условной вероятностью события В и обозначается Р (В / А) или РА (В).
Аналогичный смысл имеют безусловная – Р (А) и условная – Р (А/В) вероятности для события А. Теорема умножения вероятностейдля двух зависимых событий: вероятность одновременного наступления двух зависимых событий А и В равна произведению безусловной вероятности первого события на условную вероятность второго: Р (А и В) = Р (А) ∙Р (В/А), (8) если первым наступает событие А, или Р (А и В) = Р (В) ∙Р (А/В), (9) если первым наступает событие В. Пример 1.В урне 3 черных шара и 7 белых. Найдите вероятность того, что из этой урныодин за другим(причем первый шар не возвращают в урну) будут вынуты 2 белых шара. Решение: вероятность достать первый белый шар (событие А) равна 7/10. После того как он вынут, в урне остается 9 шаров, из них 6 белых. Тогда вероятность появления второго белого шара (событие В) равна Р (В / А) = 6/9, а вероятность достать подряд два белых шара равна Р (А и В) = Р (А)∙ Р (В / А) = Приведенная теорема умножения вероятностей для зависимых событий допускает обобщение на любое количество событий. В частности, для трех событий, связанных друг с другом: Р (А и В и С) = Р (А) ∙ Р (В/А) ∙ Р (С/АВ). (10) Пример 2. В двух детских садах, каждый из которых посещает по 100 детей, произошла вспышка инфекционного заболевания. Доли заболевших составляют соответственно 1/5 и 1/4, причем в первом учреждении 70 %, а во втором – 60 % заболевших – дети младше 3-х лет. Случайным образом выбирают одного ребенка. Определите вероятность того, что: 1) выбранный ребенок относится к первому детскому саду (событие А) и болен (событие В). 2) выбран ребенок из второго детского сада (событие С), болен (событие D) и старше 3-х лет (событие Е). Решение. 1) искомая вероятность – Р (А и В) = Р (А) ∙ Р (В / А) = 2) искомая вероятность: Р (С и D и Е) = Р (С) ∙ Р (D / C) ∙ Р (Е / CD) = Формула Байеса
Пример1. При первичном осмотре больного предполагаются 3 диагноза Н 1, Н 2, Н 3. Их вероятности, по мнению врача, распределяются так: Р (Н 1) = 0,5; Р (Н 2) = 0,17; Р (Н 3) = 0,33. Следовательно, предварительно наиболее вероятным кажется первый диагноз. Для его уточнения назначается, например, анализ крови, в котором ожидается увеличение СОЭ (событие А). Заранее известно (на основании результатов исследований), что вероятности увеличения СОЭ при предполагаемых заболеваниях равны:
Р (А / Н 1) = 0,1; Р (А / Н 2) = 0,2; Р (А / Н 3) = 0,9. В полученном анализе зафиксировано увеличение СОЭ (событие А произошло). Тогда расчет по формуле Байеса (12) дает значения вероятностей предполагаемых заболеваний при увеличенном значении СОЭ: Р (Н 1/ А) = 0,13; Р (Н 2/ А) = 0,09; Пример 2. Определите вероятность, оценивающую степень риска перинатальной* смертности ребенка у женщин с анатомически узким тазом. Решение: пусть событие Н 1 – благополучные роды. По данным клинических отчетов, Р (Н 1) = 0,975 = 97,5 %, тогда, если Н2 – факт перинатальной смертности, то Р (Н 2) = 1 – 0,975 = 0,025 = 2,5 %. Обозначим А – факт наличия узкого таза у роженицы. Из проведенных исследований известны: а) Р (А / Н 1) – вероятность узкого таза при благоприятных родах, Р (А / Н 1) = 0,029, б) Р (А / Н 2) – вероятность узкого таза при перинатальной смертности,
Таким образом, риск перинатальной смертности при анатомически узком тазе значительно выше (почти вдвое) среднего риска (4,4 % против 2,5 %).
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1091; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.202 (0.007 с.) |
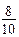 = 0,8 из второй – Р (В) =
= 0,8 из второй – Р (В) =  = 0,4. Вероятность одновременно достать по белому шару из обеих урн –
= 0,4. Вероятность одновременно достать по белому шару из обеих урн – 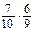 = 0,47 = 47%.
= 0,47 = 47%.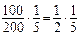 = 0,1 = 10%.
= 0,1 = 10%.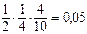 = 5%.
= 5%.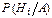 =
= 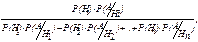 (12)
(12)