
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неоднородные ЛДУ. Метод неопределенных коэффициентов
Рассмотрим линейное неоднородное дифференциальное уравнение n-го порядка
где Для некоторых частных видов функции Замечание. Если
Поставим в соответствие правой части
где Если число, определяемое по правой части, является корнем характеристического уравнения, то говорят, что есть резонанс, в противном случае - нет резонанса. Объединяет частные случаи Очевидно, что частное решение Допустим, что частное решение (1) ищем в виде
то
Рассмотрим три случая: 1. Пусть
и приравняв коэффициенты при одинаковых степенях, получим корректную систему для нахождения 2. Пусть Чтобы получить корректную систему для нахождения В самом деле, многочлен Поэтому, осуществив подстановку (4) с заменой Сократив 3. Пусть Чтобы получить корректную систему для нахождения Действительно, многочлен
Поэтому, осуществив подстановку (4) с заменой Сократив
и приравняв коэффициенты при одинаковых степенях, получим корректную систему для нахождения В следующем примере будут продемонстрированы как различные случаи правых частей, так и принцип суперпозиции. Пример. Найти общее решение Решение. Запишем характеристическое уравнение и решаем его Частное решение по принципу суперпозиции будем искать в виде 1. 2. 3. Таким образом,
Ответ: Найти общее решение: 1.1. 1.5. Задачи для самостоятельного решения: 2.1. 2.8. 2.17. 2.25. Ответы: 2.1. 2.2. 2.4. 2.5. 2.6. 2.8. 2.10. 2.12. 2.14. 2.16. 2.18. 2.20. 2.22. 2.24. 2.25. 2.26.
Пусть дана система дифференциальных уравнений:
Пусть задано начальное состояние системы:
Теорема (Коши для системы дифференциальных уравнений). Если в системе дифференциальных уравнений (1) функции
Замечание. Изменяя в начальных условиях Если в системе (1) правые части Замечание. Если интерпретировать решение системы
Каждое решение системы Следует помнить, что система определяет не только интегральные кривые, но и положительное направление на них, которое соответствует перемещению точки при возрастании Решения автономной системы обладают той особенностью, что перемещение точки Систему ориентированных интегральных кривых называют фазовым портретом системы [1,2]. Пример. Построить фазовый портрет системы Решение. Продифференцировав первое уравнение системы Корни
Поэтому Пусть В полярных координатах получим семейство логарифмических спиралей. Схематический график в таблице 3 (фокус).
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.106.100 (0.038 с.) |
 , (1)
, (1) , …,
, …,  , - постоянные.
, - постоянные.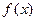 удается найти без интегрирования частное решение неоднородного уравнения (1).
удается найти без интегрирования частное решение неоднородного уравнения (1). - комплексные сопряженные корни характеристического уравнения, то
- комплексные сопряженные корни характеристического уравнения, то 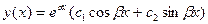 - решение однородного уравнения
- решение однородного уравнения  при любых постоянных
при любых постоянных  ,
,  (общее решение при
(общее решение при  ). Это следует из равенства
). Это следует из равенства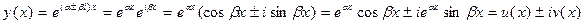 .
. (2)
(2) - обозначает многочлен степени
- обозначает многочлен степени  .
. , где
, где 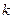 может быть как вещественным числом, так и комплексным.
может быть как вещественным числом, так и комплексным.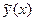 уравнения (1) должно содержать
уравнения (1) должно содержать 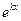 , так как при дифференцировании это выражение сохраняется. Пусть правая часть
, так как при дифференцировании это выражение сохраняется. Пусть правая часть 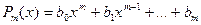 ,
,  , где
, где  - многочлен той же степени, что и
- многочлен той же степени, что и 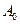 ,
,  ,…,
,…,  - неизвестные. Чтобы найти
- неизвестные. Чтобы найти 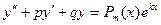 , (3)
, (3) (4)
(4) и
и  - многочлен той же степени
- многочлен той же степени 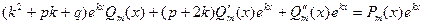
 , т.е. резонансный случай. Тогда
, т.е. резонансный случай. Тогда 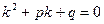 , но
, но  и
и  - многочлен степени
- многочлен степени  , что и
, что и  .
. .
.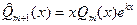 имеет столько же неизвестных
имеет столько же неизвестных 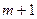 .
. на
на  , получим
, получим 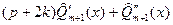 - многочлен той же степени, что и
- многочлен той же степени, что и  .
. и приравняв коэффициенты при одинаковых степенях, получим корректную систему для нахождения
и приравняв коэффициенты при одинаковых степенях, получим корректную систему для нахождения 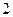 , т.е. по-прежнему резонансный случай. Тогда
, т.е. по-прежнему резонансный случай. Тогда 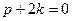 и
и 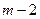 , что и
, что и 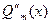 .
. .
. имеет столько же неизвестных
имеет столько же неизвестных  .
.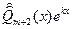 , получим
, получим  - многочлен той же степени, что и
- многочлен той же степени, что и 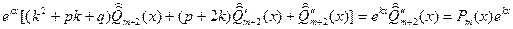
 .
. . Следовательно, общее решение однородного уравнения
. Следовательно, общее решение однородного уравнения  .
.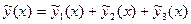 , где
, где  - частные решения соответствующих неоднородных уравнений:
- частные решения соответствующих неоднородных уравнений: , число, соответствующее правой части
, число, соответствующее правой части 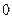 , следовательно, есть резонанс и
, следовательно, есть резонанс и 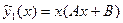 .
.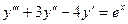 , число, соответствующее правой части
, число, соответствующее правой части  .
. число, соответствующее правой части
число, соответствующее правой части  , следовательно, нет резонанса и
, следовательно, нет резонанса и  .
.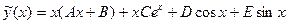 ,
, ,
, ,
, ,
, ,
, 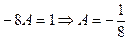 ,
,  ,
,  ,
, .
.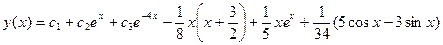 .
. . 1. 2.
. 1. 2. 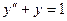 . 1. 3.
. 1. 3. 
 . 1. 4.
. 1. 4. 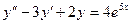 .
. . 1. 6.
. 1. 6. 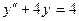 . 1.7.
. 1.7. 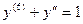 .
. ; 2.2.
; 2.2. 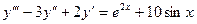 ; 2.3.
; 2.3.  ; 2.4.
; 2.4.  ; 2.5.
; 2.5. 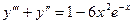 . 2.6.
. 2.6. 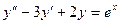 ; 2.7.
; 2.7.  ;
;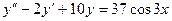 ; 2.9.
; 2.9.  ; 2.10.
; 2.10.  ; 2.11.
; 2.11. 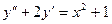 ; 2.12.
; 2.12. 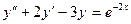 ; 2.13.
; 2.13.  ,
,  ,
,  ; 2.14.
; 2.14. 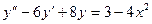 ; 2.15.
; 2.15.  ; 2.16.
; 2.16. 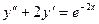 ;
; ; 2.18.
; 2.18.  ; 2.19.
; 2.19.  ,
, 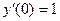 ; 2.20.
; 2.20. 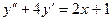 ; 2.21.
; 2.21. 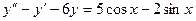 ; 2.22.
; 2.22.  ,
,  ,
,  ; 2.23.
; 2.23.  ; 2.24.
; 2.24. 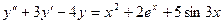 ;
;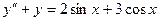 ; 2.26.
; 2.26.  .
. ;
; ; 2.3.
; 2.3.  ;
; ;
; .
. ; 2.7.
; 2.7. 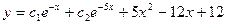 ;
;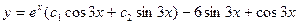 ; 2.9.
; 2.9.  ;
; ; 2.11.
; 2.11.  ;
; ; 2.13.
; 2.13. 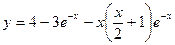 ;
; ; 2.15.
; 2.15.  ;
; ; 2.17.
; 2.17.  ;
;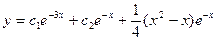 ; 2.19.
; 2.19. 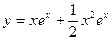 ;
; ; 2.21.
; 2.21.  ;
; ; 2.23.
; 2.23. 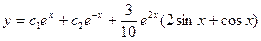 ;
;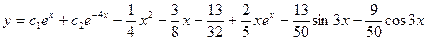 ;
; ;
; .
.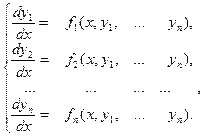 (1)
(1)
 ,
, 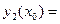
 ,…,
,…, 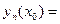
 . (2)
. (2)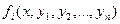 (
( ) удовлетворяют следующим условиям:
) удовлетворяют следующим условиям: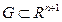 , содержащей точку с координатами
, содержащей точку с координатами  ,
,  по переменным
по переменным  ,
, 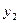 ,…,
,…,  также непрерывны в той же области, то на некотором интервале
также непрерывны в той же области, то на некотором интервале 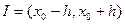 изменения
изменения 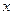 , существует единственная вектор-функция
, существует единственная вектор-функция 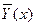
 ,
, 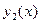 ,…,
,…,  - решение задачи Коши (1), (2).
- решение задачи Коши (1), (2).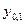 ,
, 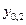 ,…,
,…, 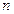 произвольных постоянных.
произвольных постоянных.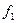 ,….
,…. 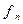 не зависят от независимой переменной, то система называется автономной.
не зависят от независимой переменной, то система называется автономной. ,….
,…. 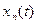 как координаты точки в
как координаты точки в 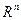 , зависящие от времени,
, зависящие от времени,  ,…,
,…,  - как координаты вектора скорости движущейся точки
- как координаты вектора скорости движущейся точки  , то система называется динамической, функции
, то система называется динамической, функции  .
.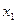 ,….
,….  за время от
за время от  до
до  по траектории системы полностью определяется разностью
по траектории системы полностью определяется разностью 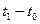 и не зависят от
и не зависят от 
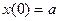 ,
,  (a, b, ¹ 0).
(a, b, ¹ 0). , получим
, получим 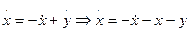 , так как
, так как 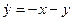 . Из первого уравнения системы находим
. Из первого уравнения системы находим  . Окончательно, исключив
. Окончательно, исключив 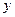 , в итоге получим уравнение второго порядка относительно
, в итоге получим уравнение второго порядка относительно 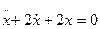 .
.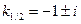 характеристического уравнения
характеристического уравнения  - комплексные сопряженные. Отсюда
- комплексные сопряженные. Отсюда  ,
,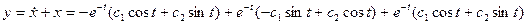 ,
, .
. . Система имеет решение
. Система имеет решение 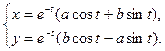
 ,
, 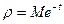 ,
,  ,
,  . Тогда
. Тогда 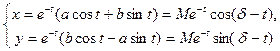 или
или 



