
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 2. Ограниченная последовательность.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Вопрос 1. Числовая последовательность. Примеры. Числовая последовательность – функция натурального аргумента: f(n)=xn Определение: если по некоторому закону каждом натуральному числу n поставлено в соответствие вполне оптимальное число xn, то говорят, что задана числовая последовательность { xn }. Числа x1,x2…,xn - называются членами последовательности, xn – общим членом, или n-м членом данной последовательности. Примеры: 1) 2,4,6..2n,…(монотонная, неограниченная) 2) 1,0,1,0,…(немонотонная, ограниченная) Вопрос 2. Ограниченная последовательность. Послед. xn называется ограниченной, если существуют два числа m,M такие, что xn находится в пределах m≤ xn≤M. -Последовательность {xn} называется ограниченной сверху, если ∃M<+∞ ∀ xn≤M -Последовательность {xn} называется ограниченной снизу, если ∃m>-∞ ∀ xn ≥m. -Последовательность {xn} называется ограниченной, если она одновременно ограничена и сверху и снизу. Вопрос 3. Предел числовой последовательности. Определение: число А называется пределом последовательности { аn }, если для любого положительного числа ε>0 найдется такой N(номер, зависящий от ε), начиная с которого будет выполняться неравенство: |х n-а|< ε Предел числовой последовательности обозначается Последовательность, имеющая предел, называется сходящейся, а в противном случае – расходящейся. Смысл определения предела последовательности состоит в том, что для достаточно больших n члены последовательности { аn } как угодно мало отличаются от числа А.. Последовательность всходящая, если у нее есть предел. Вопрос 4. Единственность предела сходящейся последовательности. Теорема: Если последовательность сходится, то у нее существует единственный предел. Доказательство методом от противного: Пусть у сходящейся последовательности существует 2 предела.
Пусть N = max{ N 1, N 2 }, тогда при всех n > N имеем
И, поскольку ε является как угодно малым положительным числом, как единственно возможное, имеем a = b. Вопрос 5. Ограниченность сходящейся последовательности. Если последовательность имеет конечный предел, то последовательность ограничена. Если последовательность сходится, то она ограничена. Доказательство: пусть последовательность сходится, то есть Пусть M=max{ m=min{ Значит, по определению последовательность Ограниченность последовательности является необходимым условием сходимости, но не является достаточным. Существуют ограниченные последовательности, которые не являются сходящимися. Например, Пусть последовательность ограничена, будет ли она сходящейся? – Ограниченная сходимость следует не всегда.
Вопрос 6. Свойства пределов, связанные с арифметическими действиями (для последовательности) {xn;n=1,2…} {yn;n=1,2…} 1) xn ±yn 2) Cxn, c- const 3) xn *yn 4)
Вопрос 7. Переход к пределу в неравенствах Пусть Тогда Док-во: предложим противное: по определению пределов: (*) (**)
Вопрос 8. Теорема о двух милиционерах
тогда Вопрос 11. Предел функции в точке Пусть функция y=f(x) задана в некоторой окрестности точки х0, кроме, может быть, самой точки х0. Определение: Число А называется пределом функции f(x) при х стремящемся к х0 (или в точке х0), если для любого, даже сколь угодно малого положительного числа ε>0, найдется такое положительное число N>0(зависящее от ε, т.е. N(ε)), что для всех х, не равных х0 и удовлетворяющее условию Этот предел функции обозначается Смысл определения предела функции f(x) в точке х0 состоит в том, что для всех значений х, достаточно близких к х0, значение функции f(x) как угодно мало отличается от числа А(по абсолютной величине). Вопрос 12. Свойства предела, связанного с арифметическими действиями(для функций) Пусть последовательность xn и yn сходящиеся:
1) 2) 3) 4) Правило: При вычислении пределов в произведении одну бесконечно малую величину можно заменять на ей эквивалентную бесконечно малую.
Вопрос 17. Непрерывность функции в точке. Различные определения. Определение 1. Функция называется непрерывной в точке х0, если предел при х→х0 сущствует и равен значению функции в этой точке.
Определение непрерывности функции в точке х0 может быть записано и так:
т.е. для непрерывной функции возможна перестановка символов предела и функции. Определение 2.
Если ∆х→0, то ∆у→0. Точка х0 наз. точкой разрыва функции, если эта функция в данной точке не явл. непрерывн.Различ. точки разрыва 1ого рода(когда существуют конечные односторонние пределы функции слева и справа при х→х0, не равные др. др.) и 2ого рода(хотя бы один из односторон. пределов слева или справа равен бесконечности либо не сущ.) Свойства функций, непрерывных в точке: 1) Если функции f(x) и g(x) непрерывны в точке х0, то их сумма, произведение и частное являются функциями, непрерывными в точке х0. 2) Если функция y=f(x) непрерывна в точке х0 и f(x0)>0, то существует такая окрестность точки х0, в которой f(x)>0. 3) Если функция y=f(u) непрерывна в точке u0 , а функция u=g(x) непрерывна в точке u0=g(x0), то сложная функция y=f(g(x)) непрерывна в точке х0 Вопрос 30. Теорема Ролля Пусть функция f(x) дифференцируема внутри интервала (a;b)- непрерывна на сегменте и на f(a)=f(b) (на концах отрезка принимает равные значения)найдется такая точка, в которой производная равна 0. f’(c)=0 c ∈ (a;b) Геометрический смысл теоремы: Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс; в этой точке производная и будет равняться 0. Проиллюстрируем эту теорему геометрически:
f’(x)=0
f(x)- не является константой. f(x)≠f(a) Пусть f(x)>f(a), значение на концах функции равны Пусть f(x)>f(a), по условию f(a)=f(b)=>f(x)>f(b) f’(c)=0
Теорема Коши. Пусть f(x) и g(x) непрерывны на отрезке [a;b] и дифференцируема на интервале (a;b), тогда справедлива следующая формула:
Экстремум функции - в точке х0 у функции будет max, если в окрестности точки х0 f(x0)>f(x) - и min, если для всех х из окрестности f(x0)<f(x).
Вопрос 37. Необходимое и достаточное условие экстремума.
-Необходимое условие экстремума: Пусть в точке х0 у функции будет экстремум, тогда необходимо, чтобы производная в этой точке была равна 0 или не существовала. Доказательство: Для определенности положим, что в точке х, равной х0, будет максимум, т.е существует такая окрестность этой точки, в которой f(x0)>f(x). Тогда функция в точке х=х0 не может не возрастать, не убывать.
y=x3 y’=3x2 y’(0)=0
- Достаточное условие экстремума. Пусть в точке х0 производная =0 и в окрестности этой точки меняет знак, тогда в этой точке будет экстремум, а если при переходе через точку х0 производная меняет свой знак с + на -, то точка х0 есть точка максимума, а если с – на +, то точка минимума.
Вопрос 47. Таблица интегралов.
Таблица интегралов проверяется дифференцированием. Вопрос 60.Числовые ряды Числовым рядом называется сумма Признак Коши. Пусть существует предел 1)q<1- ряд сходится 2)q>1-ряд расходится 3)q=1- ничего сказать нельзя(признак не работает) Доказательство: Для любого положения числа ε(∀ε>0) мы имеем 1) q<1
т.к. ε – любое число, его можно взять таким, что q+ε=q1<1 an<a1n
2) q>1 За счет выбора ε можно q-ε>1 q-ε=q2 qn>q2n – расходится Признак Даламбера. Пусть существует 1)q<1 –ряд сходится 2)q>1-ряд расходится 3) q=1- нужны дополнительные сведения. Доказательство: (∀ε>0)
1) q<1, также за счет выбора ε можно q+ε=q<1 an+1<anq1<an-1q2...<a1qn но
2) q>1 аналогично, как признак Коши. Признак Лейбница Если члены знакочередующегося ряда убывают по абсолютной величине u1>u2>u3>…>un>… и предел его общего члена при n→∞ равен 0, т.е.
1) строгое знакочередование
Sn=ln2 2) Рассмотрим ряд из модулей
Вопрос 1. Числовая последовательность. Примеры. Числовая последовательность – функция натурального аргумента: f(n)=xn Определение: если по некоторому закону каждом натуральному числу n поставлено в соответствие вполне оптимальное число xn, то говорят, что задана числовая последовательность { xn }. Числа x1,x2…,xn - называются членами последовательности, xn – общим членом, или n-м членом данной последовательности. Примеры: 1) 2,4,6..2n,…(монотонная, неограниченная) 2) 1,0,1,0,…(немонотонная, ограниченная) Вопрос 2. Ограниченная последовательность. Послед. xn называется ограниченной, если существуют два числа m,M такие, что xn находится в пределах m≤ xn≤M. -Последовательность {xn} называется ограниченной сверху, если ∃M<+∞ ∀ xn≤M -Последовательность {xn} называется ограниченной снизу, если ∃m>-∞ ∀ xn ≥m. -Последовательность {xn} называется ограниченной, если она одновременно ограничена и сверху и снизу.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 3810; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 или аn→А при n→∞.
или аn→А при n→∞.
 a ≠ b.
a ≠ b. ,
, 


 . Тогда по определению выполняется
. Тогда по определению выполняется  . Пусть
. Пусть  =1, тогда
=1, тогда  .
. }
} }, тогда
}, тогда  .
. является ограниченной.
является ограниченной. .
. неограниченная
неограниченная ограниченная
ограниченная
 и
и  ;
;  ,
,
 >
>  <
<  ;
;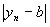 <
< 
 <
< 
 будут выполнены (*) и (**)
будут выполнены (*) и (**) <
< 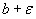 <
<  <
< 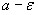 <
<  ;т.е
;т.е ,что противоречит условию значит
,что противоречит условию значит  не верно,а
не верно,а 



 , выполняется неравенство f(x) –A< ε.
, выполняется неравенство f(x) –A< ε. или
или  при
при 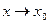 .
.
 , следовательно справдливо:
, следовательно справдливо:


 , если
, если  (предел частного = частному пределов, если предел yn отмечен на прямой)
(предел частного = частному пределов, если предел yn отмечен на прямой)

 - приращение функции.
- приращение функции. Функция y=f(x) называется непрерывной в точке х0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
Функция y=f(x) называется непрерывной в точке х0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
 Найдет такая точка С, в которой касательная будет горизонтальна в этой точке производная равна 0.
Найдет такая точка С, в которой касательная будет горизонтальна в этой точке производная равна 0. Доказательство: Пусть функция f(x) – постоянна х ∈ (a;b), тогда значение производной во всех точках равно 0.
Доказательство: Пусть функция f(x) – постоянна х ∈ (a;b), тогда значение производной во всех точках равно 0.
 , где
, где  - какая-то точка из интервала (a;b)
- какая-то точка из интервала (a;b)






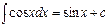









 , an- общий член ряда.
, an- общий член ряда. , тогда:
, тогда:

 - это геометрическая прогрессия со знаком <1 => сходится, поэтому по признаку сравнения исходный ряд сходится.
- это геометрическая прогрессия со знаком <1 => сходится, поэтому по признаку сравнения исходный ряд сходится. 
 , тогда
, тогда
 - сходится => исходный ряд тоже сходится.
- сходится => исходный ряд тоже сходится. , то ряд сходится, а его сумма не превосходит первого члена: S≤u1.
, то ряд сходится, а его сумма не превосходит первого члена: S≤u1. и
и  2bn 4bn ↓0
2bn 4bn ↓0 bn→0 n→∞
bn→0 n→∞

 - расходится, поэтому сходимость у исходного ряда условная.
- расходится, поэтому сходимость у исходного ряда условная.


