
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гетероскедастичность. Метод Спирмена. ⇐ ПредыдущаяСтр 2 из 2
Гетероскедастичность – свойство оценок коэффициентов регрессии, когда они зависят от свойств случайного члена. При использовании теста Спирмена предполагается, что дисперсия отклонения будет или увеличиваться, или уменьшаться с увеличением значений X. Поэтому для регрессии, построенной по методу наименьших квадратах, абсолютные величины отклонений ei и значения xi объясняющей переменной X будут коррелированы. Значения xi и ei ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции. Доказано, что если коэффициент корреляции ρx,|e| для генеральной совокупности равен нулю, то статистика имеет t-распределение Стьюдента с числом степеней свободы v = n - 2. Следовательно, если наблюдаемое значение t-статистики, вычисленное по формуле представленной выше, превышает tкр = tα/2,n-2 (определяется по таблице критических значений распределения Стьюдента), то нужно отклонить гипотезу о равенстве нулю коэффициента корреляции ρx,e, следовательно, и об отсутствии гетероскедастичности. В противном случае гипотеза об отсутствии гетероскедастичности принимается.
8. Классическая линейная регрессионная модель и ее предпосылки.
Классический подход к оцениванию параметров линейной модели основан на методе наименьших квадратов (МНК). Вычисление оценок МНК не требует, вообще-то говоря, введения каких-либо дополнительных гипотез. Сам метод часто рассматривают как способ «разумного» выравнивания эмпирических данных. Относительно оценок МНК можно сделать следующие выводы: 1. Оценки МНК являются функциями от выборки, что позволяет их легко рассчитывать. 2.Оценки МНК являются точечными оценками теоретических коэффициентоврегрессии,т.е. M(ai)=αi i=0,k 2 3.Эмпирическое уравнение регрессии строится таким образом, что ∑ ei = 0 и среднее значение отклонений будет равно 0. В то же время оценки a = (a0, a1, a2,....ak), вычисленные по МНК, не позволяют сделать вывод, насколько близки найденные значения параметров к своим теоретическим прототипам α = (α0,α1,.....αk) и насколько надежны найденные оценки. Поэтому для оценки адекватности модели и ее прогностической способности необходимо введение дополнительных предположений.
В классической модели линейной регрессии делаются следующие теоретические ограничения на модель: • Факторные (объясняющие) переменные (X1,X2,.....Xk) являются неслучайными величинами. • Ни одна из объясняющих переменных не является строгой линейной функцией других объясняющих переменных. Следовательно, ранг матрицы X равен k + 1 < n, где k – число факторных переменных, n.-число наблюдений Свойства оценок МНК напрямую зависят от свойств случайного членаε. Покажем это на примере множественной регрессии: Y = X ⋅ A + ε
Сформируем основные предпосылки:
1. Нулевое математическое ожидание ошибок; 2. Диагональность ковариационной матрицы ошибок; 3. Отсутствие гетероскедастичности в модели.
Нарушение любой из этих предпосылок ведет к искажению полученных результатов. Можно не обнаружить существующую зависимость или построить ложную модель. Поэтому, за кажущейся простотой метода скрывается целый комплекс проблем, неочевидных на первый взгляд.
9. Коэффициент эластичности. Средний и точечный коэффициент эластичности линейной, гиперболической, степенной и показательной функции.
Эластичность показывает, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней
Средний коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего среднего уровня, если факторная переменная х изменится на 1 % относительного своего среднего уровня
Общая формула для расчёта коэффициента эластичности для среднего значения
Где.
– значение функции у при среднем значении факторной переменной х. Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.
Для показательной функции вида:
средний коэффициент эластичности
средний коэффициент эластичности определяется по формуле:
Точечные коэффициенты эластичности характеризуются тем, что эластичность функции зависит от заданного значения факторной переменной х1. Точечный коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего значения в точке х1, если факторная переменная изменится на 1 % относительно заданного уровня х1.
Для линейной функции вида: yi=β0+β1xi,
В знаменателе данного
Для показательной функции вида:
точечный коэффициент эластичности определяется по формуле:
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.200.35 (0.011 с.) |
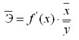 величины:
величины: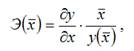 факторной переменной х:
факторной переменной х: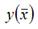
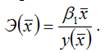 Для линейной функции вида: yi=β0+β1xi, средний коэффициент эластичности определяется по формуле:
Для линейной функции вида: yi=β0+β1xi, средний коэффициент эластичности определяется по формуле: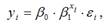
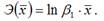 определяется по формуле:
определяется по формуле: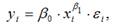
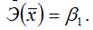 Для степенной функции вида:
Для степенной функции вида: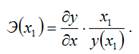 Общая формула для расчёта коэффициента эластичности для заданного значения х1факторной переменной х:
Общая формула для расчёта коэффициента эластичности для заданного значения х1факторной переменной х: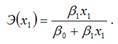 точечный коэффициент эластичности определяется по формуле:
точечный коэффициент эластичности определяется по формуле: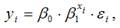 показателя стоит значение линейной функции в точке х1.
показателя стоит значение линейной функции в точке х1.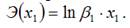
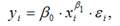 точечный коэффициент эластичности определяется по формуле:
точечный коэффициент эластичности определяется по формуле: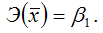 Для степенной функции вида:
Для степенной функции вида:


