Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойство2. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от слагаемых.Стр 1 из 6Следующая ⇒
Доказательство. Свойство3. Если на отрезке [a,b], где а<b, функции f(x) и j(х) удовлетворяют условию Доказательство. Рассмотрим разность
Каждая разность Сл-но, неотрицательно каждое слагаемое, неотрицательны вся сумма и весь предел. Свойство4. Если m и М – наименьшее и наибольшее значения функции f(x) на отрезке [a,b] и
Доказательство. По условию
Подставляя 2 последние выражения в неравенство получаем исходное неравенство. Свойство5 (теорема о среднем). Если функция f(x) непрерывна на отрезке [a,b], то на этом отрезке найдется такая точка Доказательство. Пусть a<b, m – наименьшее значение функции, М – наибольшее значение f(x) на отрезке [a,b]. Тогда получаем
Так как функция непрерывна на отрезке, то она принимает все промежуточные значения, заключенные между m и М. Следовательно, при некотором значении Примечание автора. Доказательство приведено и в одном из следующих вопросов. Свойство6. Для любых трех чисел a,b,c справедливо равенство Доказательство. Допустим сначала, что Так как предел интегральной суммы не зависит от способа разбиения отрезка, будем разбивать отрезок так, чтобы точка с была точкой деления. Тогда Переходя к пределу при Если Поэтому имеем Аналогично доказывается это свойство при любом взаимном расположении трех точек. Свойство определенного интеграла – теорема о среднем. Обобщенная теорема о среднем. Теорема. Если функция f(x) непрерывна на отрезке [a,b], то на этом отрезке найдется такая точка Доказательство. Пусть a<b, m – наименьшее значение функции, М – наибольшее значение f(x) на отрезке [a,b]. Тогда получаем
Так как функция непрерывна на отрезке, то она принимает все промежуточные значения, заключенные между m и М. Следовательно, при некотором значении Геометрический смысл теоремы. Величина определенного интеграла при f(x) ³ 0 равна площади прямоугольника, имеющего высоту f(c) и основание (b–a). Обобщенная теорема о среднем. Если функции f(x) и j(x) непрерывны на отрезке
[a,b], и функция j(х) знакопостоянна на нем, то на этом отрезке существует точка e, такая, что
Замена переменной в определенном интеграле. Теорема. Пусть f(x) – непрерывная функция на отрезке Если выполняются условия:
Доказательство.
Из равенства правых частей следует равенство левых. Интегрирование по частям в определенном интеграле. Теорема. Если функции u и v непрерывно дифференцируемы на отрезке [a,b], справедливо равенство Доказательство. Так как функции u и v дифференцируемы, получаем
Определенный интеграл с переменным верхним пределом. Определение. Пусть функция f непрерывна на отрезке [a,b]. Функция Теорема. Функия F непрерывна на отрезке [a,b]. Доказательство. Пусть Пусть М-верхняя граница f(x), тогда при х>x0 получаем
Теорема Барроу. Производная от интеграла от непрерывной функции по переменному верхнему пределу существует и равна значению подынтегральной функции в точке, равной верхнему пределу. Вторая формулировка. Пусть х0 – точка непрерывности функции, тогда существует Доказательство. Можно выбрать
Формула Ньютона-Лейбница.
Примечание автора. Необходимо отметить, что ни у Ньютона, ни у Лейбница не было такой формулы в точном виде. Важно именно то, что именно Лейбниц и Ньютон впервые установили связь между интегрированием и дифференцированием, позволяющую создать правило для вычисления определенных интегралов. Доказательство. Пусть F(x) – некоторая первообразная от f(x). Функция Это равенство при соответствующем выборе С* справедливо при всех значениях х, т.е. является тождеством. Для определения постоянного С* положим в этом тождестве х=а, тогда
Также отметим, что разность Интеграл ошибок. Интеграл определяется формулой: Укажем некоторые свойства функции Ф(х): 1.Функция определена при всех значениях х. 2. Ф(0)=0. 3. 4. Функция монотонно возрастает на 5. Функция нечетная, График функции. Примечание автора. Обязательна графическая иллюстрация.
Составлены подробные таблицы значений этой функции.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.222.47 (0.013 с.) |


 то
то 
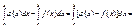



 то
то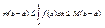

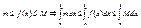


 что справедливо равенство:
что справедливо равенство: 
 Отсюда
Отсюда  где
где 
 будет
будет  то есть
то есть 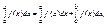 если все эти три интеграла существуют.
если все эти три интеграла существуют.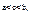 и составим интегральную сумму для функции f(x) на отрезке [a,b].
и составим интегральную сумму для функции f(x) на отрезке [a,b].
 получим исходное соотношение.
получим исходное соотношение. на основании доказанного
на основании доказанного 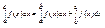 или
или 

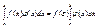
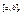 а
а 


 и
и 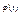 непрерывны на отрезке
непрерывны на отрезке  а
а  определена на этом отрезке, то
определена на этом отрезке, то


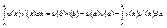

 Это можно записать как
Это можно записать как 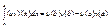 Отсюда,
Отсюда,  - интеграл с переменным верхним пределом.
- интеграл с переменным верхним пределом. тогда
тогда 
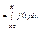
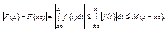 Или при х>x0:
Или при х>x0: Следовательно,
Следовательно, 
 Т.е. функция непрерывна в точке х0.
Т.е. функция непрерывна в точке х0. или, иначе,
или, иначе, 
 так, что на интервале
так, что на интервале  функция будет непрерывна. Возьмем произвольное значение х из данного интервала.
функция будет непрерывна. Возьмем произвольное значение х из данного интервала.  с лежит между х и х0.
с лежит между х и х0. Следовательно,
Следовательно, 

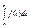 есть также первообразная от f(x). Две любые первообразные от данной функции отличаются на константу С. Тогда получаем
есть также первообразная от f(x). Две любые первообразные от данной функции отличаются на константу С. Тогда получаем 
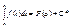

 Следовательно,
Следовательно,  Полагая х=b, получаем формулу Ньютона-Лейбница.
Полагая х=b, получаем формулу Ньютона-Лейбница. не зависит от выбора первообразной F, так как константа при вычитании все равно уничтожается.
не зависит от выбора первообразной F, так как константа при вычитании все равно уничтожается.