
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Удаление элемента из начала списка
PROCEDURE DEL_BEG_LIST (VAR FIRST: EL); VAR P: EL; ANSWER: STRING; BEGIN IF FIRST <> NIL THEN BEGIN { СПИСОК НЕ ПУСТ } WRITELN ('ВЫ ХОТИТЕ УДАЛИТЬ ПЕРВЫЙ ЭЛЕМЕНТ?(ДА/НЕТ) '); READLN (ANSWER); IF ANSWER = 'ДА' THEN BEGIN P:=FIRST; IF P^.NEXT = NIL THEN {В СПИСКЕ ОДИН ЭЛЕМЕНТ } BEGIN DISPOSE (P); {УНИЧТОЖЕНИЕ ЭЛЕМЕНТА} FIRST:=NIL; {СПИСОК СТАЛ ПУСТЫМ } END ELSE BEGIN P:= FIRST;{АДРЕС УДАЛЯЕМОГО ЭЛЕМЕНТА } FIRST:=FIRST^.NEXT; {АДРЕС НОВОГО ПЕРВОГО ЭЛЕМЕНТА} DISPOSE(P); {УДАЛЕНИЕ БЫВШЕГО ПЕРВОГО ЭЛЕМЕНТА } END; END END 18. Бинарное дерево. Основные определения и понятия. Бинарный поиск по дереву. Формирование бинарного дерева этим методом Бинарное (двоичное) дерево (binary tree) – древовидная структура данных, в которой каждый узел имеет не более двух потомков (детей). Бинарное дерево [др. источник] – это упорядоченное дерево, каждая вершина которого имеет не более двух поддеревьев, причем для каждого узла выполняется правило: в левом поддереве содержатся только ключи, имеющие значения, меньшие, чем значение данного узла, а в правом поддереве содержатся только ключи, имеющие значения, большие, чем значение данного узла. Бинарное дерево является рекурсивной структурой, поскольку каждое его поддерево само является бинарным деревом и, следовательно, каждый его узел в свою очередь является корнем дерева. Узел дерева, не имеющий потомков, называется листом. То есть двоичное дерево либо является пустым, либо состоит из данных и двух поддеревьев (каждое из которых может быть пустым). Очевидным, но важным для понимания фактом является то, что каждое поддерево в свою очередь тоже является деревом.
У вершины n=(data, left, right) есть два ребёнка (левый и правый) left и right и, соответственно, два поддерева (левое и правое) с корнями left и right. Свойство. Строго бинарное дерево с n листами всегда содержит 2n-1 узлов. Уровень узла в бинарном дереве: уровень корня всегда равен нулю, а далее номера уровней при движении по дереву от корня увеличиваются на 1 по отношению к своему непосредственному предку. Глубина бинарного дерева - это максимальный уровень листа дерева, что равно длине самого длинного пути от корня к листу дерева. Полное бинарное дерево уровня n - это дерево, в котором каждый узел уровня n является листом, и каждый узел уровня меньше n имеет непустые левое и правое поддеревья
Почти полное бинарное дерево - это бинарное дерево, для которого существует неотрицательное целое k такое, что: 1) Каждый лист в дереве имеет уровень k или k+1. 2) Если узел дерева имеет правого потомка уровня k+1, тогда все его левые потомки, являющиеся листами, также имеют уровень k+1. Упорядоченные бинарные деревья - это деревья, в которых для каждого узла Х выполняется правило: в левом поддереве - ключи, меньшие Х, в правом поддереве - большие или равные Х. Построение бинарного дерева. Двоичное дерево поиска.
Этот принцип используется и при формировании двоичного дерева, и при поиске в нем элементов. Обратить внимание: поиск места подключения очередного элемента всегда начинается с корня. Пример: 20, 10, 35, 15, 17, 27, 24, 8, 30. Поиск элемента в бинарном дереве. При поиске элемента с некоторым значением признака происходит спуск по дереву, начиная от корня, причем выбор ветви следующего шага - направо или налево согласно значению искомого признака - происходит в каждом очередном узле на этом пути. При поиске элемента результатом будет либо найденный узел с заданным значением признака, либо поиск закончится листом с «нулевой» ссылкой, а требуемый элемент отсутствует на проделанном по дереву пути. Если поиск был проделан для включения очередного узла в дерево, то в результате будет найден узел с пустой ссылкой (пустыми ссылками), к которому справа или слева в соответствии со значением признака и будет присоединен новый узел. Двоичное дерево поиска можно определить так: − Двоичное дерево состоит из узлов (вершин) — записей вида (data, left, right), где data — некоторые данные привязанные к узлу, left и right — ссылки на потомков. − Данные (data) обладают ключом (key) на котором определена операция сравнения " меньше ". В конкретных реализациях это может быть пара (key, value). − Для любого узла X выполняются свойства дерева поиска:
key[left[X]] < key[X] ≤ key[right[X]], т. е. ключи данных родительского узла больше ключей данных левого сына и нестрого меньше ключей данных правого. Основные операции в двоичном дереве поиска: FIND (K) — поиск узла, в котором хранится пара (key, value) с key = K. INSERT (K,V) — добавление в дерево пары (key, value) = (K, V). REMOVE (K) — удаление узла, в котором хранится пара (key, value) с key = K.
Бинарное дерево. Основные операции с бинарными деревьями. Способы обхода бинарного дерева. Варианты поиска по бинарному дереву Бинарное (двоичное) дерево (binary tree) – древовидная структура данных, в которой каждый узел имеет не более двух потомков (детей). Бинарное дерево [др. источник] – это упорядоченное дерево, каждая вершина которого имеет не более двух поддеревьев, причем для каждого узла выполняется правило: в левом поддереве содержатся только ключи, имеющие значения, меньшие, чем значение данного узла, а в правом поддереве содержатся только ключи, имеющие значения, большие, чем значение данного узла. Бинарное дерево является рекурсивной структурой, поскольку каждое его поддерево само является бинарным деревом и, следовательно, каждый его узел в свою очередь является корнем дерева. Узел дерева, не имеющий потомков, называется листом. То есть двоичное дерево либо является пустым, либо состоит из данных и двух поддеревьев (каждое из которых может быть пустым). Очевидным, но важным для понимания фактом является то, что каждое поддерево в свою очередь тоже является деревом.
У вершины n=(data, left, right) есть два ребёнка (левый и правый) left и right и, соответственно, два поддерева (левое и правое) с корнями left и right. Свойство. Строго бинарное дерево с n листами всегда содержит 2n-1 узлов. Уровень узла в бинарном дереве: уровень корня всегда равен нулю, а далее номера уровней при движении по дереву от корня увеличиваются на 1 по отношению к своему непосредственному предку. Глубина бинарного дерева - это максимальный уровень листа дерева, что равно длине самого длинного пути от корня к листу дерева. Полное бинарное дерево уровня n - это дерево, в котором каждый узел уровня n является листом, и каждый узел уровня меньше n имеет непустые левое и правое поддеревья Почти полное бинарное дерево - это бинарное дерево, для которого существует неотрицательное целое k такое, что: 1) Каждый лист в дереве имеет уровень k или k+1. 2) Если узел дерева имеет правого потомка уровня k+1, тогда все его левые потомки, являющиеся листами, также имеют уровень k+1. Упорядоченные бинарные деревья - это деревья, в которых для каждого узла Х выполняется правило: в левом поддереве - ключи, меньшие Х, в правом поддереве - большие или равные Х. Построение бинарного дерева. Двоичное дерево поиска.
Этот принцип используется и при формировании двоичного дерева, и при поиске в нем элементов. Обратить внимание: поиск места подключения очередного элемента всегда начинается с корня. Пример: 20, 10, 35, 15, 17, 27, 24, 8, 30. Основные операции в двоичном дереве поиска:
FIND (K) — поиск узла, в котором хранится пара (key, value) с key = K. INSERT (K,V) — добавление в дерево пары (key, value) = (K, V). REMOVE (K) — удаление узла, в котором хранится пара (key, value) с key = K.
− в симметричном порядке INFIX _TRAVERSE (f) — обойти всё дерево, следуя порядку (левое поддерево, вершина, правое поддерево). − в прямом порядке PREFIX _TRAVERSE (f) — обойти всё дерево, следуя порядку (вершина, левое поддерево, правое поддерево). − в обратном порядке POSTFIX _TRAVERSE (f) — обойти всё дерево, следуя порядку (левое поддерево, правое поддерево, вершина) Поиск элемента в бинарном дереве. При поиске элемента с некоторым значением признака происходит спуск по дереву, начиная от корня, причем выбор ветви следующего шага - направо или налево согласно значению искомого признака - происходит в каждом очередном узле на этом пути. При поиске элемента результатом будет либо найденный узел с заданным значением признака, либо поиск закончится листом с «нулевой» ссылкой, а требуемый элемент отсутствует на проделанном по дереву пути. Если поиск был проделан для включения очередного узла в дерево, то в результате будет найден узел с пустой ссылкой (пустыми ссылками), к которому справа или слева в соответствии со значением признака и будет присоединен новый узел.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 692; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.42.168 (0.012 с.) |
 Каждый узел в дереве задаёт поддерево, корнем которого он является.
Каждый узел в дереве задаёт поддерево, корнем которого он является.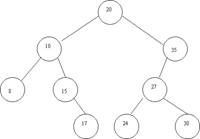 Правило построения двоичного дерева поиска: элементы, у которых значение некоторого признака меньше, чем у корня, всегда включаются слева от некоторого поддерева, а элементы со значениями, большими, чем у корня - справа.
Правило построения двоичного дерева поиска: элементы, у которых значение некоторого признака меньше, чем у корня, всегда включаются слева от некоторого поддерева, а элементы со значениями, большими, чем у корня - справа. Способы обхода бинарного дерева (TRAVERSE).
Способы обхода бинарного дерева (TRAVERSE).


