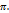Исследование функции 2х перемен-ых на локальный экстремум.

Необходимое условие локального экстремума дифференцируемой функции: Если(x₀ ,y₀)-точка экстремума функции f, то x_0,y₀)=0 и (x_0,y₀)=0 Достаточные условия локального экстремума дважды дифференцируемой функции Обозначим Если D > 0, A > 0, то(x0,y0) - точка минимума. Если D > 0, A < 0, то (x0,y0) - точка максимума. Если D < 0, экстемума в точке(x0,y0) нет. Если D = 0, необходимы дополнительные исследования.

 

45.Мнимая единица и комплексные числа. Комплексная плоскость и бесконечно большое комплексное число.Опр.1 Комплексным числом z называется выражение вида z=х+iу, где х и у — действительные числа, a i — так называемая мнимая единица, i²=-1. Если x=0, то число 0+iy=iy называется чисто мнимым; если у=0, то число х+i0=х отождествляется с действительным числом х, а это означает, что множество R всех действительных чисел является подмножеством множества С всех комплексных чисел, т. e. RÌС. Мнимая единица — это число, квадрат которого равен −1. Т.е. i — это одно из решений уравнения Число х называется действительной частью комплексного числа z и обозначается х=Re z, а у — мнимой частью z, у = Im z. Два комплексных числа z₁=x₁+iy₁ и z₂=х₂+iy₂ называются равными (z₁=z₂) тогда и только тогда, когда равны их действительные части и равны их мнимые части: х₁=х₂, y₁=у₂. В частности, комплексное число z=х+iy равно нулю тогда и только тогда, когда х=у=0. Понятия «больше» и «меньше» для комплексных чисел не вводятся. Два комплексных числа z=х+iy и z=х-iy, отличающиеся лишь знаком мнимой части, называются сопряженными. Опр2. Координатная плоскость, каждая точка которой отождествлена с комплексным числом, называется комплексной плоскостью. Ось абсцисс Ох называется действительной осью, Ось ординат Оу называется мнимой осью. Замеч. Существует взаимно однозначное соответствие между точками координатной плоскости и их радиус-векторами. Поэтому также существует взаимно однозначное соответствие и между всеми комплексными числами и радиус-векторами соответствующих точек комплексной плоскости. Итак, чтобы изобразить комплексное число z точкой на комплексной плоскости нужно записать его в алгебраической форме записи, найти его действительную и мнимую части и построить в ПДСК на этой плоскости точку, абсцисса которой равна действительной части, а ордината – мнимой части данного комплексного числа z: z=a+bi↔z(a,b) ↔Ozвектор, где векторOz является радиус-вектором точки z.

 

46. Алгебраическая, тригонометрическая и показательная формы комп-го числа. 1.Пусть x и y – обычные числа. Число вида z=x+iy называется комплексным числом в алгебраической форме. x называют вещественной или действительной частью числа z и обозначают так:x=Re(z); y называют мнимой частью числа z и обозначают так:x=lm(z).Число Ẑ=x-iy. называют комплексно сопряженным числу z. Действует следующее общее правило: «чтобы получить число, комплексно сопряженное данному, надо в нем заменить i на –i». 2. С геометрической интерпретацией связана и еще одна форма записи комплексных чисел, называемая тригонометрической формой их записи. Соединим точку (x, y) с началом координат отрезком прямой. Длина этого отрезка r называется модулем комплексного числа z и обозначается | z | или mod(z). Угол j, который этот отрезок образует с осью ОХ, называется аргументом комплексного числа z и обозначается arg(z).Из рисунка ясно, что имеют место соотношения - Эта форма и получила название комплексного числа в тригонометрической форме. 3. Однаиз важнейших формул математического анализа – формула Эйлера – имеет вид С учетом тригонометрической формы комплексного числа его теперь можно представить в виде или, с учетом того, что аргумент определяется с точностью до 2p, Эта форма записи помогает, например, определить логарифм комплексного числа

 

47. Операции над комплесными числами. Логарифм компле-го числа. 1.Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда a=c и b= d. 2.Суммой двух комплексных чисел a + ib и c + id называется комплексное число a + c + i(b + d). 3.Произведением двух комплексных чисел a+ ib и c+id назы-ся комп-ное число ac–bd + i(ad +bc). Эти операции обладают следующими свойствами:

1. Коммутативность сложения: z₁+ z₂= z₂+z₁, для любых z_1, z₂

2. Ассоциативность сложения: (z1 + z2) + z3 = z1 + (z2 + z3), для любых z_1, z₂

3. Существует такое число z = 0, которое обладает свойством z + 0 = z, для любого z .

4. Для любых двух чисел z1 и z2 существует такое число z, что z1 + z = z2. Такое число z называется разностью двух комплексных чисел и обозначается z = z2 – z1.

5. Коммутативность умножения: z1z2 = z2z1, для любых z_1, z₂

6. Ассоциативность умножения: (z1z2)z3 = z1(z2z3), для любых z_1,z_2,z₃

7. Дистрибутивность сложения относительно умножения: z1(z2 + z3) = z1z2 + z1z3, для любых z_1,z_2,z₃ 8. Для любого комплексного числа z:z · 1 = z. 9. Для любых двух чисел z₁иz₂существует такое число z, что z₁*z=z₂. Такое число z называется частным двух комплексных чисел и обозначается z=z₂\z₁. Деление на 0 невозможно.

Для комплексных чисел логарифм определяется так же, как вещественный. На практике используется почти исключительно натуральный комплексный логарифм, который обозначается Ln zи определяется как решение w уравнения e^w=z. Комплексный нуль не имеет логарифма, поскольку комплексная экспонента не принимает нулевого значения. Ненулевое z можно представить в показательной форме. Kомплексный логарифм Ln z существует для любого z , и его вещественная часть определяется однозначно, в то время как мнимая часть имеет бесконечное множество значений, различающихся на целое кратное 2

 

48.Многочлены.Разложение многочленов на множители. Многочленом называется сумма одночленов. Если все одночлены в многочлене приведены к стандартному виду, то говорят, что это многочлен стандартного вида. Алгебраическое выражение, не содержащее операции деления и извлечения корня (такое выражение называется целым), всегда может быть приведено к многочлену стандартного вида. Степенью многочлена называется наибольшая из степеней его слагаемых.Имеет смысл говорить о разложении многочлена на множители, если его степень не ниже второй. Теорема. Любой многочлен степени n вида P_n(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ представляется произведением постоянного множителя при старшей степени a_n и n линейных множителей (x-x₁), i=1, 2, …, n, то есть P_n(x)=a_n(x-x_n)(x-x_n-1)…(x-x₁) причемX_i, i=1, 2, …, n являются корнями многочлена. Эта теорема сформулирована для комплексных корней X_i, i=1, 2, …, n и комплексных коэффициентов a_k, k=0, 1, 2, …, n. Она является основой для разложения любого многочлена на множители. Если коэффициенты a_k, k=0, 1, 2, …, n – действительные числа, то комплексные корни многочлена ОБЯЗАТЕЛЬНО будут встречаться комплексно сопряженными парами. Замечание. Среди корней многочлена могут быть повторяющиеся. Доказательство теоремы проводится с использованием основной теоремы алгебры и следствия из теоремы Безу. Разложение на множители квадратного трехчлена. Квадратный трехчлен ax²+bx+c раскладывается на два линейных множителя: ax²+bx+c=a(x-x₁)(x-x₂), где х_{1 и} х₂ являются корнями (комплексными или действительными).Таким образом, разложение на множители квадратного трехчлена сводится к решению квадратного уравнения. Способы разложения на множители многочлена степени выше второй. В общем случае эта задача предполагает творческий подход, так как не существует универсального метода ее решения. Но все же попробуем дать несколько наводок. В подавляющем числе случаев, разложение многочлена на множители основано на следствии из теоремы Безу, то есть находится или подбирается корень и понижается степень многочлена на единицу делением на. У полученного многочлена ищется корень и процесс повторяется до полного разложения. Если же корень найти не удается, то используются специфические способы разложения: от группировки, до ввода дополнительных взаимоисключающих слагаемых.