
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения Фредгольма 2-ого рода с симметричным ядром
Ядро 1. Симметричное ядро, отличное от тождественного нуля, имеет, по крайней мере, одно характеристическое число. 2. Характеристические числа симметричного ядра действительны, а собственные функции, соответствующие различным характеристическим числам, ортогональны. На практике часто встречается случай, когда интегральное уравнение с симметричным ядром является решением некоторой самосопряженной однородной краевой задачи для обыкновенного дифференциального уравнения. В таких случаях нахождение характеристических чисел и собственных функций ядра сводится к решению указанной краевой задачи. Если задано неоднородное интегральное уравнение
с симметричным ядром
то его решение в общем случае может быть найдено следующим образом. Пусть
- последовательность характеристических чисел ядра
- соответствующая ортонормированная последовательность собственных функций. При этом в последовательности (46) каждое характеристическое число выписывается столько раз, каков его ранг, т.е. число линейно независимых функций, соответствующих этому характеристическому числу. Если параметр l в уравнении (45) не совпадает ни с одним характеристическим числом
где
Если же параметр l совпадает с одним из характеристических чисел, имеющим ранг r, т.е.
В этом случае уравнение имеет бесконечное множество решений, имеющих вид
где
10. Функциональные пространства Множество функций
Пусть Отображение Вариация функционала. Для любой Рассмотрим приращение функционала в произвольной внутренней «точке»
Если в приращении функционала можно выделить линейную часть по отношению к вариации
где
Рассмотрим однопараметрическое семейство функций
где
Первую вариацию также называют дифференциалом Гато (Гатó Рене Эжен – французский математик). Заметим, что из дифференцируемости по Фреше функционала I следует существование его первой вариации, которая в этом случае совпадает с дифференциалом, то есть
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 454; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.220.120 (0.008 с.) |
 называется симметричным, если оно удовлетворяет условию
называется симметричным, если оно удовлетворяет условию  для всех
для всех  . Для симметричных ядер, удовлетворяющих условию
. Для симметричных ядер, удовлетворяющих условию  , дополнительно к основным теоремам Фредгольма справедливы следующие утверждения:
, дополнительно к основным теоремам Фредгольма справедливы следующие утверждения: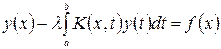 (45)
(45) (46)
(46)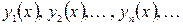 (47)
(47)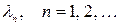 , то решение этого уравнения (существующее и единственное в силу 3-ей теоремы Фредгольма для любой правой части
, то решение этого уравнения (существующее и единственное в силу 3-ей теоремы Фредгольма для любой правой части  ) дается формулой
) дается формулой , (48)
, (48)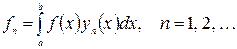 (49)
(49) для некоторого m, то решение существует в том и только в том случае, когда функция
для некоторого m, то решение существует в том и только в том случае, когда функция  . (50)
. (50) , (51)
, (51) - произвольные постоянные.
- произвольные постоянные. . Функционалы.
. Функционалы. и имеющих на этом отрезке непрерывные производные порядка k, образуют линейное пространство
и имеющих на этом отрезке непрерывные производные порядка k, образуют линейное пространство  . Например: пространство непрерывных функций
. Например: пространство непрерывных функций  ; пространство функций, имеющих непрерывную первую производную
; пространство функций, имеющих непрерывную первую производную  и так далее. Элементы этого пространства часто обозначают
и так далее. Элементы этого пространства часто обозначают  или просто
или просто  . Здесь точка в круглых скобках указывает на наличие аргумента, но его несущественную роль в обозначении элемента. Если в этих пространствах определить следующие нормы:
. Здесь точка в круглых скобках указывает на наличие аргумента, но его несущественную роль в обозначении элемента. Если в этих пространствах определить следующие нормы: - норма в
- норма в 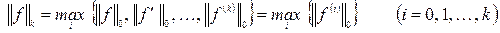
 - норма в
- норма в 
 .
. – некоторая функция. Множество функций
– некоторая функция. Множество функций  , для которых
, для которых  называют d – окрестностью функции
называют d – окрестностью функции  . Так как имеет место последовательное включение пространств
. Так как имеет место последовательное включение пространств  , в пространстве
, в пространстве  . В этом случае d – окрестность будет содержать функции более широкого класса; принято d – окрестность по норме
. В этом случае d – окрестность будет содержать функции более широкого класса; принято d – окрестность по норме  называть сильной d – окрестностью, а по норме
называть сильной d – окрестностью, а по норме  – слабой d – окрестностью. Согласно определению, слабая d – окрестность всегда содержится в сильной d – окрестности. Заметим, что пространство
– слабой d – окрестностью. Согласно определению, слабая d – окрестность всегда содержится в сильной d – окрестности. Заметим, что пространство  перестает быть банаховым. Это следует, например, из того факта, что не всякая непрерывная функция, являющаяся предельной для последовательности дифференцируемых функций, будет обязательно дифференцируемой.
перестает быть банаховым. Это следует, например, из того факта, что не всякая непрерывная функция, являющаяся предельной для последовательности дифференцируемых функций, будет обязательно дифференцируемой. множества
множества  на множество действительных чисел R называют функционалом и обозначают
на множество действительных чисел R называют функционалом и обозначают  ; множество D называют множеством допустимых функций для функционала I. Функционал
; множество D называют множеством допустимых функций для функционала I. Функционал 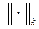 в «точке»
в «точке»  , если для любого
, если для любого  можно указать
можно указать 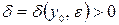 , такое что, как только
, такое что, как только  , то
, то 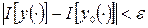 .
. называют вариацией функции
называют вариацией функции 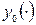 ; здесь
; здесь  . Таким образом, вариация функции сама является функцией из того же пространства, то есть
. Таким образом, вариация функции сама является функцией из того же пространства, то есть 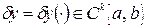 . Будем говорить, что «точка»
. Будем говорить, что «точка»  является внутренней для множества D, если она входит в него вместе с некоторой своей d – окрестностью.
является внутренней для множества D, если она входит в него вместе с некоторой своей d – окрестностью. .
. , то есть представить
, то есть представить ,
, – линейный функционал относительно
– линейный функционал относительно  – величина, имеющая более высокий порядок малости, чем
– величина, имеющая более высокий порядок малости, чем  , то линейная часть
, то линейная часть  ,
, – параметр,
– параметр, 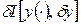 функционала I в «точке»
функционала I в «точке» 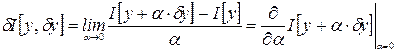 .
.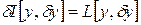 . Однако существование первой вариации функционала I еще не означает его дифференцируемости в соответствующей «точке»
. Однако существование первой вариации функционала I еще не означает его дифференцируемости в соответствующей «точке» 


