
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Линейное n – мерное векторное пространство. Линейная зависимость и независимость векторов. Ранг матрицы и системы векторов
Множество n-мерных векторов, в котором введены операции сложения и умножения на число, называется +—n-мерным векторным пространством (R(n))
Упорядоченная система из n действительных чисел +—n-мерным вектором
Коэффициенты при неизвестных всякого линейного уравнения с n неизвестными образуют +—n-мерный вектор
Суммой векторов +— Произведением вектора +— Скалярным произведением двух векторов +— Длиной вектора +— Вектор +— Система векторов +—хотя бы один из векторов системы является линейной комбинацией остальных Система векторов +— Если соотношение +—линейно независимой
Если некоторая подсистема +—линейно зависима
Всякая система векторов, содержащая два равных вектора, является +—линейно зависимой
Если система векторов линейно независима, то всякая ее подсистема +—линейно независима
Всякая система векторов, содержащая два пропорциональных вектора, является +—линейно зависимой
Если такая ее линейно независимая подсистема векторов, к которой нельзя присоединить ни одного вектора системы, не нарушив линейной независимости, то эта подсистема называется +—максимальной линейно независимой
Всякая система векторов, содержащая нулевой вектор является +—линейно зависимой
Число векторов, входящих в любую максимальную линейно независимую подсистему векторов, называется +—рангом системы
Максимальное число линейно независимых векторов системы +—из компонент векторов этой системы
Рангом системы векторов называется число векторов, входящих в любую
+—максимальную линейно независимую подсистему
Максимальное число линейно независимых строк матрицы равно +—максимальному числу линейно независимых столбцов матрицы
Любая совокупность n+1 векторов n–мерного векторного пространства +—линейно зависима
Максимальное число линейно независимых строк матрицы +—рангу этой матрицы
Базисом n–мерного векторного пространства называется любая совокупность +—n линейно независимых векторов этого же пространства
Любой вектор n–мерного векторного пространства можно представить как +—линейную комбинацию векторов базиса Система +—единичных векторов n–мерного векторного пространства
+—длиной вектора
Числа +—компонентами вектора
Любой вектор n–мерного пространства можно представить как линейную комбинацию векторов базиса +—единственным образом
Рангом матрицы A называется число r такое, что у матрицы существует +—хотя бы один отличный от нуля минор r–го порядка и равны нулю все миноры более высокого порядка(³r+1)
Если r-ранг матрицы А, то отличный от нуля минор r–го порядка называется +—базисным минором матрицы
Какое число линейно независимых векторов системы +—максимальное
Максимальное число линейно независимых столбцов матрицы +—рангу этой матрицы
Система векторов называется линейно независимой, если соотношение +— Число векторов, входящих в любую максимальную линейно независимую подсистем векторов, называется +—рангом системы
Указать совокупность векторов n – мерного векторного пространства, которая заведомо является линейно зависимой +—совокупность n+1 векторов
Для линейной независимости системы из n n – мерных векторов необходимо и достаточно, чтобы определитель, составленный из компонент векторов этой системы +—был отличен от 0
Система из пяти 4 – х мерных векторов
+—линейно зависима
Если Система векторов Компоненты вектора Векторы +— Векторы +—линейно зависимую систему Система векторов +—образует базис
Базисом +—любая группа из
Ранг матрицы равен числу ее +—линейно независимых строк
Рангом системы векторов называется число +—векторов в ее любом базисе
Ранг матрицы не изменится, если +—поменять местами два ее столбца
Если все миноры +—равны 0
Система линейных уравнений совместна тогда и только тогда, когда матрица, составленная из коэффициентов при неизвестных этих уравнений +—имеет ранг, равный рангу расширенной матрицы
Прибавление к одной строке матрицы другой строки, умноженной на некоторое число +—не меняет ранга матрицы
Умножение строки матрицы на некоторое число +—не меняет ранга матрицы
Тема 5. Неотрицательные решения систем линейных уравнений. Симплексные преобразования Опорными решениями называются +—неотрицательные базисные решения
Если в какой-либо строке таблицы Гаусса свободный член положителен, а все остальные элементы строки отрицательны или равны 0, то +—система не имеет неотрицательных решений
Опорные решения +—неотрицательны
Неотрицательные решения системы линейных уравнений находятся с помощью +—симплексных преобразований
При симплексных преобразованиях свободные члены уравнений должны быть +—неотрицательными
При симплексных преобразованиях за разрешающий столбец выбирается такой, в котором +—есть хотя бы одно положительное число
При симплексных преобразованиях элементы таблицы вычисляются по формулам +—Жордана-Гаусса
При симплексных преобразованиях расчет таблиц продолжается до тех пор, пока +—система не будет приведена к единичному базису
Переход от одного опорного решения к другому осуществляется с помощью +—симплексных преобразований
Количество опорных решений +—меньше или равно количеству базисных решений
При симплексных преобразованиях разрешающий элемент расположен на пересечении +—разрешающей строки и разрешающего столбца
Если правые части уравнений неотрицательны, то после симплексных преобразований они +—останутся неотрицательными
При симплексных преобразованиях число строк таблицы равно +—рангу системы
С помощью симплексных преобразований находятся +—опорные решения системы уравнений
Опорное решение – это +—базисное неотрицательное решение
Разрешающий элемент в симплексных преобразованиях +—положительный
При получении решения системы уравнений с помощью симплексных преобразований количество итерации равно +—количеству базисных переменных
Если при симплексных преобразованиях разрешающий элемент находится в строке с номером +— Если при симплексных преобразованиях разрешающий элемент находится в строке с номером
+— Решения систем линейных уравнений, которые принимают неотрицательные значения называются +—допустимыми
Совокупность всевозможных допустимых решений системы линейных уравнений называется +—областью допустимых решений
Последовательное применение симплексных преобразований позволяют определить все +—опорные решения системы
Указать среди базисных решений опорное +— Указать вариант, в котором свободные члены системы уравнений могут являться результатом симплексных преобразований, если до них они были неотрицательными +—(4, 5, 7, 3) Какое количество опорных решений не может соответствовать перечисленным ниже числам, если число базисных решений равно десяти +—11
Если все свободные члены системы неотрицательны, то после каких преобразований они останутся неотрицательными +—симплексных
Решения систем линейных уравнений называются допустимыми, если они принимают +—неотрицательные значения
Если система уравнений приведена к единичному базису и при этом ее свободные члены неотрицательны, то соответствующее системе решение является +—опорным
При симплексных преобразованиях в качестве разрешающего уравнения выбирается то уравнение, для которого отношение свободного члена к положительному элементу разрешающего столбца +—наименьшее
Система уравнений приведена к единичному базису. Ее решение является опорным, если свободные члены +—неотрицательные
Указать вариант, в котором свободные члены систем уравнений не могут являться результатом симплексных преобразований, если до них они были неотрицательными +—(2, -5, 6, -4)
При каком преобразовании разрешающий столбец выбирается так, чтобы он имел хотя бы один положительный элемент? +—при симплексном
В качестве какого уравнения выбирается уравнение системы, для которого отношение свободного члена к положительному элементу разрешающего столбца наименьшее +—разрешающего
Если система уравнений приведена к единичному базису и при этом хотя бы один из ее свободных членов отрицательный, то соответствующее системе решение не является +—опорным
Указать среди базисных решение, которое не является опорным +—
Переход от одного опорного решения к другому называется +—однократным замещением
При симплексных преобразованиях разрешающая строка отыскивается по правилу +— Если в i – м уравнении системы линейных уравнений все +—неотрицательных решений
Симплексные преобразования применяются для отыскании неотрицательных +—решений системы уравнений
Если в i – м уравнении системы линейных уравнений свободный член +—обе части i – ого уравнения надо умножить на (-1) и продолжить поиск опорных решений
Если при симплексных преобразованиях разрешающим элементом является Если разрешающим элементом в преобразованиях однократного замещения является В системе линейных уравнений
В системе линейных уравнений В системе линейных уравнений
В системе линейных уравнений
В системе линейных уравнений В системе линейных уравнений
Если в системе линейных уравнений с неотрицательными свободными членами после применения симплексного преобразования некоторые свободные члены стали отрицательными, то +—симплексное преобразование применено неверно В системе линейных уравнений
|
||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 2370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.55.14 (0.117 с.) |
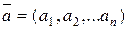 называется
называется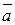 и
и  называется вектор
называется вектор



 , если существуют такие числа,
, если существуют такие числа, 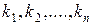 , при которых выполняется соотношение
, при которых выполняется соотношение
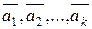 (k
(k  2) называется линейно зависимой, если
2) называется линейно зависимой, если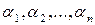 , не все равные нулю, при которых имеет место равенство
, не все равные нулю, при которых имеет место равенство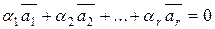
 возможно лишь в случае, когда
возможно лишь в случае, когда  , то система векторов называется
, то система векторов называется (r £ k) системы векторов
(r £ k) системы векторов  линейно зависима, то вся система
линейно зависима, то вся система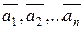 – линейно зависимая система векторов, а
– линейно зависимая система векторов, а 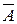 , составленной
, составленной называется системой
называется системой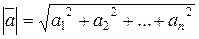 называется
называется , определяющие вектор
, определяющие вектор  справедливо лишь в случае, когда
справедливо лишь в случае, когда ,
, 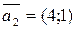 , то произведение
, то произведение  равно +—5
равно +—5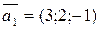 ,
,  ,
,  +—образует базис
+—образует базис в базисе
в базисе  ,
,  , где
, где  ,
, 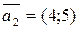 , равны +—(3;-1)
, равны +—(3;-1)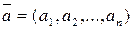 и
и  равны между собой, если
равны между собой, если
 образуют
образуют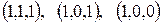
 - мерного пространства является
- мерного пространства является - го порядка матрицы
- го порядка матрицы  равны 0, то все ее миноры
равны 0, то все ее миноры  порядка
порядка
 и в столбце с номером k, то новые значения правых частей уравнения подсчитываются по формуле
и в столбце с номером k, то новые значения правых частей уравнения подсчитываются по формуле
 вычисляется по формуле
вычисляется по формуле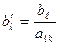

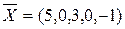

 ,
,  , то система не имеет
, то система не имеет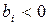 , то
, то , то новые элементы таблицы Гаусса
, то новые элементы таблицы Гаусса  определяются по правилу +—
определяются по правилу +— 
 в таблице Гаусса определяются по формуле +—
в таблице Гаусса определяются по формуле +— 
 опорное решение имеет вид +—(0,5,0,2)
опорное решение имеет вид +—(0,5,0,2) известно опорное решение
известно опорное решение 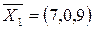 . Опорное решение
. Опорное решение  равно +—(4,3,0)
равно +—(4,3,0) опорное решение имеет вид +—(0,0,2,3)
опорное решение имеет вид +—(0,0,2,3) опорное решение имеет вид +—(0,5,0,3)
опорное решение имеет вид +—(0,5,0,3) известно опорное решение
известно опорное решение  . Опорное решение
. Опорное решение  известно опорное решение
известно опорное решение  . Опорное решение
. Опорное решение  известно опорное решение
известно опорное решение  и нужно найти второе опорное решение
и нужно найти второе опорное решение  равно +—(15,10,5)
равно +—(15,10,5)


