Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механический смысл второй производной ⇐ ПредыдущаяСтр 9 из 9
Пусть материальная точка движется прямолинейно по закону s=s(t), где s – путь, проходимый точкой за время t. Тогда скорость vэтого движения есть v= s'(t) = v(t), т.е. тоже некоторая функция времени. В момент времени t скорость имеет значение v=v(t). Рассмотрим другой момент времени t+Δt. Ему соответствует значение скорости v1 = v(t+Δt). Следовательно, приращению времени Δt соответствует приращение скорости Δv= v1 – v = v(t + Δt) – v(t). Отношение называется средним ускорением за промежуток времени Δt. Ускорением в данный момент времени t называется предел среднего ускорения при Δt→0:
. Таким образом, ускорение прямолинейного движения точки есть производная скорости по времени. Но как мы уже видели, скорость есть производная пути s по времени t: v = s'. Учитывая это, имеем: a = v'(t) = (s')' = s''(t), т.е. ускорение прямолинейного движения точки равно 2-й производной пути по времени a = S''(t). 43. Дифференциалы. Геометрический смысл дифференциала. Свойства дифференциала. Дифференциалы Для функций Дифференциал функции
где Таким образом Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция
Для отображений Дифференциалом отображения
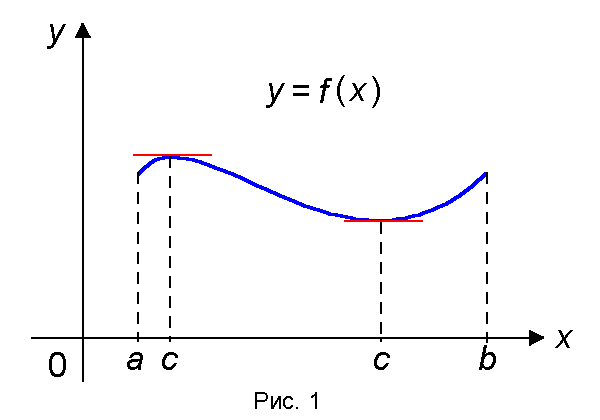
Геометрический смысл дифференциала Дифференциал функции f (x) в точке x 0 равен приращению, которое получает ордината касательной к кривой y = f (x) с абсциссой в точке x 0 при переходе из точки касания в точку с абсциссой x 0+Δ x.
Свойства дифференциала Дифференциал функции обладает свойствами, аналогичными свойствам производной. 1. Дифференциал постоянной равен нулю: 2. Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых: d(u+v)=du + dv Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны d(u+c) = du (c= const). 3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:
d(uv) = udv + vdu. Следствие. Постоянный множитель можно выносить за знак дифференциала d(cu) = cdu (с = const). 4. Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой
5. Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной. 44. Основные теоремы дифференциального исчисления (теорема Ферма, теорема Ролля, теорема Лагранжа). Теорема Ферма Теорема утверждает, что:
Теорема Ролля (Теорема Ролля) Пусть функция f (x)
Тогда существует точка c О (a, b) такая, что f '(c) = 0. Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 118. Геометрическая интерпретация теоремы Ролля Из теоремы Ролля следует, что существует точка с О (a, b), в которой касательная к графику функции f (x) параллельна оси О X (рис. 1).
Теорема Лагранжа (Теорема Лагранжа) Пусть функция f (x)
Тогда существует точка с О (a, b) такая, что
Формула (1) называется формулой Лагранжа, или формулой конечных приращений Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 119.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 599; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.13.173 (0.006 с.) |
 в точке
в точке  может быть определён как линейная функция
может быть определён как линейная функция
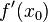 обозначает производную
обозначает производную 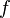 в точке
в точке  .
. есть функция двух аргументов
есть функция двух аргументов  .
. линейно зависящая от
линейно зависящая от  и для которой верно следующее соотношение
и для которой верно следующее соотношение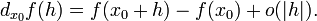
 в точке
в точке  называют линейны оператор
называют линейны оператор  такой, что выполняется условие
такой, что выполняется условие
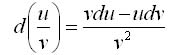
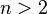 уравнение
уравнение
 не имеет натуральных решений
не имеет натуральных решений  ,
,  и
и  .
.