
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители n-ного порядка.
Определитель существует только для квадратной матрицы. Определитель матрицы – разность произведения элементов. Определитель матрицы = Детерминант матрицы Определитель квадратной матрицы – число, которое вычисляется по следующему правилу:
Пример:
Определитель второго порядка.
Определитель третьего порядка. Правило треугольника или Сюрриса.
Минор. Минором Алгебраическое дополнение Алгебраическим дополнением Теорема о понижении порядка определителя Теорема утверждает, что любой определитель равен сумме по парных произведений всех элементов какой либо строки (столбца) на алгебраические дополнения. Свойства определителей. 1. При транспонировании матрицы её определитель не меняется. 2. При перестановке двух строк определителя, он меняет свой знак, но по абсолютной величине не меняется. 3. При умножении определителя на число, достаточно умножить любую строку на это число. 4. Если определитель содержит нулевую строку, то он равен нулю. 5. Свойство упрощения определителя. Определитель не изменяется, если к элементам любой его строки прибавить элементы любой другой его строки, предварительно умножив их на одно и тоже любое число. 6. Сумма определителей, отличающихся одной строкой, равна определителю с теми же элементами, у которого вместо различных строк стоит строка из суммы элементов различных строк. 7. Если определитель имеет две пропорциональные строки, то он равен нулю. 8. Сумма попарных произведений элементов кокой либо строки и алгебраических дополнений соответствующих элементов другой строки равна нулю. 9. Определитель произведения двух квадратных матриц равен произведению их определителей. 10.Определитель треугольной матрицы равен произведению своих диагональных элементов. БИЛЕТ №2. Решение системы линейных алгебраических уравнений методом Жордана Гаусса.
Алгоритм:
1. В каждом уравнении выделить по одной базисной переменной (со знаком) 2. Выразить базисные переменные через остальные (свободные). 3. Выписать общее решение.
Базисная переменная – переменная, которая присутствует только в одном уравнении.
Метод Ж.Гаусса = Метод последовательного исключения
Обычно имеется общее и частное решение.
Если в каждом уравнении нет по базисной переменной, то следует сделать элементарные преобразования.
«КОНКУРС КРАСОТЫ» 1) КОНКУРС МЕЖДУ СТОЛБЦАМИ Складываем столбцами и выбираем меньшую переменную (без знаков) 2) КОНКУРС МЕЖДУ СТРОЧКАМИ Складываем строчками и выбираем меньшую переменную (без знаков)
Метод последовательного исключения неизвестных заключается в решении системы алгебраических уравнений с одновременным исследованием её на совместность. Метод реализуется в два этапа: Прямой ход метода. Прямой ход метода Гаусса заключается в преобразовании расширенной матрицы коэффициентов системы к ступенчатому виду с помощью элементарных преобразований, то есть как при нахождении ранга матрицы и базисного минора, но только со строками матрицы. При этом само преобразование к ступенчатому виду с помощью нескольких шагов, на каждом из которых исключается одна переменная, то есть обнуляется нижний элемент одного из столбцов. В результате выполнения нескольких шагов матрица оказывается приведённой к ступенчатому виду. На этом этапе можно определить ранг матрицы и системы. Если ранг расширенной матрицы равен рангу матрицы коэффициентов, то система считается совместной, в противном случае система не совместна. Если количество уравнений равно количеству неизвестных, то система имеет единственное решение, если ранг системы меньше числа неизвестных, то количество решений бесконечно. Обратный ход метода. Если решение единственно: БИЛЕТ №3.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 755; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.239.148 (0.006 с.) |
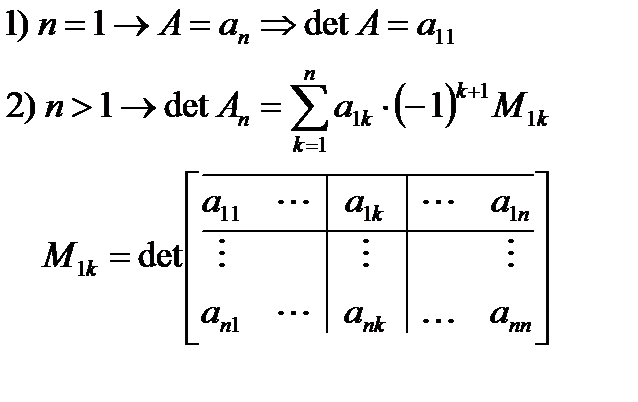
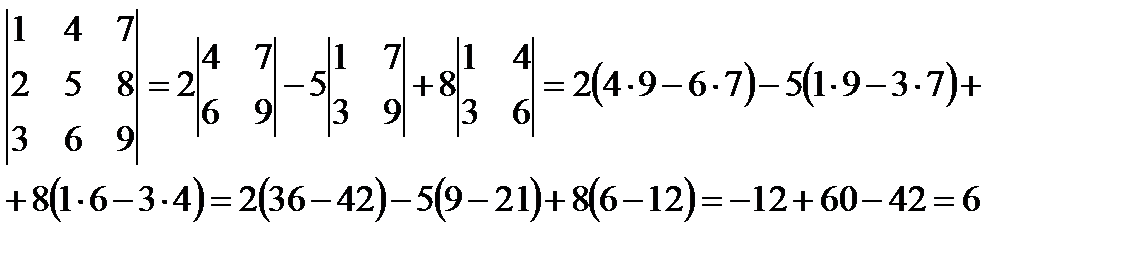
 (X перемножаем)
(X перемножаем) квадратной матрицы п -ного порядка называется определитель п- 1 -ого порядка, полученный из определителя матрицы А вычёркиванием i-той строки и j-того столбца.
квадратной матрицы п -ного порядка называется определитель п- 1 -ого порядка, полученный из определителя матрицы А вычёркиванием i-той строки и j-того столбца. называется минор этого элемента, взятый с определённым знаком, который определяется по формуле:
называется минор этого элемента, взятый с определённым знаком, который определяется по формуле: 




