
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція №1 Похідна функції однієї змінної. Властивості.Стр 1 из 7Следующая ⇒
Лекційно-практичний курс З математичного аналізу. Частина 2. Диференціальне Числення. Содержание Передмова. 3 Лекція №1 Похідна функції однієї змінної. Властивості. 4 Практичне заняття №1 Тема: Похідна. Диференційованість функції. 7 Практичне заняття №2 Тема: Властивості функцій диференційованих на відрізку. 9 Практичне заняття №3 Тема: Похідні та диференціали вищих порядків. Формула Тейлора. 11 Практичне заняття №4 Тема: Формула Тейлора. Обчислення границь за допомогою формули Тейлора. 13 Лекція №2 Дослідження на монотонність та екстремуми. Випуклі функції. Правило Лопіталя. 15 Практичне заняття №5 Тема: Правило Лопіталя. Використання похідної для розв’язання рівнянь, нерівностей, доведення нерівностей. 19 Практичне заняття №6 Тема: Використання похідної для розв’язання рівнянь, доведення тотожностей, розв’язання задач на мінімаксимум. 21 Практичне заняття №7 Тема: Дослідження функцій. 23 Диференціальне числення відображень. 25 Лекція №3 Лінійний нормований простір з скалярним добутком. Лінійні оператори. 25 Практичне заняття №8 Тема: Лінійний нормований простір зі скалярним добутком. Лінійні оператори. 30 Лекція №4 Похідна у напрямку. Частинні похідні. Повна похідна. 32 Практичне заняття №9 Тема: Частинні похідні. Похідна у напрямку. Повна похідна. 36 Лекція №5 Геометрична інтерпретація похідної відображення. Градієнт. 38 Практичне заняття №10 Тема: Геометричний зміст похідної функції. Механічний зміст похідної. 41 Лекція №6 Диференціал. Загальні закони диференціювання. 44 Практичне заняття №11 Тема: Диференціал функції. Загальні закони диференціювання. 46 Лекція №7 Формула скінчених приростів. 48 Лекція №8 Похідні вищих порядків. Формула Тейлора. 51 Практичне заняття №12 Тема: Похідна та диференціал вищого порядку. Формула Тейлора. 55 Лекція №9 Дослідження внутрішніх екстремумів. Дослідження екстремумів у випадку функцій двох змінних. 57 Практичне заняття №13 Тема: Дослідження екстремумів у випадку функцій кількох змінних. 60 Лекція №10 Теорема про неявну функцію.. 62 Лекція №11 Умовні екстремуми. 66 Практичне заняття №14 Тема: Умовні локальні екстремуми. 71 Література. 73 Передмова Пропонований посібник призначений для студентів фізико-математичного факультету спеціальності «Математика», а також може використовуватися студентами суміжних спеціальностей, у яких читається курс математичного аналізу.
Як і в першій частині, виклад матеріальну широко використовує елементи функціонального аналізу, що спрощує доведення властивостей. Факти, що стосуються більш конкретної ситуації формулюються у вигляді прикладів. Зазначимо, що ряд властивостей не доводяться, це стосується тих тверджень, які не важко знайти у загальнодоступній літературі, або довести самостійно у якості вправи. Як і в першій частині, протягом всього посібника лекції передуються з практичними заняттями. В кінці наводиться список літератури по теорії та практиці в сполученні з якими, ми сподіваємося, даний посібник допоможе засвоїти предмет більш глибше. Лекція №1 Похідна функції однієї змінної. Властивості. Нижче ми розглянемо означення та властивості похідної для функції однієї змінної. Однак, практично всі властивості приводяться без доведень (які можна легко знайти в книгах.1, 2.), з однієї сторони, оскільки їх не важко знайти та розібратися самостійно, а з іншої, оскільки подібні факти будуть доведенні нижче в більш загальній ситуації. Основні теореми диференціального числення для функції однієї змінної. Теореми Роля і Лагранжа. Нижче ми будемо говорити, що функція диференційована на множині Х, якщо вона диференційована в кожній точці множини Х. Теорема Роля. Нехай дійсна неперервна на відрізку Доведення. Якщо
Наступні дві теореми довести самостійно або знайти доведення у [1,2]. Теорема Лагранжа. (формула кінцевих приростів) Нехай функція
Теорема Коші. Нехай функції Доведення. Розглянемо функцію
Підставляючи в
Приклади. 1. 2. Зазначимо, що залишковий член у формулі Тейлора є
Дослідження монотонності. Наступна теорема легко доводиться за допомогою теореми Лагранжа та означення монотонності (див.[1,2] або доведіть самостійно). Теорема. Нехай функція Тоді: 1. 2. 3. 4. Опуклі функції. Означення. Функція
Означення. Функція
Перефразуємо означення.
або Отже, функція
( Доведення Необхідність. Нехай
Переходячи до границі в нерівності при
Достатність. 1. 2.
Опуклість вгору доводиться аналогічно. Наслідок. Для того, щоб функція Теорема. (нерівність Йенсена). Якщо функція Доведіть самостійно за допомогою математичної індукції. Приклад.
Покладемо Підставляючи, отримаємо нерівність Гельдера:
або
Нерівність Коші. Для будь-яких
Доведення.
Ця нерівність показує, що нерівність трикутника в звичайній метриці в Правило Лопіталя. Теорема. Нехай функції 1. 2. буде існувати Доведення. Доведемо випадок 1.
Функції
Для будь-якої послідовності
Отже, за Гейне Інший випадок розгляньте самостійно. Приклади. 1. 2. 3. Скалярний добуток у векторному просторі 4. Нехай 5. Нехай
6.
3. Простори неперервних лінійних операторів. Норма оператора Нехай Означення. Полілінійний оператор називається обмеженим на
Число Очевидно, що
Із властивостей лінійності
(
У випадку Приклади. 1.
2. Нехай у Х визначен скалярний добуток 3.
З іншого боку
тобто 4. 5. 6. Якщо Довести приклади 4, 5, 6 у якості вправ. Теорема. Для лінійного оператора 1. А – має скінчену норму; 2. А – обмежений оператор; 3. А – неперервний оператор; 4. А – неперервний в Доведення. Еквівалентність 1 і 2 очевидна. Доведемо еквівалентність 1, 2 і 3. Нехай А – обмежений, тобто Навпаки, нехай справедлива умова 3, тобто А – неперервне в Х. Покажемо, що А – обмежений. Нехай А необмежений, тобто існує Покажемо еквівалентність умов 3 і 4. Із умови 3 слідує умова 4. Доведемо, що з умови 4 слідує умова 3. Нехай А неперервний в 0. Якщо Зауваження. Аналогічне твердження справедливе коли А полілінійне відображення Теорема. Норма полілінійного оператора є нормою в лінійному просторі Доведення. Властивості норми легко довести з означення норми полінійного оператора. Покажемо, що L повний при умові, що Y повний. Нехай
Тоді
Перейдемо до границі при Легко довести слідуче твердження. Теорема. Якщо
Теорема. Між простором Доведення. Нехай,
. З означення оператора А випливає взаємно-однозначність відображення. Наслідок. Задачі Нехай Х – лінійний простір зі скалярним добутком. 1.1.Довести властивості скалярного добутку: 1. 2. 1.2. Довести нерівність Коші-Буняковського
1.3. Довести нерівність трикутника
для норми асоційованої зі скалярним добутком 1.4. Нехай Х скінчено вимірний лінійний простір зі скалярним добутком. Довести, що існує ортонормований базис у Х. Якщо
2.1. Нехай 2.2. Якщо 2.3. Якщо 2.4. Нехай Приклад.
Якщо Х і Y – скінчено вимірні з системами координат Нижче матрицю Якщо При Приклади. 1. 2. Матриця Якобі 2. Повна похідна Означення. Нехай Означення. Лінійна відносно h функція Теорема. Якщо відображення Доведення. Нехай
тобто f має похідну в точці х у будь-якому напрямку, і Покажемо, що похідна єдина. Якщо Неперервність f у точці х випливає з рівності Нехай Зауважимо, що в силу означення диференційованості випливає, що відображення, диференційоване в точці – неперервне у цій точці. Обернене невірне, наприклад, функція Зауваження. Умову диференційованості у точці Приклади. 1.
2. Якщо
3. Нехай
У координатній формі запису
Отже 4. Якщо
Якщо Але обернене твердження невірне. Наприклад:
Але в (0,0) функція не неперервна, значить і не диференційована. Задачі 1.1. 1.2. 1.3. 2.1. Знайти 2.2. Обчислити 2.3.
3.1. 3.2. 3.3. Приклади. 1. 2. 3. Визначимо зміст дотичного многовиду до графіка Е у точці Означення. Вектор 1.
2.
Якщо Дане означення можливо продемонструвати графічно наступним чином:
Означення. Множина дотичних векторів до Е у точці Теорема. Нехай Доведення. Спочатку проведемо допоміжні міркування. Нехай послідовності В силу неперервності
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 605; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.2.122 (0.188 с.) |
 функція
функція  диференційована на інтервалі
диференційована на інтервалі  . якщо при цьому
. якщо при цьому  , то існує
, то існує  , така, що
, така, що 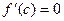 .
. , то теорема доведена. Розглянемо функцію
, то теорема доведена. Розглянемо функцію  . Тоді
. Тоді  задовольняє умови теореми і
задовольняє умови теореми і  і не є константою.
і не є константою.  на
на 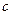 точка в якій
точка в якій  Аналогічно
Аналогічно  отже
отже 
 неперервна і диференційована на інтервалі
неперервна і диференційована на інтервалі 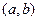 . Тоді
. Тоді  така, що
така, що  .
. і
і 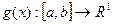 неперервні на
неперервні на 
 , то існує
, то існує  .
.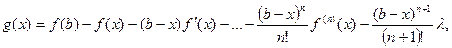 де
де 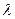 визначено так, щоб
визначено так, щоб  . Потрібно знайти
. Потрібно знайти  , то для визначення
, то для визначення  ,
,
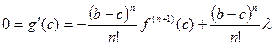 ,
,
 отримаємо необхідний результат.
отримаємо необхідний результат.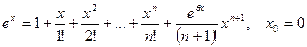 .
.
 , отже нижче формулу Тейлора будемо застосовувати у вигляді
, отже нижче формулу Тейлора будемо застосовувати у вигляді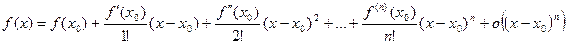 .
. і один раз диференційована на інтервалі
і один раз диференційована на інтервалі  не спадаюча на
не спадаюча на  не зростаюча на
не зростаюча на  строго зростає на
строго зростає на  строго спадає на
строго спадає на  називається опуклою вниз на
називається опуклою вниз на  і
і 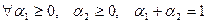 виконується нерівність
виконується нерівність .
. .
. ,
, 

 Тоді нерівність із першого означення набуде вигляду:
Тоді нерівність із першого означення набуде вигляду:



 .
.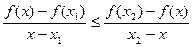 ,
,  ,
,  і
і  і
і  будемо мати
будемо мати

 . Отже, із зростання
. Отже, із зростання  ,
, означення опуклості вниз виконується.
означення опуклості вниз виконується. двічі диференційована на
двічі диференційована на  .
. і
і  , то
, то  .
. ,
,  опукла вниз, отже
опукла вниз, отже .
. .
.





 виконується.
виконується. диференційовані на
диференційовані на 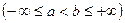 , причому
, причому  при
при  . Тоді в кожному з двох випадків
. Тоді в кожному з двох випадків при
при 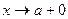 ,
, при
при 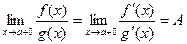 .
. ,
, 
 визначені на
визначені на  неперервні та диференційовані на
неперервні та диференційовані на  і задовольняють теорему Коші. Отже
і задовольняють теорему Коші. Отже 
 таке, що
таке, що або
або  ,
, 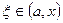
 існує послідовність
існує послідовність  і
і та
та  .
.
 – лінійний простір числових фінітних послідовностей
– лінійний простір числових фінітних послідовностей  ,
,  - лінійний оператор.
- лінійний оператор.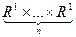 , А
, А  – n-лінійна функція
– n-лінійна функція 
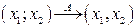 – білінійна функція.
– білінійна функція. – лінійне в Х. Якщо
– лінійне в Х. Якщо 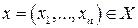 , то
, то 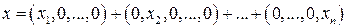 ,
,  ,
,  ,
,  – лінійне відображення і
– лінійне відображення і  – загальний вигляд,
– загальний вигляд,  .
. лінійне в Х, тоді
лінійне в Х, тоді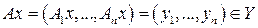 ,
,  – лінійні.
– лінійні. ,
, 
 – лінійне відображення. Якщо
– лінійне відображення. Якщо  , то
, то  – лінійне відображення, тобто
– лінійне відображення, тобто  – одержуємо знайомий числовий запис лінійного оператора
– одержуємо знайомий числовий запис лінійного оператора  .
.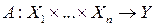 , де
, де  – нормовані простори.
– нормовані простори. , якщо
, якщо 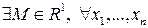 ,
, 
 .
. називається нормою А.
називається нормою А.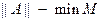 .
.
 – одиничний вектор з
– одиничний вектор з  ).
). .
. , якщо А обмежений, то одинична сфера переходить в еліпсоїд і норма співпадає з найбільшою піввіссю. З іншого боку, норма – верхня грань коефіцієнта розтягу векторів при даному відображенні.
, якщо А обмежений, то одинична сфера переходить в еліпсоїд і норма співпадає з найбільшою піввіссю. З іншого боку, норма – верхня грань коефіцієнта розтягу векторів при даному відображенні. – білінійне відображення, при
– білінійне відображення, при  маємо рівність
маємо рівність  і із нерівності Коші-Буняковського
і із нерівності Коші-Буняковського  .
. ,
, , тобто
, тобто  .
. ,
, .
. . У цьому випадку
. У цьому випадку  .
.
 .
. лінійний оператор, а
лінійний оператор, а 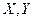 конечно вимірні нормовані простори, то А – має скінчену норму.
конечно вимірні нормовані простори, то А – має скінчену норму. , що діє з нормованого простору Х у нормований простір Y наступні умови рівносильні:
, що діє з нормованого простору Х у нормований простір Y наступні умови рівносильні: .
. . Нехай
. Нехай  (де
(де  - будь-яка точка з Х) в Х, тоді
- будь-яка точка з Х) в Х, тоді  , тобто А неперервний в
, тобто А неперервний в  , тобто у Х.
, тобто у Х. така, що
така, що 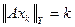 , і
, і  , тоді послідовність
, тоді послідовність 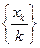 така, що
така, що  – це суперечить неперервності А, тобто припущення невірне.
– це суперечить неперервності А, тобто припущення невірне.
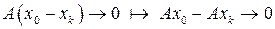 , тобто
, тобто  – А неперервний в
– А неперервний в  .
. ,
,  – множина неперервних полілінійних операторів.
– множина неперервних полілінійних операторів. . Якщо при цьому Y – повний, то L – повний нормований простір.
. Якщо при цьому Y – повний, то L – повний нормований простір. послідовність Коші, тобто
послідовність Коші, тобто  , що
, що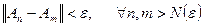 .
. послідовність Коші в Y, оскільки
послідовність Коші в Y, оскільки  , отже
, отже 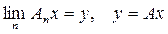 . Покажемо, що
. Покажемо, що  по нормі.
по нормі. ,
,  .
.
 тобто
тобто  , отже
, отже  .
. , то
, то 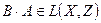 і
і .
.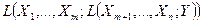 і
і  тобто
тобто . Покладемо
. Покладемо , тоді
, тоді 
 ізоморфний
ізоморфний 





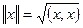 .
. ортонормований базис, то
ортонормований базис, то  .
. , а
, а  . Довести, що оператор
. Довести, що оператор 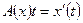 - лінійний оператор з
- лінійний оператор з  .
. , то загальний лінійний оператор
, то загальний лінійний оператор  з нормою
з нормою 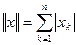 . Довести, що
. Довести, що 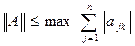 , де А – лінійний оператор з
, де А – лінійний оператор з  , а
, а  - відповідна матриця.
- відповідна матриця. (оператор добутку на функцію
(оператор добутку на функцію  )
)  - неперервна функція. Довести лінійність А та
- неперервна функція. Довести лінійність А та  .
. .
. і
і  .
.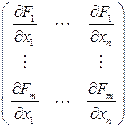 будемо називати матрицею Якобі f у точці х.
будемо називати матрицею Якобі f у точці х. , то визначник матриці називається визначником Якобі (Якобіан) і позначається
, то визначник матриці називається визначником Якобі (Якобіан) і позначається  .
. він спрощується до звичайної похідної.
він спрощується до звичайної похідної.
 .
.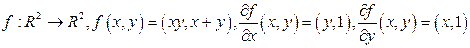
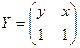 .
. називається диференційованим у точці
називається диференційованим у точці  , якщо існує таке лінійне неперервне відображення
, якщо існує таке лінійне неперервне відображення  що
що  , де
, де  при
при  , тобто
, тобто  .
. називається дотичним відображенням або похідною відображення
називається дотичним відображенням або похідною відображення  в точці х. Позначення:
в точці х. Позначення:  .
. , то його похідна єдина. У цьому випадку f неперервне в х. Крім того, у точці х відображення f має похідну вздовж будь-якого напрямку
, то його похідна єдина. У цьому випадку f неперервне в х. Крім того, у точці х відображення f має похідну вздовж будь-якого напрямку  , а відображення
, а відображення 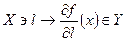 лінійне неперервне відображення
лінійне неперервне відображення  і
і  .
.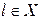 , покладаючи в означенні похідної
, покладаючи в означенні похідної  маємо
маємо  , або
, або 

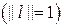 , при
, при  отримаємо, що
отримаємо, що  ,
, неперервне і лінійне по l.
неперервне і лінійне по l. і
і 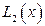 – похідні f, то
– похідні f, то  ,
,  , тобто
, тобто  .
. , тобто маємо
, тобто маємо  .
. диференційована в кожній точці
диференційована в кожній точці  , тобто диференційована на Х, то виникає функція
, тобто диференційована на Х, то виникає функція  , яку називають похідною від f або похідним відображенням. Значення
, яку називають похідною від f або похідним відображенням. Значення 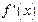 в точці
в точці  , яка є диференціалом або похідною функції f у даній конкретній точці
, яка є диференціалом або похідною функції f у даній конкретній точці 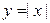 в точці х =0 неперервна, але не диференційована.
в точці х =0 неперервна, але не диференційована. можна записати так:
можна записати так: 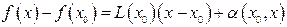 ,
,  при
при  . Зрозуміло, що означення насправді відноситься до відображень
. Зрозуміло, що означення насправді відноситься до відображень  будь-яких афінних просторів
будь-яких афінних просторів  , лінійні простори Х і Y яких нормовані.
, лінійні простори Х і Y яких нормовані.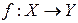 , Х – скінчено вимірна зі скалярним добутком,
, Х – скінчено вимірна зі скалярним добутком,  - ортонормований базис в Х, а
- ортонормований базис в Х, а  де
де 
 то
то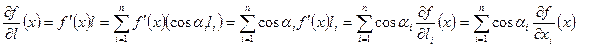
 , то для будь-якого напрямку
, то для будь-якого напрямку 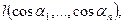
 Отже
Отже 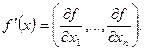
 , де
, де  - ортонормовані базиси у
- ортонормовані базиси у  і
і  відповідно.
відповідно.
 , маємо, для будь-якого
, маємо, для будь-якого  .
.
 (у координатній формі запису).
(у координатній формі запису).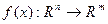 , то
, то  Отже, з приклада 3 маємо
Отже, з приклада 3 маємо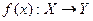 і існує
і існує  у деякій точці х, то існують
у деякій точці х, то існують  (х), тобто існує матриця Якобі у х.
(х), тобто існує матриця Якобі у х.

 Знайти
Знайти  .
. . Знайти
. Знайти  та матрицю Якобі.
та матрицю Якобі.
 . Знайти
. Знайти 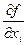 .
.
 .
.
 , де
, де 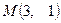 , а l – направлення від
, а l – направлення від  .
. . Обчислити
. Обчислити 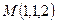 у направленні l, що утворює з осями координат кути 60º, 45º, 60º відповідно.
у направленні l, що утворює з осями координат кути 60º, 45º, 60º відповідно.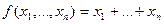 . Знайти
. Знайти 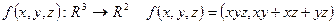 . Знайти
. Знайти 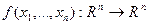
 Знайти
Знайти 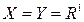 , Е – крива в
, Е – крива в 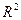 .
. , Е – поверхня в
, Е – поверхня в  .
. Е – крива в
Е – крива в  , що описується рівняннями
, що описується рівняннями  .
. .
. називається дотичним у точці
називається дотичним у точці  до графіка Е, якщо:
до графіка Е, якщо: , така, що
, така, що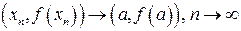 в
в  ,
,
 , для яких виконується граничне співвідношення
, для яких виконується граничне співвідношення 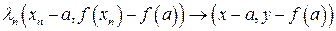 в
в  .
. – дотичний вектор до Е в
– дотичний вектор до Е в  , то
, то  також дотичний вектор до Е в
також дотичний вектор до Е в 
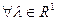 .
.
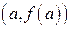 , що є підмножиною в
, що є підмножиною в  називається дотичним до многовида Е у точці
називається дотичним до многовида Е у точці  .
.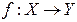 диференційована в
диференційована в  . Дотичний підпростір до
. Дотичний підпростір до  у точці
у точці  є підпростором у
є підпростором у  , що визначається рівнянням
, що визначається рівнянням  , тобто це множина
, тобто це множина  .
. і
і  ,
,  . За означенням похідної відображення маємо:
. За означенням похідної відображення маємо:  , при
, при  . Тоді
. Тоді  .
.
 ;
;


