
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дослідження намагнічування феромагнетиків
ЗА ДОПОМОГОЮ ОСЦИЛОГРАФА
ПРИЛАДИ: звуковий генератор; осцилограф; тороїдальний феромагнетик з двома обмотками; схема підключення. Феромагнетиками називають речовини, які мають велику магнітну проникність. У пара- та діамагнетиків магнітна проникність відрізняється від одиниці на величину порядку 10-5-10-4. У феромагнетиків проникність на багато більша за одиницю; у звичайної сталі вона становить декілька сотень, а у рекордних сплавів перевищує 106.
Рис 12.1 Криві гістерезису: а) незамкнутий цикл, б) замкнутий цикл. в) граничний цикл.
До феромагнетиків належать залізо, нікель, кобальт, гадоліній, їх численні сплави з іншими металами. Феромагнітними властивостями володіють деякі сплави елементів, які нарізно не є феромагнітні (наприклад, сплав міді та марганцю), та ряд неметалевих речовин (ферити). Магнітна індукція Якщо прикладати магнітне поле до розмагніченого зразка (рис.12.1 в), тоді його намагнічування зростатиме по кривій ОD′DЕ, яка виходить з початку координат. Цю криву називають основною кривою намагнічування. Індукція
де m0 - магнітна стала, m – магнітна проникність речовини. Крива намагнічування ОD′DЕ, яка зображує залежність В (Н), практично співпадає з залежністю І (Н), тому як другий член у виразі (12.1) – у звичайному діапазоні зміни полів - суттєво перевищує перший. У точці Е намагніченість І досягає насиченості, тому подальше незначне збільшення індукції відбувається, як правило, у зв’язку з ростом При невеликих
Намагнітимо зразок до насичення - до точки Е. При зменшенні напруженості магнітного поля Щоб привести до нуля магнітну індукцію Замкнута крива EDFGBABCDE, яка утворюється при циклічному перемагнічуванні зразка, називається кінцевою петлею гістерезису. Площа петлі гістерезису ∫ НdВ (у системі СІ) визначає роботу, яка виконується зовнішнім полем при перемагнічуванні одиниці об’єму зразка. Ця робота повністю переходить у теплоту, так що при перемагнічуванні зразок нагрівається. Якщо розмістити зразок у невеликому змінному магнітному полі, яке неспроможне довести його до стану насичення, тоді крива, яка характеризує змінну В у залежності від Форма кривих, які зображують як часткові цикли, так і кінцевий цикл, залежить від частоти. Їх форма визначається не тільки магнітними властивостями речовини, але й величиною струмів Фуко, котрі швидко зростають з частотою. Зі зростанням частоти криві гістерезису розширюються у відповідності із зростанням втрат енергії. «Динамічна петля» гістерезису (петля при w >) завжди ширша «статичної» (петлі, знятої при полі Н, яке повільно змінювалося).
Уточнимо поняття магнітної проникності феромагнетиків. Магнітною проникністю m називають або відношення В/Н, або похідну В по Н; у першому випадку говорять про повну, а у другому - про диференційну магнітну проникність речовини:
mповн = В m-0Н, mдиф = dВ m0 dН,
де m0 - магнітна постійна, яка дорівнює у системі СІ 4p×10-7 Гн/м., m0 = 1 у системі СГС. Як було зазначено вище, магнітна проникність феромагнетиків залежить від поля. Початковою магнітною проникністю називають величину m, яка вимірюється при невеликих Метою роботи є дослідження кривих гістерезису феромагнетиків за допомогою осцилографа. Цей спосіб не належить до числа точних, але відрізняється простотою, переконливістю, та наглядністю. Розглянемо феромагнітний зразок, який має форму тора. Нехай малий радіус тора r значно менший його середнього радіусу r. Позначимо через N 0 кількість витків обмотки, яка намагнічує зразок; через І0 - силу струму, який намагнічує. Нехай
звідки Н = N0I0/ 2 pr (12.2)
Магнітну індукцію зручно визначати за допомогою Е.Р.С., яка при зміні магнітного струму Ф виникає у котушці, що охоплює зразок:
ℰ = - dФ dt.
Нехай котушка охоплює зразок, і індукція В у зразку однорідна. У такому випадку: Ф = SNB, де N - кількість витків у вимірювальній котушці; S - площа витка. Підставляючи це значення у попередню формулу, після інтегрування знайдемо:
В = - I ∫ℰ dt / SN. (12.3)
Таким чином, для визначення В необхідно проінтегрувати сигнал, наведений змінним магнітним полем у вимірювальній котушці, намотаній на зразок.
Рис.12.2 Найпростіша інтегруюча схема.
Для інтегрування електричного сигналу застосовують різного роду інтегруючі схеми. Простіша з них складається із з’єднаних послідовно резистора та конденсатора (рис.. 12.2). Дана схема виконує своє призначення, якщо вихідний сигнал набагато менший вхідного:
Uвих << Uвх.
Насправді, коли виповнюється ця умова І» Uвх/R та
Uвих =
Ми бачимо, що вихідний сигнал RC - ланцюга дійсно пропорційний інтегралу від вхідного. Цей висновок тим ближче до істини, чим більше добуток RC, який носить назву “постійна часу” RC – ланцюга, перевищує характерний час процесу, наприклад його період. У феромагнітних речовинах є не парні (відповідальні за феромагнетизм) електрони, спіни яких у порівняно великих областях орієнтуються у одному напрямку. Кожна з таких областей, яка називається доменом, намагнічена до стану насиченості. В ненамагніченому (розмагніченому) феромагнетику вектори намагніченості доменів направлені хаотично. При дії зовнішнього магнітного поля відбувається переорієнтація векторів намагніченості всіх доменів. Вони виявляються спрямовані вздовж збуджуючого поля. Відбувається: по-перше, намагнічування феромагнетика; по-друге підсилення магнітного поля, оскільки за принципом суперпозиції до зовнішнього (збуджуючого) магнітного поля додається магнітне поле феромагнетика.
Схема експериментальної установки показана на рис. 12.3. Осцилограф в даній схемі використовується як характернограф, коли два сигнали, що перебувають у функціональній залежності, подаються одночасно на два входи осцилографа. Незалежна величина подається на вхід Х (в нашому випадку, це сигнал, пропорційний збуджуючому полю Н). Цей сигнал здійснює відхилення променя осцилографа по горизонталі. Залежна величина, тобто сигнал, пропорційний намагніченості зразка, подається на вхід Y і відхиляє промінь осцилографа по вертикалі. Сигнал звукового генератора подається на намагнічуючу обмотку N0 зразка, який досліджується. Вимірювальна обмотка Nu приєднана до інтегруючого RC- ланцюга. Через обмотку N0 пропускається змінний струм І0. Даний струм визначає величину магнітного поля Н в котушці N 0, яка намагнічує зразок:
Проте струм не можна подавати на вхід осцилографа, оскільки управління положенням променя в ньому здійснюється потенціалом (напругою). Ввімкнувши послідовно з котушкою N 0 опір R 0 отримаємо на ньому падіння напруги
Експериментальна установка
Сигнал Uс з інтегруючої ємності Сu пропорційний величині вектора В подається на вхід “У” осцилографа. Рисунок, що з’являється на екрані осцилографа у деякому масштабі (величини якого по осям X та У не дорівнюють одна одній), відтворює петлю гістерезису зразка, який досліджується. Щоб дати цій кривій кількісну міру, необхідно встановити масштаб зображення, тобто провести калібрування горизонтального та вертикального каналів осцилографа. Значення масштабних коефіцієнтів, які були встановлені при калібруванні, вказані на осцилографі. Калібрування вертикальної та горизонтальної осей осцилографа слід використовувати для побудови петель гістерезису в осях В та Н. Значення Н розраховуються за допомогою рівняння (12.5). Для перерахунку напруги UY = U вих, на вході осцилографа, в значення В слід скористатись рівнянням (12.4). Враховуючи те, що напруга на вході інтегруючого RC – ланцюжка визначається як: Uвх = - dФ / dt = - SNu / dt,
Рис.12.3 Схема експериментальної установки.
отримаємо напругу на виході інтегруючого кола U вих, що являється одночасно вхідною напругою осцилографа по входу Y, як
Uвих = UY= - (∫ SNudB / dt) / RCu = - SNuB / RCu. Звідки В = - UYRCu / SNu. (12.6)
У рівнянні (12.6) через Nu позначено кількість витків вимірювальної обмотки, S - площа поперечного перерізу осердя зразка. У експериментальній установці: N0 = 50; Nu = 200; 2 pr = l = 76,9мм; S = 43,8 мм2; R 0 = 100 Oм; R = 7,5 kOм; Cu = 0,47 мкФ.
Завдання
1. Зібрати робочу схему згідно рис. 12.3. 2. Увімкнути живлення та отримати на екрані осцилографа петлю гістерезису. З цього моменту та до закінчення роботи положення ручки підсилювача осцилографа не змінювати. 3. Змалювати на кальку петлю гістерезису яка спостерігається на екрані. Записати значення масштабних коефіцієнтів для визначення U0 і Uу. Обчислити Н і В. 4. Визначити масштабні коефіцієнти h, b. За допомогою рівнянь (12.5) та (12.6) побудувати петлю гістерезису у координатах В та Н. 5. Визначити значення коерцитивної сили та залишкової індукції. 6. Визначити значення повної магнітної проникності у точці насичення. 7. За допомогою координатної сітки визначити площу петлі гістерезису та визначити роботу, яка була витрачена на перемагнічування одиниці об’єму за один цикл. Для цього необхідно оцінити значення інтегралу:
А = ò ВdH = Snbh.
8. Оцінити помилки вимірювання всіх величин.
Контрольні запитання
1. Що таке статична петля гістерезису? 2. Які феромагнетики називаються магнітом’ягкими, а які магнітожосткими? 3. Від чого залежить форма петлі гістерезису? 4. Як зміниться індукція В всередині тороїда, який обтікає незмінний струм, при заповненні його: парамагнетиком; діамагнетиком? 5. Що називають магнітною проникністю феромагнетиків? У яких одиницях вона вимірюється? 6. Які особливості макро - та мікроструктури феромагнетиків?
Література
1. Сивухин Д.В. Общий курс физики. - М.: Наука, 1983, п. 74. 2. Калашников С.Г. Электричество. - М.: Наука, 1977, п. 110, 111, 118, 119. 3. Лабораторные занятия по физике. /Под ред. Гольдина Л.Л. - М.: Наука, 1983. Лабораторна робота № 13
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 686; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.115.120 (0.061 с.) |

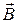 та напруженість магнітного поля
та напруженість магнітного поля  у феро –магнетиків не однозначно зв’язані один з одним: індукція В залежить не тільки від напруженості магнітного поля
у феро –магнетиків не однозначно зв’язані один з одним: індукція В залежить не тільки від напруженості магнітного поля  , (12.1)
, (12.1) - намагніченість - магнітний момент одиничного об’єму зразка;
- намагніченість - магнітний момент одиничного об’єму зразка;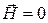 зразок має ненульову індукцію В r (залишкова індукція). Величина залишкової індукції значно залежить від складу та термообробки феромагнетику. У магнітожорстких зразків, з яких виготовляють постійні магніти, В r може мало відрізнятись від індукції насичення.
зразок має ненульову індукцію В r (залишкова індукція). Величина залишкової індукції значно залежить від складу та термообробки феромагнетику. У магнітожорстких зразків, з яких виготовляють постійні магніти, В r може мало відрізнятись від індукції насичення.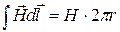 ,
,
 =
=  »
» 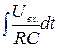 (12.4)
(12.4) . (12.5)
. (12.5) . Якщо напругу U 0 подати на вхід Х осцилографа, то променем осцилографа в горизонтальному напрямку буде керувати напруга U 0, пропорційна струму І 0 , якому в свою чергу пропорційна напруженість поля Н 0, тоді:
. Якщо напругу U 0 подати на вхід Х осцилографа, то променем осцилографа в горизонтальному напрямку буде керувати напруга U 0, пропорційна струму І 0 , якому в свою чергу пропорційна напруженість поля Н 0, тоді: .
.



