
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Випадкові події. Класифікація подій. Класичне означення поняття ”Ймовірність”. Відносна частота(частість). Статистичне означення поняття “ЙмовірністьСтр 1 из 4Следующая ⇒
Випадкові події. Класифікація подій. Класичне означення поняття ”Ймовірність”. Відносна частота(частість). Статистичне означення поняття “Ймовірність Випадковою подією, яка може настати (з’явитись) або не настати у даному випробуванні. Достовірною подією, яка обов’язково настає у даному випробуванні. U. Неможливою подією, яка не може настати у даному випробуванні. Неможливу подію позначатимемо V. Попарно несумісними подіями (несумісними у сукупності), якщо у даному випробуванні ніякі дві з них не можуть настати разом (поява однієї із подій виключає появу будь-якої іншої). У супротивному випадку події називають сумісними. Єдино можливими подіями, якщо у даному випробуванні обов’язково настане хоча б одна із цих подій. Події утворюють повну групу, якщо вони єдино можливі та попарно несумісні. Дві події Події називаються рівноможливими, якщо вони мають однакові шанси до появи у даному випробуванні. Простір елементарних подій – усі єдино можливі, рівноможливі та несумісні події, які неможливо поділити на більш прості події. Імовірність події A дорівнює: P(A)= m/n деn - число (кількість) подій у просторі елементарних подій, а m - число наслідків (із простору елементарних подій), які сприяють появі події A. Означення. Нехай проводиться n випробувань (які можна повторювати при незмінних умовах необмежено). Частотою m(A) називається кількість випробувань (із n), в яких з’явилась подія A. Частістю (відносною частотою або часткою) w(A)=m(A)/n називається відношення частоти появи події A до загальної кількості випробувань. Статистичною імовірністю події A називають число, що характеризує можливості появи події і яке дорівнює: P(A)=lim w(A).
Класичне означення ймовірності події. Властивості ймовірності. Теорема добутку ймовірностей та наслідки з неї. Імовірність події A дорівнює: P(A)= m/n деn - число (кількість) подій у просторі елементарних подій, а m - число наслідків (із простору елементарних подій), які сприяють появі події A. Властивості: 1. Для довільної події A: 2. Для достовірної події U: P(U)=1 3. Для неможливої події V: P(V)=0. Теорема (добутку імовірностей). Імовірність добутку двох подій A і B дорівнює добутку імовірності однієї з них на умовну імовірність іншої, при умові, що настала перша подія:
Наслідок 1 (формули визначення умовних імовірностей). Якщо імовірності подій відмінні від нуля, то
Зауважимо, що теорема добутку справедлива навіть у випадку нульових імовірностей подій Наслідок 2. Якщо подія A не залежить від події B, то і навпаки, подія B не залежить від події A, тобто вони взаємно незалежні. Наслідок 3. Із незалежності подій A і B випливає незалежність пар подій: Наслідок 4. Імовірність добутку двох незалежних подій дорівнює добутку їх імовірностей: P(AB)=P(A)*P(B) Довести теорему суми ймовірностей та 3 наслідки з неї. Теорема. Імовірність суми двох подій A і B дорівнює сумі імовірностей цих подій без імовірності їх добутку. Іншими словами, імовірність появи хоча б однієї із двох подій дорівнює сумі їх імовірностей без імовірності їх сумісної появи: P(A+B)=P(A)+P(B)-P(AB) Доведення:
= P (A) + P (B)-P(AB) Наслідок 1. Імовірність суми двох несумісних подій дорівнює сумі їх імовірностей: P(A+B)=P(A)+P(B). Наслідок 2. Сума імовірностей подій A1, А2,.....,Аn, що утворюють повну групу, дорівнює одиниці: P (A1)+P(A2)+….+P(An)=1 Доведення:
Наслідок 3. Для взаємно протилежних подій A і
Доведення випливає із попереднього наслідка 2. Наслідок4. Імовірність появи хоча б однієї із подій A1,A2,…..,An дорівнює: Зокрема, якщо події незалежні в сукупності, то:
Доведення: 4. Довести теореми (формула повної ймовірності та формули Байєса). Теорема. Нехай подія A може настати лише сумісно з хоча б однією із подій-гіпотез H1, H2….Hn, які утворюють повну групу. Тоді імовірність (повна імовірність) події A дорівнює: тобто сумі добутків ймовірностей гіпотез на умовні ймовірності події, при умові, що настала відповідна гіпотеза Доведення: Формули Байєса. Теорема. Нехай подія A може настати лише сумісно з хоча б однією із подій-гіпотез H1, H2….Hn, які утворюють повну групу. Якщо подія A настала, то умовні (уточнені) імовірності гіпотез дорівнюють:
де повна імовірність Доведення: Зазначимо, що виконуються усі умови теореми – формули повної ймовірності. Розглянемо одну із подій AHi і скористуємось теоремою добутку:
P(AHi)=P(A)Pa(Hi)=P(Hi)Phi(A). Звідси:
Незалежні повторні випробування – НВП. НВП як випробування, проведені за схемою “повернених куль”. Виведення формул для математичного сподівання, дисперсії та середнього квадратичного відхилення частоти та відносної частоти в схемі незалежних повторних випробувань. Означення. Якщо серію n випробувань проводити в однакових умовах і імовірність появи події A в кожному окремому випробуванні однакова та не залежить від появи або непояви події A в інших випробуваннях, то таку послідовність НПВ називають схемою Бернуллі. Прикладами НПВ є: кидки монети (подія A - випадіння цифри), діставання кулі за схемою «повернених куль» із урни з різнокольоровими кулями (подія A - діставання кулі певного кольору), контроль якості серії виготовлених автоматом деталей (подія A - бракована деталь) тощо. Теорема. Нехай проводиться n НПВ за схемою Бернуллі і ймовірність появи події A в кожному із випробувань p = P(A) незмінна (ймовірність непояви події A в кожному із випробувань
9.Формула Бернуллі. Біноміальний закон розподілу ймовірностей (закон Бернуллі). Найімовірніша частота (мода) настання події. Локальна теорема Лапласа. Формула Пуассона. Закон рідкісних подій (закон Пуассона).
Біноміальным законом розподілу ДВВ X називають ДВВ X = m – частоту появи події A у n НПВ, таблиця розподілу якої має наступний вигляд
M(m) = np; D(m) = npq; Найімовірнішою частотою m0 (або модою) появи події A у n НПВ називають частоту, для якої За означенням із системи умов
неважко дістати подвійну нерівність для визначення найімовірнішої частоти:
Теорема (локальна формула Муавра-Лапласа). Якщо у схемі Бернуллі із n НПВ імовірність появи події A дорівнює p (0 < p < 1), а кількість НПВ досить велика, то імовірність появи події A m разів у n НПВ наближено дорівнює (тим точніше, чим більше n):
Формула Пуассона:
Означення. При виконанні умов теореми Пуассона ВВ Х = m (яка приймає нескінченну злічену множину значень m = 0,1,2///, а відповідні імовірності знаходяться за формулою
Закон великих чисел. Центральна гранична теорема. Інтегральна теорема Муавра-Лапласа. Частинні випадки теореми Муавра-Лапласа. Нерівність Маркова. Нерівність Чебишева. Частинні випадки нерівності Чебишева. Теорема Бернуллі. Збіжність за ймовірністю. Теорема Чебишева. Закон великих чисел із уточненням Ляпунова. Центральна гранична теорема-якщо всі ВВ однаково розподілені, то закон розподілу їх суми при Інтегральна теорема Муавра-Лапласа. Для біноміально розподіленої ДВВ X=m - частоти появи події A з імовірністю p в серії із n НПВ справедлива наближена формула:
де Ф(t) - інтегральна функція Лапласа. Частинні випадки інтегральної теореми Муавра-Лапласа. Для частоти m та частості m/n появи події A з імовірністю p в серії із n НПВ справедливі наближені формули:
Якщо ВВ X приймає тільки невід’ємні значення і має фіксоване математичне сподівання M(X), то для довільного додатного числа a справедлива нерівність:
Теорема (нерівність Чебишова). Якщо довільна ВВ x має фіксовані математичне сподівання M(X) та дисперсію D(X), то для довільного додатного числа
ЧАСТИННІ ВИПАДКИ НЕРІВНОСТІ ЧЕБИШОВА.
а) для біноміально розподіленої ДВВ X = m - частоти появи події A з імовірністю p в серії із n НПВ:
б) для біноміально розподіленої ДВВ
Теорема Бернуллі Частість m/n появи події A в серії із n НПВ при
Послідовність називається збіжною за імовірністю до величини a (сталої або випадкової), якщо для довільного як завгодно малого числа
Теорема Ляпунова. Тоді закон розподілу суми
Статистичний розподіл ознаки. Статистична сукупність. Кількісні та якісні ознаки. Варіанта та її частоти або частки. Дискретні варіаційні ряди та їх полігони частот або часток ознаки. Інтегральні варіаційні ряди та їх гістограми щільності частот (часток) ознаки. Характеристики варіаційного ряду: варіаційний розмах, коефіцієнт варіації, середнє значення та дисперсія ознаки у даній статистичній сукупності. Нехай потрібно вивчити сукупність об’єктів відносно деякої якісної або кількісної ознаки (випадкової величини), які характеризують ці об’єкти. Кожен об’єкт, який спостерігають, має декілька ознак. Розглядаючи лише одну ознаку кожного об’єкта, ми припускаємо, що інші ознаки рівноправні, або що множина об’єктів однорідна. Вибірковий метод. Генеральна сукупність елементів. Вибірки та їх види в залежності від методів вибирання елементів. Вибірка властиво випадкова повторна і схема ”повернених куль”. Вибірка властиво випадкова без повторна і схема “неповернених куль”. Незсуненість, ефективність та обгрунтуваність як головні вимоги до вибіркових оцінок обраного параметра ознаки. Точкові вибіркові оцінки параметра. Довірчий інтервал вибіркової оцінки параметра. Оцінки якісних вибіркових ознак. Три типа задач вибіркового методу. Генеральною називають сукупність об’єктів, з якої зроблено вибірку. Об’єм генеральної сукупності позначають N. Вибірки бувають повторні (при яких відібраний об’єкт повертається до генеральної сукупності перед відбором іншого об’єкта) та безповторні (при яких взятий об’єкт до генеральної сукупності не повертається). Найчастіше використовуються безповторні вибірки.
Нехай знайдена за даними вибірки статистична оцінка Точкова статистична оцінка повинна задовольняти певним умовам, які сформулюємо у вигляді означень. Означення. Статистичну оцінку Означення. Статистичну оцінку Означення. Статистичну оцінку Відмітимо, що якщо дисперсія незсунутої оцінки при
ТРИ ТИПИ ЗАДАЧ ВИБІРКОВОГО МЕТОДА.
1) Для заданих об’ємові вибірки та довірчому інтервалі знайти надійність оцінки (дано: 2) При заданих об’ємові вибірки та надійності оцінки знайти довірчий інтервал (дано: 3) При заданих надійності оцінки та довірчому інтервалі знайти необхідний об’єм вибірки (дано: Означення. Інтервал при оцінюванні частки якісної ознаки
Порівняння емпіричного та теоретичного законів розподілу. Вибір виду теоретичного закону, знаходження його параметрів та перевірка його узгодженості із емпіричними даними, як необхідні передумови для остаточного обрання теоретичного закону. Критерії узгодженості Пірсона Критичне значення (критична точка) Правило Пірсона. Щоб при заданому рівні значущості 1) припустити наявність певного закону розподілу, знайти його параметри та побудувати (записати) цей закон; 2) обчислити за цим законом теоретичні частоти Випадкові події. Класифікація подій. Класичне означення поняття ”Ймовірність”. Відносна частота(частість). Статистичне означення поняття “Ймовірність Випадковою подією, яка може настати (з’явитись) або не настати у даному випробуванні. Достовірною подією, яка обов’язково настає у даному випробуванні. U. Неможливою подією, яка не може настати у даному випробуванні. Неможливу подію позначатимемо V.
Попарно несумісними подіями (несумісними у сукупності), якщо у даному випробуванні ніякі дві з них не можуть настати разом (поява однієї із подій виключає появу будь-якої іншої). У супротивному випадку події називають сумісними. Єдино можливими подіями, якщо у даному випробуванні обов’язково настане хоча б одна із цих подій. Події утворюють повну групу, якщо вони єдино можливі та попарно несумісні. Дві події Події називаються рівноможливими, якщо вони мають однакові шанси до появи у даному випробуванні. Простір елементарних подій – усі єдино можливі, рівноможливі та несумісні події, які неможливо поділити на більш прості події. Імовірність події A дорівнює: P(A)= m/n деn - число (кількість) подій у просторі елементарних подій, а m - число наслідків (із простору елементарних подій), які сприяють появі події A. Означення. Нехай проводиться n випробувань (які можна повторювати при незмінних умовах необмежено). Частотою m(A) називається кількість випробувань (із n), в яких з’явилась подія A. Частістю (відносною частотою або часткою) w(A)=m(A)/n називається відношення частоти появи події A до загальної кількості випробувань. Статистичною імовірністю події A називають число, що характеризує можливості появи події і яке дорівнює: P(A)=lim w(A).
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.54.6 (0.07 с.) |
 і
і 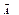 , які утворюють повну групу, називаються взаємно протилежними.
, які утворюють повну групу, називаються взаємно протилежними. ;
; .
. .
. і
і  ,
,  і
і  ,
,  .
.



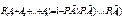 .
.
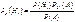 , i=1,2,…….,n
, i=1,2,…….,n
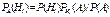 , де P(A) - повна імовірність.
, де P(A) - повна імовірність.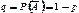 ). Тоді імовірність того, що подія A з’явиться m разів у n НПВ
). Тоді імовірність того, що подія A з’явиться m разів у n НПВ  знаходиться за формулою Бернуллі:
знаходиться за формулою Бернуллі:






 .
.
 .
.

 де a = const >0) називають розподіленою за законом Пуассона (закон рідкісних подій).
де a = const >0) називають розподіленою за законом Пуассона (закон рідкісних подій).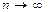 необмежено наближається до нормального.
необмежено наближається до нормального. ,
,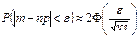 ,
,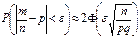

 справедлива нерівність:
справедлива нерівність: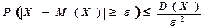
 ,або
,або 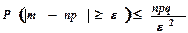 ;
; - частості (частки) появи події A в серії із n НПВ:
- частості (частки) появи події A в серії із n НПВ: , або
, або 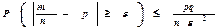
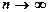 збігається за імовірністю до p = P(A) - імовірності появи події у кожному окремому випробуванні:
збігається за імовірністю до p = P(A) - імовірності появи події у кожному окремому випробуванні:

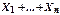 при
при 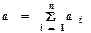 і дисперсією
і дисперсією 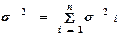
 є точковою оцінкою невідомого параметра
є точковою оцінкою невідомого параметра  . Означення. Статистичною (точковою) оцінкою невідомого параметра випадкової величини X генеральної сукупності (теоретичного розподілу X) називають функцію від випадкових величин (результатів вибірки), що спостерігаються.
. Означення. Статистичною (точковою) оцінкою невідомого параметра випадкової величини X генеральної сукупності (теоретичного розподілу X) називають функцію від випадкових величин (результатів вибірки), що спостерігаються. параметра називають незсунутою, якщо
параметра називають незсунутою, якщо  . Оцінку
. Оцінку  називають зсунутою, якщо ця рівність не виконується.
називають зсунутою, якщо ця рівність не виконується. параметра
параметра  називають ефективною, якщо вона при заданому об’ємі вибірки n має найменшу можливу дисперсію.
називають ефективною, якщо вона при заданому об’ємі вибірки n має найменшу можливу дисперсію. параметра
параметра  називають обгрунтованою (значимою, показною, репрезентативною), якщо вона при
називають обгрунтованою (значимою, показною, репрезентативною), якщо вона при  прямує за імовірністю до оцінюваного параметра.
прямує за імовірністю до оцінюваного параметра. прямує до нуля, то оцінка буде і обгрунтованою.
прямує до нуля, то оцінка буде і обгрунтованою. і
і  ; визначається
; визначається  ).
). і
і  ; визначається
; визначається  та
та  або
або  ).
). і
і  ; знаходиться
; знаходиться  ).
). називають довірчим, якщо він покриває невідомий параметр
називають довірчим, якщо він покриває невідомий параметр  із заданою надійністю
із заданою надійністю  .
. повторної,
повторної, убезповторної.
убезповторної. знаходиться за відповідними таблицями (або за спеціальними функціями Excel).
знаходиться за відповідними таблицями (або за спеціальними функціями Excel). перевірити основну гіпотезу
перевірити основну гіпотезу  : генеральна сукупність розподілена за певним законом, потрібно:
: генеральна сукупність розподілена за певним законом, потрібно: для кожної варіанти
для кожної варіанти  (або інтервалу варіант);
(або інтервалу варіант);


