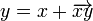Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кривые в евклидовом пространствеСтр 1 из 4Следующая ⇒
Вопросы к экзамену по векторному и тензорному анализу Кривые в евклидовом пространстве Формулы Френе для плоской кривой Кривизна кривой. Длина кривой В дифференциальной геометрии, кривизна́ — собирательное название ряда количественных характеристик (скалярных, векторных, тензорных), описывающих отклонение того или иного геометрического «объекта» (кривой, поверхности, риманова пространства и т. д.) от соответствующих «плоских» объектов (прямая, плоскость, евклидово пространство и т. д.). Длина кривой (или, что то же, длина дуги кривой) в метрическом пространстве — числовая характеристика протяжённости этой кривой. Для евклидова пространства длина отрезка кривой определяется как точная верхняя грань длин вписанных в кривую ломаных.
Пусть непрерывная кривая γ задана параметрически:
Где
Соединив точки кривой Всякая непрерывная кривая имеет длину, конечную или бесконечную. Если все функции в (1) являются функциями ограниченной вариации, то длина кривой существует и конечна. В математическом анализе выводится формула для вычисления длины s отрезка кривой, заданной уравнениями (1), при условии, что все три функции непрерывно дифференцируемы:
Простые поверхности в евклидовом пространстве Поверхности определяется как множество точек, координаты которых удовлетворяют определённому виду уравнений:
Если функция F(x,y,z) непрерывна в некоторой точке и имеет в ней непрерывные частные производные, по крайней мере одна из которых не обращается в нуль, то в окрестности этой точки поверхность, заданная уравнением (1), будет правильной поверхностью. Помимо указанного выше неявного способа задания поверхность может быть определена явно, если одну из переменных, например z, можно выразить через остальные:
Также существует параметрический способ задания. В этом случае поверхность определяется системой уравнений:
Касательная плоскость Пусть имеется поверхность, заданная уравнением F(x,y,z)=0. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку
называется касательной плоскостью к поверхности в точке M0 Если поверхность задана уравнением F(x,y,z)=0 то уравнение касательной плоскости к этой поверхности в точке М0:
Уравнение нормали в этой точке:
Длина кривой, заданной на поверхности Первая квадратичная форма поверхности Первая квадратичная форма или метрический тензор поверхности ― квадратичная форма от дифференциалов координат на поверхности, которая определяет внутреннюю геометрию поверхности в окрестности данной точки. Знание первой квадратичной формы достаточно для вычисления длин дуг, углов между кривыми, площади областей на поверхности. Пусть поверхность задана уравнением r = r(u,v),
где u и v ― внутренние координаты на поверхности; dr = rudu + rvdv
― дифференциал радиус-вектора r вдоль выбранного направления смещения из точки M в бесконечно близкую точку M'. Квадрат главной липшицевой части приращения длины | MM' | выражается квадратом дифференциала dr:
и называется первой основной квадратичной формой поверхности. Коэффициенты первой квадратичной формы обычно обозначают через
или в тензорных символах dr2 = g1,1du2 + 2g1,2dudv + g2,2dv2.
Тензор gi,j называется основным, или метрическим, тензором поверхности. Производная по направлению В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления. Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению. Рассмотрим функцию
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора e. Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате. Градиент скалярного поля Пусть задано скалярное поле U = f(x, y, z). Градиентом скалярного поля U = f(x, y, z) в точке M(x, y, z) называют вектор
Если функция U = f(x, y, z) имеет частные производные U'x, U'y, U'z в каждой точке некоторой области, то скалярное поле порождает в этой области векторное поле Обозначает направление наибольшего возрастания функции. Коэффициенты Ламе Выпишем дифференциал дуги в криволинейных координатах в виде (используется правило суммирования Эйнштейна):
Принимая во внимание ортогональность систем координат (
где
Положительные величины Тензор римановой метрики, записанный в координатах qi, представляет из себя диагональную матрицу, на диагонали которой стоя́т квадраты коэффициентов Ламе:
Градиент
где Hi — коэффициенты Ламе. Дивергенция
Градиент Коэффициенты Ламе:
Отсюда:
Дивергенция Коэффициенты Ламе:
Отсюда:
Ротор
где Hi — коэффициенты Ламе. Градиент Коэффициенты Ламе:
Отсюда:
Дивергенция Коэффициенты Ламе:
Отсюда:
Аффинное пространство Аффинное пространство — служит обобщением аффинных свойств евклидова пространства. Во многом схоже с векторным пространством, но в отличие от последнего, точки в аффинном пространстве являются равноправными. В частности в аффинном пространстве нет понятия нулевой точки или начала отсчёта. В аффинном пространстве возможно вычитать друг из друга точки и получать векторы так называемого присоединенного пространства; также возможно прибавлять вектор к точке и получать другую точку, но нельзя складывать точки друг с другом Определение Аффинное пространство над полем Если поле § Элементы A называются точками аффинного пространства § Пространство V называется пространством присоединенным к A § Образ действия § Для двух точек § Размерность пространства A определяется равной размерности присоединенного пространства V. 28. Преобразования базиса 29. Ковариантный тензор 30. Контрвариантный тензор Вопросы к экзамену по векторному и тензорному анализу Кривые в евклидовом пространстве
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 476; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.60 (0.02 с.) |

 (1)
(1) Рассмотрим всевозможные разбиения интервала значений параметра [a,b] на m отрезков:
Рассмотрим всевозможные разбиения интервала значений параметра [a,b] на m отрезков: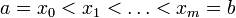
 отрезками прямых, мы получим ломаную линию. Тогда длина отрезка кривой определяется как точная верхняя грань суммарных длин всех таких ломаных.
отрезками прямых, мы получим ломаную линию. Тогда длина отрезка кривой определяется как точная верхняя грань суммарных длин всех таких ломаных.





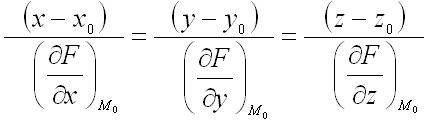


 от n аргументов в окрестности точки
от n аргументов в окрестности точки  Для любого единичного вектора
Для любого единичного вектора  определим производную функции f в точке X0 по направлению e следующим образом
определим производную функции f в точке X0 по направлению e следующим образом



 при
при  ) это выражение можно переписать в виде
) это выражение можно переписать в виде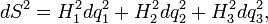

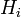 , зависящие от точки пространства, именуются коэффициентами Ламе или масштабными коэффициентами. Коэффициенты Ламе показывают, сколько единиц длины содержится в единице координат данной точки и используются для преобразования векторов при переходе от одной системы координат к другой.
, зависящие от точки пространства, именуются коэффициентами Ламе или масштабными коэффициентами. Коэффициенты Ламе показывают, сколько единиц длины содержится в единице координат данной точки и используются для преобразования векторов при переходе от одной системы координат к другой.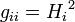 gij = 0 для i ≠ j
gij = 0 для i ≠ j



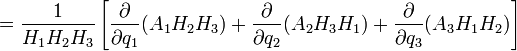 , где Hi — коэффициенты Ламе.
, где Hi — коэффициенты Ламе. .
.
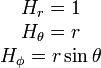 .
.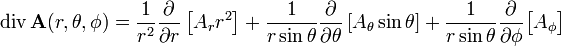

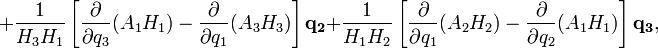
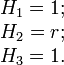

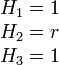 .
.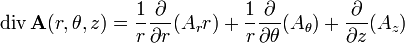
 — множество A со свободным транзитивным действием аддитивной группывекторного пространства V над полем
— множество A со свободным транзитивным действием аддитивной группывекторного пространства V над полем 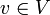 на
на 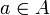 обозначается a + v
обозначается a + v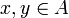 через
через  обозначается такой вектор из V, что
обозначается такой вектор из V, что