Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механическая система от внешних и внутренних сил. Первое свойство внутренних сил в механической системе.Стр 1 из 5Следующая ⇒
Билет 4. Механическая система от внешних и внутренних сил. Первое свойство внутренних сил в механической системе. Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных. Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.
Внутренними называются силы, действующие на точки системы со стороны других точек или тел этой же системы. Будем обозначать внешние силы символом -
Теоре́ма о движе́нии це́нтра масс (це́нтра ине́рции) системы — одна из общих теорем динамики, является следствием законов Ньютона утверждает, что ускорение центра масс механической системы не зависит от внутренних сил, действующих на тела системы, и связывает это ускорение с внешними силами, действующими на систему. Идеальные связи — класс связей, удовлетворяющих следующему условию: суммарная возможная работа всех реакций этих связей на любых возможных перемещениях равна нулю. Аналитически сформулированное выше условие идеальности для системы материальных точек может быть сформулировано так:
где Билет 5. Теорема об изменении количества движения механической системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает количество движенияс импульсом внешних сил, действующих на тела, составляющие систему. В качестве системы, о которой идёт речь в теореме, может выступать любая механическая система, состоящая из любых тел Формулировка теоремы Количеством движения (импульсом) механической системы называют величину, равную сумме количеств движения (импульсов) всех тел, входящих в систему. Импульс внешних сил, действующих на тела системы, — это сумма импульсов всех внешних сил, действующих на тела системы. Выражение главного вектора сил. принцип Даламбера Рассмотрим плоскую систему сил (F 1, F 2,..., F n),действующих на твердое тело в координатной плоскости Oxy.
Главным вектором системы сил называется вектор R, равный векторной сумме этих сил: R = F 1 + F 2 +... + F n = Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.
Принцип Даламбера. Все методы решения задач динамики, которые мы до сих пор рассматривали, основываются на уравнениях, вытекающих или непосредственно из законов Ньютона, или же из общих теорем, являющихся следствиями этих законов. Однако, этот путь не является единственным. Оказывается, что уравнения движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет, как мы увидим, найти более эффективные методы решения соответствующих задач. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Даламбера. Пусть мы имеем систему, состоящих из n материальных точек. Выделим какую-нибудь из точек системы с массой Введем в рассмотрение величину
имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки(иногда даламберовой силой инерции). Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам
Это выражение выражает принцип Даламбера для одной материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает Повторяя проделанные высшее рассуждения по отношению к каждой из точек системы, придем к следующему результату, выражающему принцип Даламбера для системы: если в любой момент времени к каждой из точек системы, кроме фактически действующих на ней внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно будет применять все уравнения статики.
Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия; что делает единообразный подход к решению задач и обычно намного упрощает соответствующие расчёты. Кроме того, в соединении с принципом возможных перемещений, который будет рассмотрен в следующей главе, принцип Даламбера позволяет получить новый общий метод решения задач динамики. Применяя принцип Даламбера, следует иметь в виду, что на точку механической системы, движение которой изучается, действуют только внешние и внутренние силы Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систе6му. Тогда на основании принципа Даламбера должно быть:
Введём обозначения:
Величины
Применение уравнений (1), вытекающих из принципа Даламбера, упрощает процесс решения задач, т.к. эти уравнения не содержат внутренних сил. В проекциях на оси координат эти равенства дают уравнения, аналогичные соответствующим уравнениям статики. Чтобы пользоваться этими уравнениями при решении задач, надо знать выражение главного вектора и главного момента сил инерций.
Билет 6. Формулировка теоремы Количеством движения (импульсом) механической системы называют величину, равную сумме количеств движения (импульсов) всех тел, входящих в систему. Импульс внешних сил, действующих на тела системы, — это сумма импульсов всех внешних сил, действующих на тела системы. Теорема об изменении количества движения системы утверждает: Изменение количества движения системы за некоторый промежуток времени равно импульсу внешних сил, действующих на систему, за тот же промежуток времени.
Билет №7 1. Центр масс системы материальных точек. Теорема о его движении Центр масс - геометрическая точка, характеризующая движение тела или системы частиц как целого.
Для случая непрерывного распределения масс:
Теорема о движении центра масс: произведение массы системы на ускорение её центра масс равно геометрической сумме всех действующих на систему внешних сил.
2. Возьмем абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 1). Разобьем тело на маленькие объемы с элементарными массами m1, m2,..., mn, находящиеся на расстоянии r1, r2,..., rn от оси.
При вращении твердого тела относительно неподвижной оси каждый из его элементарных объемов массами mi опишет окружность соответствующих радиусов ri; при этом объем будет иметь соответствующую линейную скорость vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
Используя выражение (1), получаем В качеcтве примера напишем формулу для плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения. Его энергия движения складывается из энергии поступательного движения и энергии вращения:
Билет №8 1. 2. Переносная и кориолисова сила инерции. Переносной силой инерции, действующей на материальную точку массы m в неинерциальной системе отсчета, называется сила, равная произведению массы этой материальной точки на взятое с обратным знаком ее переносное ускорение
Кориолисовой силой инерции, действующей на материальную точку массы m в неинерциальной системе отсчета, называется сила, равная произведению массы этой материальной точки на взятое с обратным знаком ее кориолисово ускорение Билет №9 1. Теорема обизменении кинетического момента механической системы относительно ее центра масс
2. Виртуальные (возможные) скорости точек механической системы Для одной материальной точки возможное перемещение вводится как бесконечно малое воображаемое перемещение, допускаемое связями в данный момент времени; это – векторная величина, совпадающая по направлению с возможной скоростью точки. Для механической системы возможное перемещение определяется как перемещение системы в бесконечно-близкое положение, допускаемое связями в данный момент времени. При этом каждая точка системы, как и в случае отдельной точки, получает возможное перемещение, совпадающее по направлению с ее возможной скоростью. Так для рычага (рис. 6.1) возможное перемещение определяется поворотом на бесконечно-малый угол Рис 6.1 Для кривошипно-ползунного механизма (рис. 6.2) возможное перемещение есть бесконечно малое смещение звеньев механизма из заданного положения. При этом точка направленное вдоль возможной скорости точки Число независимых возможных перемещений системы называется числом ее степеней свободы. Например, одну степень свободы имеет точка, перемещающаяся по прямой или по заданной криволинейной траектории. Также одну степень свободы имеет тело, вращающееся вокруг неподвижной оси. Для определения числа степеней свободы системы с голономными связями (Связи называются голономными, если они накладывают ограничения на положения тел и точек системы.) поступают следующим образом. Вначале у системы исключают одну степень свободы (для этого закрепляют точку, движущуюся по заданной линии, или закрепляют вращающееся тело). Если после этого подвижность системы будет полностью устранена значит, у системы одна степень свободы. Если же подвижность сохранится, то исключают еще одну степень свободы; и так далее до полного устранения подвижности системы (до полной остановки системы). Число таких исключений равно числу степеней свободы системы. Билет 10 1. Осевые и центробежные моменты инерции твердого тела. Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где: · mi — масса i -й точки, · ri — расстояние от i -й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где: · · · Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса — Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
где Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Центробежный момент инерции Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm. Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела. Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции. Билет 11 Билет 11 Билет 12 ПОТЕНЦИАЛЬНЫЕ СИЛЫ Поле сил, остающееся постоянным во времени, называется стационарным. В стационарном силовом поле сила, действующая на частицу, зависит только от ее положения. Работа, которую совершают силы поля при перемещении частицы из точки 1 в точку 2, зависит, вообще говоря, от траектории, по которой перемещается частица из начального положения в конечное. Вместе с тем, имеются стационарные силовые поля, в которых работа, совершаемая над частицами силами поля, не зависит от формы траектории между точками 1 и 2. Силы, обладающие таким свойством, называются потенциальными или консервативными, а соответствующее поле сил – потенциальным полем. Примером потенциальных сил являются упругие силы, сила тяжести.
Билет
1) Для внутренних сил механической системы имеет место свойство: главный вектор и главный момент внутренних сил механической системы равны нулю.
Это следует из того, что внутренние силы есть силы взаимодействия между точками системы, которые попарно равны и направлены в противоположные стороны. 2) Если все силы системы потенциальны, то обобщенные силы системы выражаются через потенциальную энергию системы как Qj = -дП / дqj, а уравнения Лагранжа второго рода запишутся в виде
Так как потенциальная энергия не зависит от обобщенных скоростей, то. Введем в рассмотрение функцию
которую называют функцией Лагранжа или кинетическим потенциалом. Тогда уравнения Лагранжа в случае потенциальных сил запишутся так:
Билет 16. 1. Tеорема об изменении кинетической энергии механической системы в дифференциальной форме Изменение кинетической энергии механической системы на некотором ее перемещении равно сумме работ внешних и внутренних сил, приложенных к точкам системы, на том же перемещении.
2. Удерживающие и стационарные связи Если функция
Если связь задаётся равенством, то говорят, что такая связь — удерживающая или двусторонняя:
Билет 17 1 Tеорема об изменении кинетической энергии механической системы Кинетической энергией системы называют сумму кинетических энергий всех тел, входящих в систему. Для определённой таким образом величины справедливо утверждение: Изменение кинетической энергии системы равно работе всех внутренних и внешних сил, действующих на тела системы.
2 Голономные связи Голоно́мная связь — механическая связь, налагающая ограничения только на положения (или перемещения) точек и тел системы. Математически выражается в виде равенства:
Билет 18 1.Принцип Эйлера-Даламбера для материальной точки Согласно данному принципу, для каждой i-той точки системы верно равенство 2 кинетическая энергия тела при плоском движении
Билет 19 Уравнения кинетостатики. Кинетостатика - раздел механики, в котором рассматриваются способы решения динамических задач с помощью аналитических или графических методов статики. В основе К. лежит Д'Аламбера принцип, согласно которому уравнения движения тел можно составлять в форме уравнений статики, если к фактически действующим на тело силам и реакциям связей присоединить силы инерции. Методы К. находят применение при решении ряда динамических задач, особенно в динамике машин и механизмов. уравнения кинетостатики для материальной точки:
где F, R, Ф - главные векторы активных сил, реакций связей и сил инерции; Fz, Rz, Фz- главные моменты активных сил, реакций связей и сил инерции относительно точки О1 Билет 20 Общее уравнение динамики. Общее уравнение динамики
Билет 21 Мощность пары сил Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело. Мощность пары сил:
где омега Z – проекция угловой скорости на ось вращения.
Билет 22 1.Прнцип виртуальных перемещений Если связь одна и описывается уравнением (2), физически ясно, что связь не нарушится, когда вектор виртуального перемещения
будет лежать в плоскости, касательной к поверхности связи, зафиксированной в данное мгновение времени. Математически это условие выражается как
где grad f - градиент функции (2) при фиксированном t, перпендикулярный поверхности связи в месте нахождения точки, равный
Учитывая выражения (3) и (5), раскрываем скалярное произведение в (4), получаем уравнение, которому должны удовлетворять проекции δxi, δyi, δzi виртуального перемещения δri, чтобы связь не нарушалась:
В вариационном исчислении бесконечно малые величины δri, δxi, δyi, δzi называются вариациями функций ri, xi, yi, zi. Изменения координат точек или уравнений связи при неизменном времени находятся синхронным варьированием, которое осуществляется согласно левым частям формул (4) и (6). То есть проекции δxi, δyi, δzi виртуального перемещения точки δr обращают в нуль первую вариацию уравнения связи при условии, что время не варьируется (синхронное варьирование):
Следовательно, виртуальное перемещение точки не характеризует ее движение, а определяет связь или, в общем случае, связи, наложенные на точку системы. Таким образом, виртуальные перемещения позволяют учесть эффект механических связей, не вводя реакции связей, как мы это делали раньше, и получать уравнения равновесия или движения системы в аналитическом виде, не содержащие неизвестных реакций связей. 2.Элементарная работа Элементарная работа силы равна скалярному произведению силы на дифференциал радиуса-вектора точки приложения силы. [ 2 ] Элементарная работа сил при этом зависит от выбора возможного перемещения системы. [ 3 ] Элементарная работа силы при вращении тела, на которое сила действуе
Билет 23 1. Принцип виртуальных перемещений в обобщенных координатах. Запишем принцип, выражая виртуальную работу активных сил системы в обобщенных координатах:
Так как на систему наложены голономные связи, вариации обобщенных координат не зависят между собой и не могут быть одновременно равны нулю. Поэтому последнее равенство выполнится только тогда, когда коэффициенты при δj (j = 1 ÷ s) одновременно обращаются в нуль, то есть
Таким образом, для равновесия материальной системы с голономными стационарными идеальными связями необходимо и достаточно, чтобы одновременно равнялись нулю все обобщенные силы системы по всем обобщенным координатам. Если силы, действующие на систему, являются потенциальными, то согласно (11) уравнения равновесия принимают вид
2.Работа силы на конечном перемещении
или
Билет 24 1.уравнение Лагранжа второго рода. Для вывода уравнений запишем принцип Даламбера-Лагранжа в обобщенных координатах в виде -Qju = Qj (j = 1 ÷ s). Принимая во внимание, что Фi = -miai = -midVi / dt, получаем:
Далее обобщенные силы инерции в левой части нужно выразить через кинетическую энергию(для систем с голономными связями обобщенные силы инерции равны):
Подставляя (2) в (1) получаем дифференциальное уравнение движения системы в обобщенных координатах, которое названо уравнением Лагранжа второго рода:
то есть, материальная система с голономными связями описывается уравнениями Лагранжа второго рода по всем s обобщенным координатам. Отметим важные особенности полученных уравнений. 1. Уравнения (3) - это система обыкновенных дифференциальных уравнений второго порядка относительно s неизвестных функций qj(t), полностью определяющих движение системы. 2. Число уравнений равно числу степеней свободы, то есть движение любой голономной системы описывается наименьшим числом уравнений. 3. В уравнения (3) не нужно включать реакции идеальных связей, что позволяет, находя закон движения несвободной системы, выбором обобщенных координат исключить задачу определения неизвестных реакций связей. 4. Уравнения Лагранжа второго рода позволяют указать единую последовательность действий для решения многих задач динамики, которую часто называют формализмом Лагранжа.
2. Условие относительного покоя материальной точки получают из динамического уравнения Кориолиса, подставив в это уравнение значения относительного ускорения и кориолисовой силы инерции равные нулю:
или
Билет 4. Механическая система от внешних и внутренних сил. Первое свойство внутренних сил в механической системе. Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных. Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1597; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.31.73 (0.169 с.) |
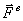 , а внутренние -
, а внутренние - 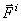 .
.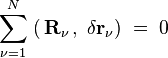 ,
,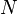 — число точек, входящих в систему,
— число точек, входящих в систему, 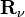 — равнодействующая реакций связей, приложенных к
— равнодействующая реакций связей, приложенных к 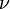 -й точке,
-й точке, 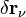 — возможное перемещение данной точки (круглыми скобками обозначено скалярное произведение векторов).
— возможное перемещение данной точки (круглыми скобками обозначено скалярное произведение векторов). F i.
F i.
 . Под действием приложенных к ней внешних и внутренних сил
. Под действием приложенных к ней внешних и внутренних сил  и
и  (в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение
(в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение 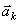 .
.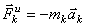 ,
,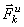 , то полученная система сил будет уравновешенной, т.е. будет
, то полученная система сил будет уравновешенной, т.е. будет .
. . Перенося здесь член
. Перенося здесь член 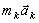 в правую часть равенства и придем к последнему соотношению.
в правую часть равенства и придем к последнему соотношению. . Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют (иначе, эти точки находились бы в покое или двигались без ускорений и тогда не было бы и самих сил инерции). Введение сил инерции - это лишь приём, позволяющий составлять уравнения динамики с помощью более простых методов статики.
. Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют (иначе, эти точки находились бы в покое или двигались без ускорений и тогда не было бы и самих сил инерции). Введение сил инерции - это лишь приём, позволяющий составлять уравнения динамики с помощью более простых методов статики.


 и
и  представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств:
представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств: ,
, 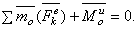 (1)
(1)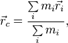 где
где 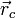 — радиус-вектор центра масс,
— радиус-вектор центра масс, 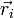 — радиус-вектор i -й точки системы,
— радиус-вектор i -й точки системы, 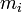 — масса i -й точки.
— масса i -й точки.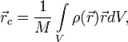
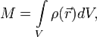 где
где 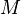 — суммарная масса системы,
— суммарная масса системы, 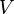 — объём,
— объём, 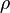 — плотность.
— плотность.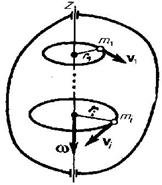
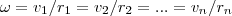 (1)
(1)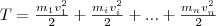
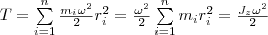
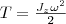 (2)
(2) 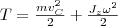




 вокруг точки опоры. При этом возможное перемещение
вокруг точки опоры. При этом возможное перемещение 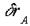 точки
точки 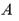 направлено перпендикулярно рычагу, т.е. в сторону ее возможной скорости.
направлено перпендикулярно рычагу, т.е. в сторону ее возможной скорости.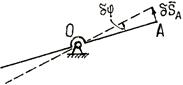 рис 6.2
рис 6.2 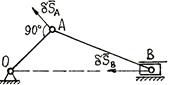
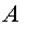 имеет возможное перемещение, направленное вдоль ее возможной скорости, т.е. перпендикулярно кривошипу
имеет возможное перемещение, направленное вдоль ее возможной скорости, т.е. перпендикулярно кривошипу 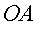 ; а точка
; а точка 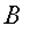 имеет возможное перемещение,
имеет возможное перемещение,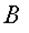 .
.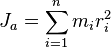 ,
,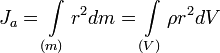 ,
,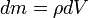 — масса малого элемента объёма тела
— масса малого элемента объёма тела 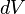 ,
, — расстояние от элемента
— расстояние от элемента 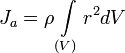
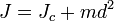 ,
,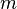 — полная масса тела.
— полная масса тела.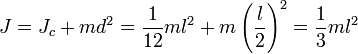
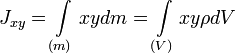
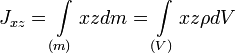
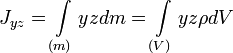

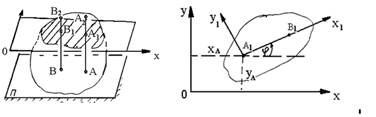 Рассмотрим сечение тела какой-нибудь плоскостью OXY, параллельной неподвижной плоскости П (рис.1).При плоскопараллельном движении все точки тела, лежащие на прямой
Рассмотрим сечение тела какой-нибудь плоскостью OXY, параллельной неподвижной плоскости П (рис.1).При плоскопараллельном движении все точки тела, лежащие на прямой 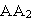 , перпендикулярной к сечению, т.е. к плоскости П, движутся тождественно. Поэтому для изучения движения всего тела достаточно изучить, как движется сечение тела в плоскости OXY. В дальнейшем будем плоскость OXY совмещать с плоскостью рисунка, а вместо всего тела изображать только его сечение. Положение сечения в плоскости OXY определяется положением какого-нибудь проведенного в этом сечении отрезка АВ (рис.2). Положение отрезка АВ можно определить, зная координаты
, перпендикулярной к сечению, т.е. к плоскости П, движутся тождественно. Поэтому для изучения движения всего тела достаточно изучить, как движется сечение тела в плоскости OXY. В дальнейшем будем плоскость OXY совмещать с плоскостью рисунка, а вместо всего тела изображать только его сечение. Положение сечения в плоскости OXY определяется положением какого-нибудь проведенного в этом сечении отрезка АВ (рис.2). Положение отрезка АВ можно определить, зная координаты 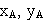 точки А и угол
точки А и угол 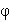 , который от-резок АВ образует с осью x. Точку А, выбранную для определения положения сечения, называют полюсом. При движении тела величины
, который от-резок АВ образует с осью x. Точку А, выбранную для определения положения сечения, называют полюсом. При движении тела величины 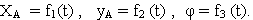 (1.74)
Уравнения определяющие закон происходящего движения, называются уравнениями плоскопараллельного движения твердого тела.
2.Главный момент всех внутренних сил системы(относительно всякого выбранного центра) в любой момент времени равен нулю (MOi=0).M-вектор.
(1.74)
Уравнения определяющие закон происходящего движения, называются уравнениями плоскопараллельного движения твердого тела.
2.Главный момент всех внутренних сил системы(относительно всякого выбранного центра) в любой момент времени равен нулю (MOi=0).M-вектор.
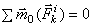 или
или 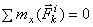 .
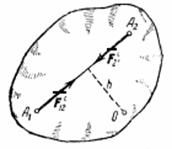
Уравновешенными внутренние силы будут тогда, когда рассматриваемая система представляет собою абсолютно
твердое тело. Действительно, если взять произвольный центр О, то из рис. видно, что
.
Уравновешенными внутренние силы будут тогда, когда рассматриваемая система представляет собою абсолютно
твердое тело. Действительно, если взять произвольный центр О, то из рис. видно, что 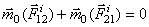 .
.
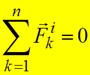
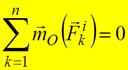 .
.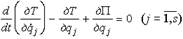
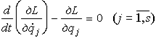
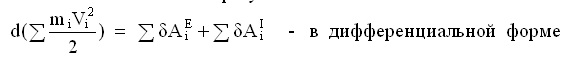
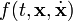 зависит явно от времени, то говорят, что связь — нестационарная или реономная; если же эта функция не зависит явно от времени, то говорят, что эта связь — стационарная или склерономная.
зависит явно от времени, то говорят, что связь — нестационарная или реономная; если же эта функция не зависит явно от времени, то говорят, что эта связь — стационарная или склерономная.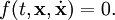

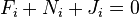 , где
, где  — действующая на эту точку активная сила,
— действующая на эту точку активная сила, 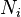 — реакция наложенной на точку связи,
— реакция наложенной на точку связи, 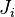 — сила инерции, численно равная произведению массы
— сила инерции, численно равная произведению массы 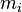 точки на её ускорение
точки на её ускорение 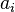 и направленная противоположно этому ускорению (
и направленная противоположно этому ускорению (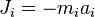 )
)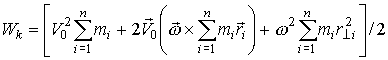
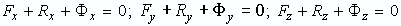
 – при движении системы с идеальными связями в каждый данный момент времен сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю. Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы. Дает общий метод решения задач динамики. Последовательность составления: а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные перемещения; в) составляют уравнения принципа возможных перемещений, считая систему находящейся в равновесии.
– при движении системы с идеальными связями в каждый данный момент времен сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю. Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы. Дает общий метод решения задач динамики. Последовательность составления: а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные перемещения; в) составляют уравнения принципа возможных перемещений, считая систему находящейся в равновесии.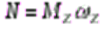 ,
,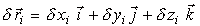
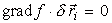
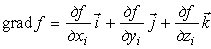

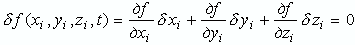

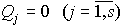

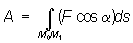

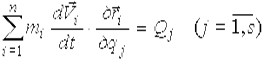 (1)
(1) (2)
(2) (3)
(3)