
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем линейных алгебраических уравнений
Методы решения систем линейных алгебраических уравнений делятся на две группы. К первой группе принадлежат так называемые точные, или прямые, методы - алгоритмы, позволяющие получить решение системы за конечное число арифметических действий. Сюда относятся известное правило Крамера нахождения решения с помощью определителей, метод Гаусса (метод исключений) и метод прогонки [13]. Правило Крамера при реализации на ЭВМ не применяется ввиду значительно большего по сравнению с методом Гаусса числа арифметических действий. Метод Гаусса используется при решении систем до порядка 103. Метод прогонки применяется для решения важного класса специальных систем линейных уравнений с трехдиагональной матрицей, часто возникающей в практических приложениях. Вторую группу составляют приближенные методы, в частности, итерационные методы решения систем линейных алгебраических уравнений, позволяющие решать системы до порядка 106 [1], [4], [7], [13]. Включенные в настоящий цикл две лабораторные работы посвящены решению задач линейной алгебры итерационными методами с использованием стандартных процедур.
Решение систем линейных алгебраических уравнений методом Гаусса
Рассматривается система линейных уравнений n -го порядка
.....
что в векторном виде записывается как Суть метода исключения по главным элементам (метод Гаусса) заключается в следующем. Находится наибольший по абсолютной величине коэффициент
......
из которого легко находятся неизвестные Следует отметить, что если матрица заданной системы вырожденная, то перед исключением некоторой неизвестной главный элемент Мерой обусловленности матрицы
где Лабораторная работа № 11
В ходе выполнения работы студенты должны найти решение системы линейных уравнений с n неизвестными, заданной матрицей коэффициентов 1) с помощью преподавателя определить систему уравнений, которую нужно решить; 2) для решения системы уравнений разработать программу на языке C, использующую подпрограмму-функцию GAUSS из файла GAUSS.CPP. Данная функция имеет следующие параметры: - a - матрица коэффициентов системы уравнений размера - - - В разрабатываемой программе должна быть описана константа n max, равная максимальным размерам используемых матриц и векторов. Функция GAUSS в качестве значения типа а) 0 - в случае нормального завершения процесса вычисления; б) 1 - в случае вырожденности матрицы а; в) 2 - если г) 3 - если Провести вычисления с использованием разработанной программы и исследовать обусловленность задачи с использованием пакета Matlab, при этом для определения числа обусловленности матрицы A рекомендуется использовать функцию cond(A) [14]. Кроме того, для проверки получаемых результатов можно провести вычисления с помощью пакетов Matlab и Derive [15].
Решение систем линейных алгебраических уравнений методом простой Итерации
Рассматривается система уравнений вида
где
где k =1, 2, … Доказана теорема, что если норма
которое может быть использовано для принятия решения об останове итерационного процесса при выполнении условия
где
Лабораторная работа № 12
В работе студенты должны найти решение системы линейных уравнений с n неизвестными, заданной матрицей коэффициентов 1) с помощью преподавателя определить систему уравнений, которую нужно решить. Привести исходную систему к виду (2.3), пригодному для использования метода простых итераций; 2) задать необходимую точность получения результата (количество знаков мантиссы числа); 3) разработать программу решения задачи на языке С с использованием подпрограммы-функции MITER из файла MITER.CPP. Функция MITER имеет следующие параметры: - - - - - - it - выходной параметр, равный количеству произведенных итераций, тип int. В качестве значения функции типа а) 0 - все нормально, получено решение б) 1 - не выполняются условия сходимости итерационного процесса; в) 2 - размер г) 3 - значение Константа 4) произвести вычисления с использованием разработанной программы и построить график зависимости числа итераций от задаваемой точности.
|
||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.210.17 (0.016 с.) |

 (2.1)
(2.1) ,
,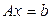 .
. . Для исключения
. Для исключения 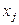 из i -го уравнения
из i -го уравнения  необходимо умножить k -е уравнение на
необходимо умножить k -е уравнение на  и вычесть его из i -го уравнения, после чего процесс повторяется для исключения другого неизвестного из оставшихся
и вычесть его из i -го уравнения, после чего процесс повторяется для исключения другого неизвестного из оставшихся  -1 уравнений и т. д. В результате система (2.1) приводится к треугольному виду
-1 уравнений и т. д. В результате система (2.1) приводится к треугольному виду
 (2.2)
(2.2) ,
, . Процесс приведения системы к виду (2.2) называется прямым ходом, а нахождение неизвестных
. Процесс приведения системы к виду (2.2) называется прямым ходом, а нахождение неизвестных  называют величину
называют величину  , где
, где 
 - норма матрицы
- норма матрицы  ,
, - i -е собственное число матрицы
- i -е собственное число матрицы  большая, то матрица
большая, то матрица  и вектором свободных членов
и вектором свободных членов 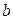 , методом Гаусса. Выполнение работы состоит из следующих этапов:
, методом Гаусса. Выполнение работы состоит из следующих этапов: , тип
, тип 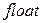 ;
;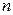 , тип
, тип  - выходной вектор результата решения размера
- выходной вектор результата решения размера 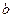 ), тип
), тип 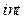 .
.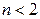 ;
;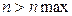 .
.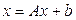 , (2.3)
, (2.3)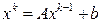 , (2.4)
, (2.4) , то система уравнений (2.3) имеет единственное решение
, то система уравнений (2.3) имеет единственное решение  и итерации (2.4) сходятся к решению со скоростью геометрической прогрессии [13]. Для оценки погрешности k -го приближения широко применяется неравенство
и итерации (2.4) сходятся к решению со скоростью геометрической прогрессии [13]. Для оценки погрешности k -го приближения широко применяется неравенство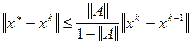 , (2.5)
, (2.5)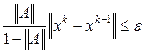 ,
,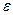 - некоторая заданная погрешность вычислений.
- некоторая заданная погрешность вычислений. - матрица коэффициентов преобразованной к виду (2.3) системы уравнений размера
- матрица коэффициентов преобразованной к виду (2.3) системы уравнений размера 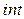 ;
; - количество знаков после запятой в мантиссе результата, остающихся после округления, тип
- количество знаков после запятой в мантиссе результата, остающихся после округления, тип 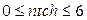 ;
;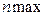 должна быть задана при разработке головной программы аналогично тому, как это делается при выполнении лабораторной работы № 11;
должна быть задана при разработке головной программы аналогично тому, как это делается при выполнении лабораторной работы № 11;


