
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обчислення машинного епсилон. ⇐ ПредыдущаяСтр 3 из 3
Точність плаваючої арифметики можна характеризувати за допомогою машинного епсилон, тобто найменшого числа з плаваючою комою, такого що 1 де Хоч це означення виділяє як машинне ε єдине число плаваючої системи, не так вже й важливо використовувати його точне значення. Воно використовується звичайно в програмах таким чином, що може відрізнятися від свого точного значення декількома степенями 2, не викликаючи при цьому серйозних труднощів. Існує декілька методів для наближеного обчислення значення ε, таким чином програма може визначити точність машини, на якій вона виконується, під час свого виконання. Метод, яким можна обчислити наближення, котре відрізняється від ε щонайбільше множником 2, ілюструється наступним сегментом фортранної програми: EPS = 1. 10 EPS = 0.5*EPS EPS P1 = EPS + 1. IF (EPS P1.GT.1) GO TO 10
Поняття про матриці. Система чисел розташованих в прямокутній таблиці із “ т ” рядків та “ n ” стовпців називається матрицею розміру т
Числа аij, де i – номер рядка; j – номер стовпця – називають елементами матриці. Для матриці часто використовують скорочену форму запису
або Якщо матриця складається з одного рядка (тобто має порядок 1
Якщо ж матриця складається з одного стовпця (т
Якщо число рядків і стовпців однакове, то матриця називається квадратною (тобто т = n). Якщо т ≠ n, то – прямокутною. Число (скаляр) можна розглядати як матрицю 1 Головною діагоналлю квадратної матриці називають діагональ, що проходить через верхній лівий і нижній правий кути, тобто сукупність елементів вигляду аіі, де Квадратна матриця вигляду
називається діагональною матрицею. Якщо при цьому α і = 1, то матриця (2) називається одиничною і позначається буквою Е, тобто
Матриця, всі елементи якої рівні нулю, називають нульовою і позначається через нуль. При необхідності вказати число рядків і стовпців використовують позначення 0 mn. Дві матриці вважається рівними, якщо вони одного і того ж типу (розміру), тобто мають однакове число рядків і стовпців, і відповідні елементи їх рівні А = В аij = bij
Додавання та віднімання матриць однакового розміру.
Добуток матриці А на число α (або навпаки) – це матриця, елементи якої одержуються множенням всіх елементів матриці А на число α
Добуток матриць. Нехай А та В матриці порядків т
це матриця С розміру т
Правило множення: щоб одержати елемент, що стоїть в і – му рядку та j – му стовпці добутку двох матриць, необхідно елементи і – го рядка першої матриці помножити на відповідні елементи j – го стовпця другої матриці і одержані добутки додати. Слід наголосити, що множення А на В допустиме (тобто добуток А ∙ В існує), якщо число стовпців А дорівнює числу рядків В. Приклад.
Якщо в матриці т
замінити рядки власними стовпчиками, то одержимо матрицю
розміру n
Метод послідовних наближень (метод Пікара). Нехай задано рівняння або права частина якого в прямокутнику х = х 0, у (х 0) = у 0 (2) Інтегруючи обидві частини рівняння від х 0 до х, одержимо: або Рівняння (1) заміняється інтегральним рівнянням (3). Інтегральне рівняння (3) задовольняє диференціальне рівняння (1) і початковій умові (2). Дійсно
Замінюючи в рівності (3) функцію у значенням у 0, одержимо перше наближення
Одержуємо послідовність функцій { уі (х) }, що збігається до функції у (х), яка є розв’язком диференціального рівняння у′ = f (х, у) у 1(х), у 2(х), у 3(х), …, уn (х) Приклад. Розв’язати методом Пікара диференціальне рівняння у′ = х 2 + у 2. Початкові умови х 0 = 0, у (х 0)= = у 0 = 0. Переходимо до інтегрального рівняння
або з врахуванням початкових умов
Одержимо послідовні наближення
Метод Пікара зручно застосовувати, якщо інтеграли в (4) вдається обчислювати через елементарні функції. Якщо ж права частина рівняння (1) більш складна, то ці інтеграли доводиться знаходити чисельними методами, і методом Пікара не досить зручний.
|
|||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.142.146 (0.008 с.) |
 ε > 1,
ε > 1, n.
n. (1)
(1) (
( ;
;  )
)


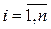 .
. (2)
(2)
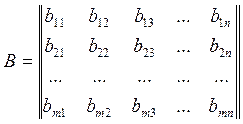


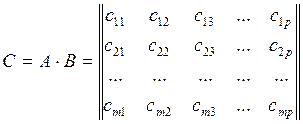
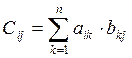 (
( )
) .
.
 (1)
(1) неперервна та має неперервну частинну похідну по у. Потрібно знайти розв’язок рівняння (1), що задовольняє початковій умові
неперервна та має неперервну частинну похідну по у. Потрібно знайти розв’язок рівняння (1), що задовольняє початковій умові (3)
(3)
 (4)
(4) ,
,




