Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие установившихся и переходных режимов работы элементов и систем автоматики ⇐ ПредыдущаяСтр 4 из 4
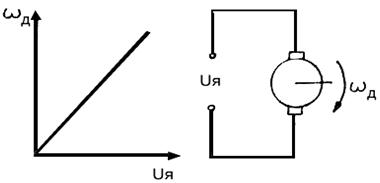
При приложении воздействия к какому либо объекту (элементу или системе автоматики) из-за инерционности объекта возникает переходный процесс, который через некоторое время заканчивается. После окончания переходного процесса объект работает в режиме, который называется установившимся. Например, если на электродвигатель подать напряжение питания, то после его разгона (переходного процесса) установится определенная частота wд вращения его вала (установившийся режим) (рис. 2.8.1). Установившиеся режимы бывают 2-х типов: статические и динамические. Если после окончания переходного процесса выходная величина объекта остается постоянной при постоянном воздействии, то такой установившийся режим является статическим.
Рис. 2.8.1 Переходный процесс и установившийся режим работы электродвигателя после подачи на него напряжения питания
Статический режим отражает статическая характеристика объекта.
Рис. 2.8.2 Статическая характеристика электродвигателя и поясняющая схема
Динамические установившиеся режимы могут возникать при постоянном воздействии на объект и воздействии, изменение которого носит установившийся характер. Примерами установившихся динамических режимов при постоянных воздействиях являются автоколебания, возникающие в нелинейных системах. Примером установившихся динамических режимов при установившемся воздействии является реакция линейного звена или линейной системы на гармоническое входное воздействие (см. частотные характеристики линейных систем и звеньев) и т. д. Типовые воздействия. Временные (переходные) и частотные Характеристики линейных систем и звеньев При эксплуатации на системы и их отдельные элементы (звенья) действуют различные внешние воздействия. Наиболее часто изучают реакцию систем и звеньев на типовые воздействия, являющиеся математическими моделями наиболее часто встречающихся реальных воздействий.
В качестве типовых используют следующие воздействия. 1. Ступенчатое воздействие:
x(t)= 1 (t)а при t ³ 0, (2.9.1)
где 1 (t) ¾ единичное ступенчатое воздействие; а - величина ступенчатого воздействия. 2. Импульсное воздействие (дельта-функция):
x(t) = d (t) = 0 при t « 0. (2.9.2)
При этом, согласно определению:
Дельта-функция связана с единичным ступенчатым воздействием: d (t) = 1I (t). (2.9.4)
3. Гармоническое воздействие: x(t) = Ах sinw t, (2.9.5) где Ах ¾ амплитуда; w¾ угловая частота.
Иногда используют и другие типовые воздействия.
Временные характеристики Реакция системы (звена) на единичное ступенчатое воздействие при нулевых начальных условиях называется переходной функцией. Переходная функция обычно обозначается h(t). Если ступенчатое входное воздействие неединичное 1 (t) × а, то ординаты переходной функции увеличиваются в а раз, что следует из принципа суперпозиции для линейных систем и звеньев. Реакция системы (звена) на импульсное воздействие (d - функцию) при нулевых начальных условиях называется импульсной переходной функцией или функцией веса.
Функция веса обычно обозначается W(t). Переходные функции и функции веса получают путем решения дифференциальных уравнений, описывающих системы (звенья) при ступенчатых и импульсных воздействиях, по их передаточным функциям и путем моделирования на ЭВМ. Они могут быть получены также экспериментально (импульсную переходную функцию получают как реакцию на короткий импульс).
Возможный вид переходных и импульсных переходных функций приведен на рис. 2.9.1 и 2.9.2.
Рис. 2.9.1 Возможный вид переходных функций
Рис. 2.9.2 Возможный вид импульсных переходных функций
Из (2.9.4) следует связь между переходной и импульсной переходной функциями: W(t) = h'(t); (2.9.6)
Учитывая, что изображение Лапласа L[ d (t)]= 1, следует взаимосвязь между импульсной переходной функцией, переходной функцией и передаточной функцией системы или звена:
L[w(t)]=w(p); (2.9.8) w (t)=L -1 [w(p)]; (2.9.9)
где L ¾ прямое преобразование Лапласа; L -1 ¾ обратное преобразование Лапласа.
Если на линейную систему (звено) подать гармоническое воздействие х(t)= =Ах sinw t, то после окончания переходного процесса на выходе звена установятся гармонические колебания у(t) = Aу sin ( w t + j ), где Ау ¾ амплитуда, j ¾ разность фаз между входным воздействием и выходной величиной (рис. 2.9.3).
Рис. 2.9.3 К определению частотных характеристик линейных звеньев Свойства линейных систем (звеньев) таковы, что частоты входных и выходных сигналов одинаковы. Амплитуда выходного сигнала при постоянной амплитуде входного сигнала и разность фаз между входным и выходным сигналами зависит только от частоты. Реакция системы (звена) на гармоническое воздействие характеризуется его частотными характеристиками. Амплитудной частотной характеристикой (АЧХ) называется зависимость отношения амплитуд выходного и входного гармонических сигналов от частоты в установившемся режиме:
Фазовой частотной характеристикой (ФЧХ) называется зависимость разности фаз j(w) между входным и выходным сигналами от частоты в установившемся режиме. Для теоретического получения АЧХ и ФЧХ систем и звеньев используют их частотные передаточные функции, поскольку модуль А( w ) частотной передаточной функции системы или звена является АЧХ этой системы или звена, а аргумент j ( w ) частотной передаточной функции системы или звена является ФЧХ этой системы или звена. Частотные характеристики систем и звеньев при необходимости получают также экспериментально. По результатам расчетов или эксперимента строятся графики АЧХ и ФЧХ.
Возможный вид графиков АЧХ и ФЧХ, например, для звена, описываемого дифференциальным уравнением 2-го порядка (звена 2-го порядка) приведен ниже.
Рис. 2.9.4 Возможный вид графиков АЧХ и ФЧХ
Кроме того, часто строится совместная амплитудно-фазовая частотная характеристика (АФЧХ) в координатах U( w ) и jV( w ):
W(j w ) = U( w ) + jV( w ) = A( w ) e j j ( w ). (2.9.13) Из выражения (2.9.13) следует, что АФЧХ может быть построена двумя способами. Первый способ заключается в предварительном разделении частотной передаточной функции на действительную U( w ) и мнимую jV( w ) части и затем расчете координат точек АФЧХ при изменении частоты от 0 до ¥ и построении графика по этим точкам. Второй способ заключается в расчете значений модуля А( w ) и аргумента j(w) при изменении частоты от 0 до ¥. Затем график АФЧХ строится по значениям А( w ) и j ( w ). При этом длина вектора, соединяющего начало координат с графиком равна А( w ), а угол поворота от действительной оси U равен j ( w ). График АФЧХ называют годографом АФЧХ.
Очень часто графики АЧХ и ФЧХ строятся в логарифмическом масштабе в функции от lgw. График АЧХ, построенный в логарифмическом масштабе, называют логарифмической амплитудной характеристикой (ЛАХ), график ФЧХ, построенный в логарифмическом масштабе, называют логарифмической фазовой характеристикой (ЛФХ). Перевод значений АЧХ в значения ЛАХ осуществляется следующим образом:
L( w ) = 20 lg A( w ), дБ. (2.9.14)
Таким образом, единицей измерения амплитуды является децибел. ФЧХ j(w)не логарифмируется. Единицей измерения lgw является декада, что соответствует увеличению частоты в 10 раз. На графике по оси lgw чаще всего записывают значения самой частоты w (см. рис. 2.9.6 и 2.9.7). Поскольку lg0 = - ¥, точка для w = 0 показывается условно (без соблюдения масштаба) или вообще не показывается. Применение ЛАХ обусловлено возможностью их построения почти без расчетов в виде асимптот к действительным значениям ЛАХ, которые меняют свой наклон при частотах, называемых сопрягающими. Кроме того, построение общей ЛАХ цепи последовательно соединенных звеньев можно провести сложением ЛАХ отдельных звеньев на графике. На рис. 2.9.6 и 2.9.7 показан возможный вид ЛАХ и ЛФХ взятого в качестве примера звена второго порядка. Сопрягающие частоты обозначены wС.1 и wС.2.
Рис. 2.9.6 Возможный вид ЛАХ
Рис. 2.9.7 Возможный вид ЛФХ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.239.46 (0.026 с.) |

 0 при t < 0;
0 при t < 0; ¥ при t = 0;
¥ при t = 0; . (2.9.3)
. (2.9.3)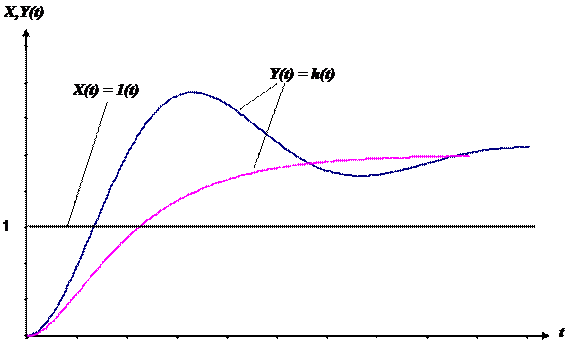

 . (2.9.7)
. (2.9.7)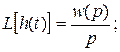 (2.9.10)
(2.9.10) (2.9.11)
(2.9.11)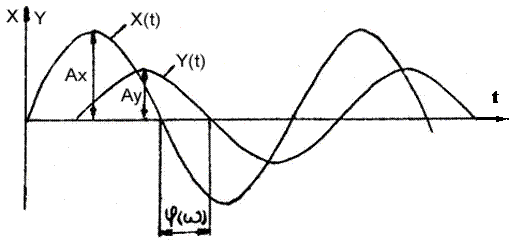
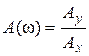 . (2.9.12)
. (2.9.12)