I Выполнение операций в АЛУ для чисел с фиксированной точкой

АЛУ для выполнения операций сложения и вычитания над числами с фиксированнойточкой.

Любое число с фиксированной точкой имеет 7 разрядов

Пример

x-y

5-3

Прямой код 5=0.0101, обратный код -5=1.1010+1=1.1011

3=0.0011

0.0101 1.1101 0.0010

Одноразрядный сумматор

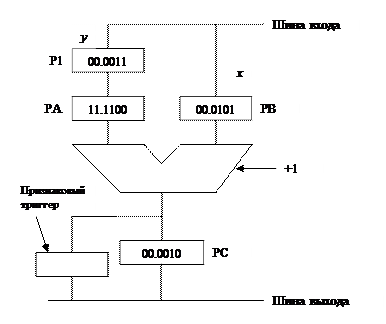
При выполнение операции вычитания x-y, уменьшаемое x подается на регистр РВ, вычитаемое e подается на регистр Р1; чтобы получить дополнительный код y информацию с Р1 на РА записывают в обратном коде, то есть инвертируется, снимается информация с инверсных выходов регистра Р1 при перезаписи.

В сумматоре складывается содержимое РА и РВ и +1 к младшему разряду.

Таким образом, в сумматоре к уменьшаемому x прибавляется дополнительный код вычитаемого y. На регистре РС фиксируется результат выполненной операции, который затем по шине выхода записывается в память. На признаковых триггерах фиксируется Т-признак - результат выполненной операции, то есть больше, меньше или равно нулю, или переполнение (формат чисел с фиксированной и плавающей точкой в обратном и дополнительном коде).

При выполнение операции сложения на регистры РВ и Р1 заносятся два слагаемых. На РА и Р1 передается без изменения. В АЛУ суммируются два числа РА и РВ, результат заносится на РС и Т-признак.

Пример

(-3) – (-5)

Микропрограмма операции вычитания

V₁ РВ=Ш_вх

V₂ Р1=Ш_вх

 

 

АЛУ для выполнения операции умножения над числами с фиксированной точкой, представленных в прямом коде

Существуют 4 основных подхода для выполнения операции умножения. 1 и 2 подходы связаны с анализом множителя, начиная с младших разрядов; 3 и 4 – анализ множителя, начиная со старших разрядов.

1 подход

Метод умножения, начиная с анализа младших разрядов множителя, со сдвигом множимого влево (метод похож на метод ручного умножения).

2 подход

Метод умножения, начиная с анализа младших разрядов множителя, со сдвигом суммы частичных произведений.

3 подход

Метод умножения, начиная с анализа старших разрядов множителя, со сдвигом множимого вправо.

4 подход

Метод умножения, начиная с анализа старших разрядов множителя, со сдвигом суммы частичных произведений влево.

Наиболее экономичным по аппаратуре является 2 метод, так как он требует n-разрядных регистров для представления множимого, множителя и суммы частичных произведений.

 

Структурная схема АЛУ для выполнения операции умножения над числами с фиксированной точкой, представленных в прямом коде (по 2 методу)

Швх

Р1- регистр множимого;

Р2 – регистр множителя;

РВ – регистр суммы частичных произведений (в начале выполняется операции умножения обнуляется);

СМ – выход сумматора (каждый цикл на нем фиксируется суммой частичных произведений до сдвига);

РС – регистр сумматора (на нем фиксируется сумма частичных произведений после сдвига и затем заносится на регистр РВ);

Р21 – предназначен для сдвига множителя вправо, чтобы каждый цикл можно было анализировать очередной младший разряд множителя.

Результат выполнения операции умножения имеет 2n разрядов. Старшая часть образуется Ра регистре РС, младшая часть образуется на регистре Р21.

Триггер знака предназначен для фиксирования знака выполняемой операции умножения путем выполнения операции сложения по модулю 2 знаковых разрядов операндов.

c=a(+)b

a	b	c

После этого знаковые разряды операндов обнуляются.

 

 

n=4 – длина разрядной сетки

(n-1) – число значащих разрядов

 

Швх

Ø Обратиться к теме «Микропрограммное УУ».

В зависимости от значения младшего триггера выполняется либо одна ветка, либо другая.

 

(*) _{результат}

0 0 1 1 0 0 1 0_{з сдвинуть вправо на 1 разряд}

РС Р21

0 0 0 1 1 0 0 1

РС Р21

 

Третий этап коррекции результата. Для этого на РА надо поставить нули, либо в счётчик заносить не (n-1), а n.

Этапы умножения.

Этап.

Определили знак результата. Знаковые разряды операндов складываются по модулю 2, и результат заносится в знаковый разряд. Знаковые разряды после этого обнуляются.

Этап.

В счётчик цикла заносится число (n-1) – число значащих разрядов, а n – длина разрядной сетки.

На втором этапе происходит обработка (n-1) циклов.

На каждом цикле анализируется очередной младший разряд множителя (регистр Р2). Если младший разряд равен 1, то переписываем на РА содержимое регистра Р1 (это переход на микропрограммный уровень); а если младший разряд равен 0, то обнуляем РА. После этого в сумматоре складывается содержимое РА и РВ (РВ предварительно обнулили), и на выходе сумматора СМ образуется сумма частичных произведений до сдвига. На РС заносится сумма частичных произведений после сдвига, которая потом переписывается на РВ. Младший разряд сумматора при сдвиге будет заноситься в старший разряд Р21, и он будет (освобождающийся) представлять собой младший разряд произведения. В этом же цикле множитель сдвигается на один разряд вправо путём пересылки с Р2 на Р21, и после записываем на Р2. Счётчик цикла уменьшаем на 1. Если счётчик цикла равен 0, то дальше идёт коррекция результата: старшая часть на РС, младшая на Р21, происходит сдвиг на один разряд. Либо сразу вместо коррекции можно взять n.