
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайная величина. Закон распределения вероятностей дискретной случайной величины. Формулы для вычисления основных числовых характеристик непрерывной случайной величины.
Случайная величина называется дискретной, если ее множество значений счетно. Любое пространство элементарных событий не являющееся дискретным, называется недискретным, и при этом, если наблюдаемыми результатами (нельзя произносить случайными событиями) являются точки того или иного числового арифметического или координатного пространства, то пространство называется непрерывным (континуум). Пространство элементарных событий вместе с алгеброй событий и вероятностью образует тройку, которая называется вероятностным пространством. Непрерывные случайные величины. Плотность вероятности. Случайная величина Для непрерывной случайной величины
а также
где F(x) функция распределения величины Пусть f(x) - неотрицательная интегрируемая функция, определенная на всей числовой оси и удовлетворяющая условию
Тогда функция
обладает всеми свойствами функции распределения. Кроме того, F(x) непрерывна в любой точке (и слева, и справа). Следовательно, случайная величина Мы говорим, что случайная величина Из определения плотности вероятности f(x) и свойств функции распределения следует, что f(x) должна удовлетворять условию (1). И обратно, если Если случайная величина
Числовые ряды. Основные понятия. Необходимый признак сходимости числового ряда Пусть положительные числа называется числовым рядом. Здесь Зная общий член ряда, можно записать ряд в форме (1). Так общим членом Рассмотрим для числового ряда (1) суммы его первых членов
Будем называть их частичными суммами и обозначим соответственно через Если для некоторого числового ряда бесконечная последовательность его частичных сумм имеет конечный предел, то этот ряд называется сходящимся. Этот предел Если последовательность частичных сумм ряда не имеет определенного предела, то ряд называется расходящимся и для него не существует суммы. Рассмотрим примеры на исследование сходимости ряда по определению. Пример 1. Дан ряд Это геометрическая прогрессия с первым членом Частичная сумма ряда 1) если Значит, в случае 2) если 3) если В этом случае 4) если В этом случае Следовательно, Таким образом, ряд Пример 2. Рассмотрим ряд который называется обобщенным гармоническим рядом. 1) пусть Составим n-ю частичную сумму По условию 2) при т.о. обобщенный гармонический ряд При Пример 3. Рассмотрим ряд Общий член заданного ряда может быть представлен в виде: Определим частичную сумму ряда Отсюда Для рассмотренных рядов операция суммирования оказалась сравнительно несложной. Вообще же этот прием, если он и выполним, связан со сложными вычислениями. Поэтому для исследования характера ряда применяют признаки сходимости. 2. Необходимый признак сходимости. Теорема. Если числовой ряд Доказательство. Пусть данный ряд сходится. Тогда по определению сходящегося ряда
так как вместе с Здесь Поэтому Отсюда
|
||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.136.170 (0.012 с.) |
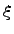 называется непрерывной, если ее функция распределения F(x) непрерывна на всей числовой оси.
называется непрерывной, если ее функция распределения F(x) непрерывна на всей числовой оси. имеет место равенство
имеет место равенство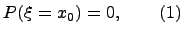



 имеет место равенство (2). При этом f(x) называется плотностью вероятности случайной величины
имеет место равенство (2). При этом f(x) называется плотностью вероятности случайной величины  и выполняется условие (1), то f(x) является плотностью вероятности.
и выполняется условие (1), то f(x) является плотностью вероятности.
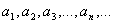 - члены некоторой бесконечной числовой последовательности. Тогда выражение вида
- члены некоторой бесконечной числовой последовательности. Тогда выражение вида (1)
(1)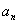 – общий член ряда, с помощью которого ряд (1) записывается в виде
– общий член ряда, с помощью которого ряд (1) записывается в виде
 задается числовой ряд
задается числовой ряд


 называется суммой ряда.
называется суммой ряда.
 и знаменателем
и знаменателем  .
. или
или  .
. , то
, то  , при
, при  и, следовательно,
и, следовательно,
 .
.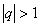 , то
, то  , при
, при  ,т.е.
,т.е.  не существует и ряд расходится
не существует и ряд расходится то данный ряд имеет вид
то данный ряд имеет вид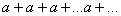
 , т.е. ряд расходится.
, т.е. ряд расходится. , то имеем ряд
, то имеем ряд

 предела не имеет и ряд расходится
предела не имеет и ряд расходится сходится только тогда, когда знаменатель прогрессии по абсолютной величине меньше единицы.
сходится только тогда, когда знаменатель прогрессии по абсолютной величине меньше единицы.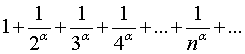 ,
,

 , т.о.
, т.о. , следовательно, ряд расходится
, следовательно, ряд расходится
 и ряд будет сходящимся.
и ряд будет сходящимся. расходится при
расходится при  получим ряд вида
получим ряд вида  , который называется гармоническим и является расходящимся рядом.
, который называется гармоническим и является расходящимся рядом.
 , сравнив числители дробей, получим значения
, сравнив числители дробей, получим значения  ,
,  и, таким образом,
и, таким образом, 

 , и, таким образом, заданный ряд сходится.
, и, таким образом, заданный ряд сходится.
 ;
; , то
, то  , т.е.
, т.е.
 , а
, а  .
.
 , что и требовалось доказать.
, что и требовалось доказать.


