Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства операций над отношениями
Приведем здесь список основных свойств операций над отношениями и докажем некоторые из них. 1) 3) (R1 o R2) –1 = R1 –1o R2 –1. 4) (R1 o R2 ) o R3 = R1 o (R2 o R3). 5) (R1 È R2 ) o R3 = (R1 o R3 ) È (R2 o R3 ). 6) (R1 Ç R2 ) o R3 Í (R1 o R3 ) Ç (R2 o R3 ). 7) а) если R1 Í R2 то R1 o R3 Í R2 o R3; б) если R1 Í R2 то R3 o R1 Í R3 o R2; в) если R1 Í R2 то R1–1Í R2–1. 8) a) (R1È R2)d = R1d Ç R2d; б) (R1Ç R2)d = R1d È R2d; в) (Rd)d = R. Доказательства Свойство 2. Пусть пара (x, y)Î(È Rk) –1. Тогда (y, x)ÎÈ Rk. Это означает, что найдется отношение Rj, что (y, x)Î Rj. Отсюда, по определению обратного отношения, (x, y)ÎRj–1, а значит, (x, y)ÎÈRk–1и (ÈRk)–1 Í È Rk–1. Докажем обратное включение. Пусть (x,y)Î Rk–1 Это означает, что найдется такое множество Rj, что (x,y)ÎRj–1. Следовательно, (y, x)ÎRj и (y, x)Î ÈRk, поэтому (x, y)Î(È Rk)–1. Значит, È Rk–1 Í (ÈRk)–1. Одновременное выполнение обоих включений означает равенство множеств, что и требовалось доказать. Свойство 6. Пусть (x, y)Î(R1 Ç R2) o R3. По определению композиции это означает, что найдется такое zÎA, что (x, z)Î(R1 Ç R2) и (z, y)ÎR3. Первое включение возможно только тогда, когда одновременно выполнено (x, z)ÎR1 и (x, z)ÎR2. Это, в свою очередь, означает, с учетом (z, y)ÎR3, что одновременно (x, y)Î R1 o R3 и (x, y)ÎR2 o R3, а, следовательно, (x, y)Î(R1 o R3) Ç (R2 o R3), что и доказывает требуемое соотношение. Замечание. Покажем, почему неверно обратное включение. Пусть (x, y) Î(R1 o R3) Ç (R2 o R3), тогда (x, y) Î(R1 o R3) и (x, y) Î(R2 o R3). Первое включение означает существование такого элемента z1 из A, что (x, z1)ÎR1 и (z1, y) ÎR3; второе – существование такого z2ÎA, что (x, z2)ÎR2 и (z2, y)ÎR3, причем необязательно z1 = z2. Значит, не всегда существует такой элемент z, что (x, z)ÎR1 и (x, z)ÎR2, а, следовательно, не будет принадлежности пересечению R1 и R2. Свойство 7в. Возьмём любую пару (x, y)ÎR1, что эквивалентно (y, х)ÎR1–1. Пусть теперь R1 Í R2, т.е. из (x, y)ÎR1 следует (x, y)ÎR2. Перейдя к обратным отношениям, получим, что из (y, х)ÎR1–1 вытекает (y, х)ÎR2–1, что и означает требуемое свойство. Свойство 8а). Докажем предварительно равенство Пусть (x, y)Î
Для доказательства свойства 8а) воспользуемся доказанным равенством и известными свойствами операций над множествами и отношениями.
(R1 È R2)d = = (`R1 Ç`R2)–1 =`R1–1 Ç R2–1 = R1d Ç R2d. 3. Способы задания отношений Традиционное задание отношений аналогично тому, как это принято в теории множеств, что не всегда удобно. Поэтому, наряду с таким заданием, применяются другие способы. 1. Матричное задание. Оно используется когда А – конечное или счетное множество А = {xi}. Тогда бинарное отношение R можно задавать с помощью матрицы R = {xij}, элементы которой определяются соотношением:
2. Табличное задание. Этим способом можно задавать произвольное n-арное отношение. Он используется, когда Аi – конечные или счетные множества Аi = {xij}. Строки таблицы соответствуют различным n-мерным элементам отношения, столбцы – наборам элементов из множеств Аi. 3. Задание с помощью графа. Для конечного или счетного множества А бинарное отношение можно задавать с помощью графа Г(R), который является геометрическим образом бинарного отношения. Граф – фигура состоящая из точек (вершин) соединенных линиями (дугами). Вершины графа соответствуют элементам множества А, то есть xi, а наличие дуги, соединяющей вершины xi и xj, означает, что (xi, xj)ÎR. Чтобы подчеркнуть упорядоченность пары на дуге ставится стрелка. Основные свойства графа. 1) Г(R–1) получается из Г(R) изменением направления стрелок на противоположные. 2) Граф Г(А´А) содержит дуги, соединяющие любую пару (xi, xj). Такой граф называется полным. 4. Задание верхними и нижними срезами. Этот способ может быть использован для любых множеств и бинарных отношений. Пусть на множестве А задано отношение R. Верхний срез GR(x) отношения R в точке x ÎА – это множество элементов yÎА таких, что (y, x)ÎR, т.е. GR(x) = { yÎA | (y, x)ÎR }. Если рассматривать R как отношение предпочтения, то GR (x) – это множество элементов, лучших, чем х. Нижний срез HR(x) отношения R в точке xÎА – это множество элементов yÎА, таких, что (x, y)ÎR, т.е. HR(x) = { yÎA | (x, y)ÎR }. Свойства нижних и верхних срезов. Для любого хÎA и любого отношения Ri Í A´A выполняются соотношения.
1. а) GRÇR(x) = GR(x) Ç GR(x); б) HRÇR(x) = HR(x) Ç HR(x) 2. a) G`R(x) = A \ GR(x); б) H`R(x) = A \ HR(x). 3. a) GR–1(x) = HR(x); б) HR–1(x) = HR(x). 4. GA´A(x) = HA´A(x) = A.
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.186.223 (0.012 с.) |
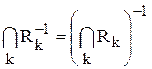 2)
2) 
 =
=  .
. , то (x, y) ÏR–1 и (y, x)ÏR. Тогда (y, x)Î`R или, что то же самое, (x,y)Î(`R)–1.
, то (x, y) ÏR–1 и (y, x)ÏR. Тогда (y, x)Î`R или, что то же самое, (x,y)Î(`R)–1.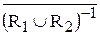 =
=  =
=