Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами
Розглянемо лінійне неоднорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами
Відповідно до теореми (8.5) загальний розв'язок такого рівняння дорівнює сумі загального розв'язку відповідного йому однорідного рівняння і якого-небудь частинного розв'язку неоднорідного рівняння. Оскільки відповідне однорідне рівняння завжди розв’язується, то нам залишається лише знайти який-небудь частинний розв'язок даного рівняння. Для довільної функції Але для досить широкого класу функцій Метод застосовується для функцій вигляду
де
Дана функція містить у собі декілька більш простих частинних випадків. Наприклад: при при при при при Метод заснований на тому, що частинний розв'язок рівняння (8.34) має вигляд правої частини рівняння. Теорема 8.6. Якщо число
де Якщо ж число
Якщо ж число
Доведемо цю теорему для випадку, коли Нехай частинний розв'язок рівняння
має вигляд
Підставимо
Вираз (8.39) є рівністю двох многочленів. Підібрати коефіцієнти многочлена
Якщо ж Якщо ж Аналогічно можна довести справедливість теореми (8.6) для інших окремих випадків функції Приклад 8.14. Знайти загальний розв'язок рівняння
Розв’язання. Загальний розв'язок рівняння має вигляд Однорідне рівняння, що відповідає даному, має вигляд
Його характеристичне рівняння Функція правої частини рівняння
Підберемо коефіцієнти
Підставимо
Порівнюючи коефіцієнти при x і вільні члени лівої і правої частин рівняння, отримаємо систему:
Звідки Отже, частинний розв'язок даного рівняння має вигляд
Приклад 8.15. Знайти частинний розв'язок рівняння Розв’язання. Однорідне рівняння, що відповідає заданому, має вигляд Підберемо коефіцієнти так, щоб функція задовольняла рівняння. Обчислимо похідні частинного розв'язку і підставимо їх у задане рівняння
Тоді Прирівняємо коефіцієнти при однакових функціях у лівій та правій частині рівності:
Розв’язуючи систему цих рівнянь, знаходимо, що,
Загальний розв'язок рівняння буде
Похідна загального розв'язку запишеться так
Підставимо в загальний розв'язок та його похідну початкові умови при Одержимо систему рівнянь
Звідки Частинний розв'язок рівняння, що задовольняє зазначені початкові умови, має вигляд
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.198.36 (0.024 с.) |
 . (8.34)
. (8.34) це робиться за методом варіації довільних сталих і частинний розв'язок має вигляд (8.33).
це робиться за методом варіації довільних сталих і частинний розв'язок має вигляд (8.33). ,
,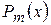 і
і  – многочлени відповідно порядків
– многочлени відповідно порядків  і
і 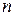 :
: ;
;
 функція приймає вигляд
функція приймає вигляд  ;
; –
–  ;
;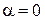 –
–  ;
;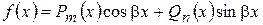 ;
; ,
,  –
–  .
. , складене за правою частиною рівняння (
, складене за правою частиною рівняння ( – коефіцієнт показника показникової функції,
– коефіцієнт показника показникової функції, 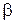 – коефіцієнт аргументу тригонометричної функції) не є коренем характеристичного рівняння, то частинний розв'язок рівняння (8.34) має вигляд
– коефіцієнт аргументу тригонометричної функції) не є коренем характеристичного рівняння, то частинний розв'язок рівняння (8.34) має вигляд , (8.35)
, (8.35)
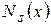 – многочлени з невизначеними коефіцієнтами порядку
– многочлени з невизначеними коефіцієнтами порядку  .
. . (8.36)
. (8.36) . (8.37)
. (8.37) . Для такої функції
. Для такої функції 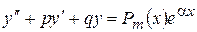 (8.38)
(8.38)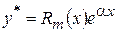 , де
, де  – многочлен з невизначеними коефіцієнтами порядку
– многочлен з невизначеними коефіцієнтами порядку 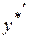 ,
, 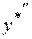 :
: ;
; .
.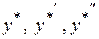 в рівняння (8.38) і поділимо всі його члени на функцію
в рівняння (8.38) і поділимо всі його члени на функцію  , яка ні при яких значеннях аргументу x не перетворюється на нуль. Групуючи доданки за
, яка ні при яких значеннях аргументу x не перетворюється на нуль. Групуючи доданки за 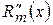 ,
, 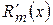 ,
,  . (8.39)
. (8.39)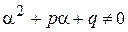 , що свідчить про те, що
, що свідчить про те, що 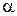 не корінь характеристичного рівняння
не корінь характеристичного рівняння 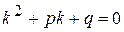 .
.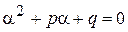 , а
, а 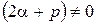 (число
(число  .
. , тобто
, тобто 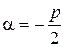 (число
(число 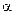 є коренем характеристичного рівняння два рази), рівність (8.38) буде правильною, якщо підставити в рівняння (8.38) такий многочлен, що після диференціювання двічі перетворився б у многочлен порядку
є коренем характеристичного рівняння два рази), рівність (8.38) буде правильною, якщо підставити в рівняння (8.38) такий многочлен, що після диференціювання двічі перетворився б у многочлен порядку 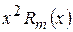 . Значення коефіцієнтів многочлена
. Значення коефіцієнтів многочлена 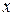 лівої і правої частини рівності (8.39).
лівої і правої частини рівності (8.39).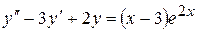 .
. , де
, де 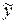 – загальний розв'язок рівняння однорідного, відповідного даному,
– загальний розв'язок рівняння однорідного, відповідного даному, 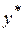 – частинний розв'язок даного рівняння.
– частинний розв'язок даного рівняння. .
. має корені
має корені  ,
,  (дійсні і різні), тому загальний розв'язок однорідного рівняння
(дійсні і різні), тому загальний розв'язок однорідного рівняння  .
. – добуток многочлена першого порядку на показникову функцію. Тоді
– добуток многочлена першого порядку на показникову функцію. Тоді
 і
і  так, щоб
так, щоб 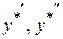 :
: ;
;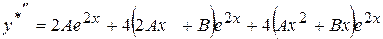 .
.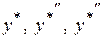 в диференціальне рівняння, поділимо його члени на
в диференціальне рівняння, поділимо його члени на 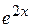 і спростимо, тоді одержимо:
і спростимо, тоді одержимо: .
.

 , а його загальний розв'язок
, а його загальний розв'язок
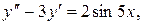 якщо
якщо 
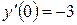 .
. . Його характеристичне рівняння
. Його характеристичне рівняння  має корені
має корені 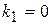 ,
,  (дійсні і різні), тому
(дійсні і різні), тому  Функція правої частини рівняння
Функція правої частини рівняння 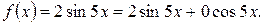 Для неї число
Для неї число  . Серед коренів характеристичного рівняння числа
. Серед коренів характеристичного рівняння числа  немає, тому частинний розв'язок рівняння має вигляд правої частини:
немає, тому частинний розв'язок рівняння має вигляд правої частини:  .
. ;
; 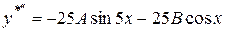 .
. .
.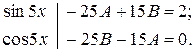

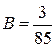 . Частинний розв'язок рівняння має вигляд
. Частинний розв'язок рівняння має вигляд .
.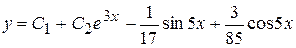 .
. .
. ,
, 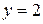 ,
,  .
.
 ,
,  .
. .
.