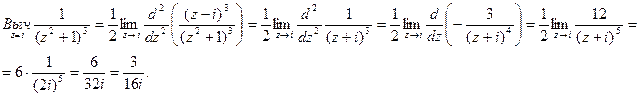Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Можно доказать, что предел суммы, стоящий в правой части равенства равен интегралу
Тогда
- представление функции f(x) интегралом Фурье.
Двойной интеграл Фурье для функции f(x) можно представить в комплексной форме:
Преобразование Фурье.
Определение. Если f(x) – любая абсолютно интегрируемая на всей числовой оси функция, непрерывная или имеющая конечное число точек разрыва первого рода на каждом отрезке, то функция
называется преобразованием Фурье функции f(x). Функция F(u) называется также спектральной характеристикой функции f(x).
Если f(x) – функция, представимая интегралом Фурье, то можно записать:
Это равенство называется обратным преобразованием Фурье
Интегралы
Косинус – преобразование Фурье будет преобразованием Фурье для четных функций, синус – преобразование – для нечетных. Преобразование Фурье применяется в функциональном анализе, гармоническом анализе, операционном исчислении, теории линейных систем и др.
Элементы теории функций комплексного переменного.
Определение. Если каждому комплексному числу z из некоторого множества D по некоторому закону поставлено в соответствие определенное комплексное число w из множества G, то на этой области задана однозначная функция комплексного переменного, отображающая множество D на множество G. w = f(z) Множество D называется областью определения, множество G – областью значений функции.
Комплексную функцию можно записать в виде:
u, v – действительные функции от переменных х и у.
Если каждому z Î D соответствует несколько различных значений w, то функция w=f(z) называется многозначной.
Определение. Функция
Свойства функций комплексного переменного.
Для функций комплексного переменного f(z) и g(z) справедливы следующие свойства:
1) 2) 3)
Определение. Функция
Основные трансцендентные функции.
Определение. Трансцендентными называются аналитические функции, которые не являются алгебраическими.
Если аргументом показательной или тригонометрических функций является комплексное число, то определение этих функций, вводимое в элементарной алгебре теряет смысл.
Рассмотрим разложение в степенной ряд следующих функций:
См. Представление функций по формуле Тейлора.
Функции ez, cosz, sinz связаны между собой формулой Эйлера (см. Уравнение Эйлера.) Эта формула может быть очень легко получена сложением соотвествующих рядов.
Также справедливы равенства:
Для тригонометрических функций комплексного аргумента справедливы основные тригонометрические тождества (синус и косинус суммы, разности и т.д.), которые справедливы для функций действительного аргумента.
Определение. Гиперболическим синусом, косинусом, тангенсом и котангенсом называются соответственно функции:
Гиперболические функции могут быть выражены через тригонометрические:
Гиперболические функции sh z и ch z имеют период 2pi, а функции th z и cth z – период pi.
Пример. Найти sin(1+2i).
Определение. Логарифмическая функция комплексного аргумента определяется как функция, обратная показательной.
Если w = u + iv, то Тогда eu =
Итого:
Для комплексного числа z = a + ib
Определение. Выражение
Логарифмическая функция комплексного аргумента обладает следующими свойствами: 1) 2) 3) 4)
Обратные тригонометрические функции комплексного переменного имеют вид:
Производная функций комплексного переменного.
Определение. Производной от однозначной функции w = f(z) в точке z называется предел:
Определение. Функция f(z), имеющая непрерывную производную в любой точке области D называется аналитической функцией на этой области.
Правила дифференцирования функций комплексного аргумента не отличаются от правил дифференцирования функций действительной переменной. Аналогично определяются производные основных функций таких как синус, косинус, тангенс и котангенс, степенная функция и т.д. Производные гиперболических функций определяются по формулам:
Вывод правил интегрирования, значений производных основных функций ничем не отличается от аналогичных операций с функциями действительного аргумента, поэтому подробно рассматривать их не будем.
Условия Коши – Римана. (Бернхард Риман (1826 – 1866) – немецкий математик)
Рассмотрим функцию комплексной переменной
Стремление к нулю Dz®0 может осуществляться в следующих случаях:
1) 2)
В первом случае:
Во втором случае:
Тогда должны выполняться равенства:
Эти равенства называются условиями Коши – Римана, хотя еще раньше они были получены Эйлером и Даламбером.
Теорема. Если функция z = x + iy, то ее действительные компоненты u и v имеют в точке (х, у) частные производные первого порядка, удовлетворяющие условию Коши – Римана.
Также справедлива и обратная теорема. На основании этих теорем можно сделать вывод, что из существования производной следует непрерывность функции.
Теорема. Для того, чтобы функция
Интегрирование функций комплексной переменной.
Пусть
В L
А х
Кривая L задана уравнением
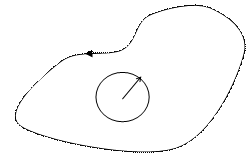
Определение. Интеграл от функции f(z) вдоль кривой L определяется следующим образом:
Если учесть, что
Теорема. (Теорема Коши) Если f(z) - аналитическая функция на некоторой области, то интеграл от f(z) по любому кусочно – гладкому контуру, принадлежащему этой области равен нулю.
Интегральная формула Коши.
Если функция f(z) – аналитическая в односвязной замкнутой области с кусочно – гладкой границей L.
D
r z0
Тогда справедлива формула Коши:
где z0 – любая точка внутри контура L, интегрирование по контуру производится в положительном направлении (против часовой стрелки).
Эта формула также называется интегралом Коши.
Ряды Тейлора и Лорана. (Пьер Альфонс Лоран (1813 – 1854) – французский математик)
Функция f(z), аналитическая в круге
Коэффициенты ряда вычисляются по формулам:
Степенной ряд с коэффициентами такого вида называется рядом Тейлора.
Рассмотрим теперь функцию f(z), аналитическую в кольце
Ряд такого вида называется рядом Лорана. При этом функция f(z) может быть представлена в виде суммы:
Ряд, определяющий функцию f1( x), называется правильной частью ряда Лорана, а ряд, определяющий функцию f2(x), называется главной частью ряда Лорана.
Если предположить, что r = 0, то можно считать, что функция аналитична в открытом круге
Тогда точка z0 называется изолированной особой точкой функции f.
Рассмотрим следующие частные случаи:
1) Функция f(x) имеет вид: В этом случае говорят, что особенность функции f в точке z0 устранима. Для устранения особой точки достаточно доопределить функцию в центре круга (f(z0) = c0) и функция будет аналитической не только в окрестности центра круга, но и в самом центре. В этом случае
2) Функция f(x) имеет вид: В этом случае точка z0 называется полюсом функции f(z) порядка (кратности) m. При m = 1 точку z0 называют еще простым полюсом. Порядок полюса может быть определен по формуле:
z0 – полюс порядка т. 3) Функция f(z) имеет вид В этом случае говорят, что функция f(z) имеет в точке z0 существенно особую точку.
Определение. Пусть z0 – изолированная особая точка функция f(z), т.е. пусть функция f(z) – аналитическая в некотором круге
называется вычетом функции f(z) в точке z0, где L – контур в круге
Вычет также обозначают иногда
Если Таким образом, если известно разложение функции в ряд Лорана, то вычет легко может быть найден в случае любой особой точки.
В частных случаях вычет может быть найден и без разложения в ряд Лорана.
Например, если функция
Тогда можно показать, что вычет находится по формуле
Пример. Найти вычет функции
Эта точка является полюсом второго порядка. Получаем:
Теорема о вычетах.
Теорема. Пусть функция f(z) – аналитическая на всей плоскости z, за исключением конечного числа точек z1, z2, …, zN. Тогда верно равенство:
А интеграл от функции по контуру L, содержащему внутри себя эти точки, равен
Эти свойства применяются для вычисления интегралов. Если функция f(z) аналитическая в верхней полуплоскости, включая действительную ось, за исключением N точек, то справедлива формула
Пример. Вычислить определенный интеграл
Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки 2i. Эта точка является полюсом второго порядка. Найдем вычет функции
Получаем
Пример. Вычислить определенный интеграл
Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки i. Эта точка является полюсом второго порядка. Найдем вычет функции
Получаем
|
||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 307; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.169.223 (0.135 с.) |


 Окончательно получаем:
Окончательно получаем:

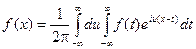
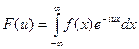

 и
и  называются соответственно косинус - преобразование Фурье и синус – преобразование Фурье.
называются соответственно косинус - преобразование Фурье и синус – преобразование Фурье.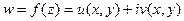


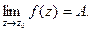




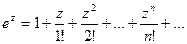




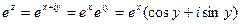




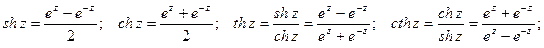


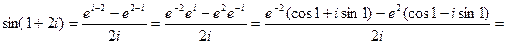


 и Arg ew =
и Arg ew = 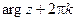 = v.
= v.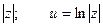 .
.

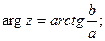
 называется главным значением логарифма.
называется главным значением логарифма.

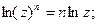
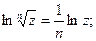
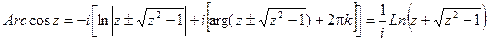







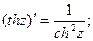
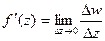








 у
у

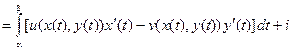

 , то
, то



 , разлагается в сходящийся к ней степенной ряд по степеням (z – z0).
, разлагается в сходящийся к ней степенной ряд по степеням (z – z0).

 . Эта функция может быть представлена в виде сходящегося ряда:
. Эта функция может быть представлена в виде сходящегося ряда:
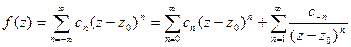

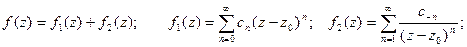
 за исключением центральной точки z0. Как правило, в этой точке функция бывает не определена.
за исключением центральной точки z0. Как правило, в этой точке функция бывает не определена. . Т.к. степенной ряд сходится во всех точках внутри круга, то его сумма f1(x) определена и непрерывно дифференцируема во всех точках круга, а, следовательно, и в центре круга z0.
. Т.к. степенной ряд сходится во всех точках внутри круга, то его сумма f1(x) определена и непрерывно дифференцируема во всех точках круга, а, следовательно, и в центре круга z0. .
.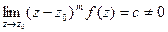
 , где в ряду
, где в ряду 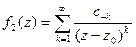 не равно нулю бесконечное количество коэффициентов с-k.
не равно нулю бесконечное количество коэффициентов с-k.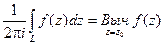
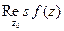 .
. есть ряд Лорана функции f в точке z0, то
есть ряд Лорана функции f в точке z0, то 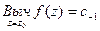 .
.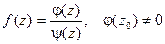 , а
, а  имеет простой нуль при z = z0
имеет простой нуль при z = z0 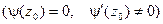 , то z = z0 является простым полюсом функции f(z).
, то z = z0 является простым полюсом функции f(z).
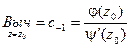
 Если z = z0 – полюс порядка m ³ 1, то вычет может быть найден по формуле:
Если z = z0 – полюс порядка m ³ 1, то вычет может быть найден по формуле: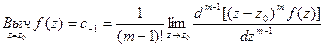
 относительно точки z = 2.
относительно точки z = 2.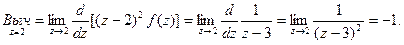




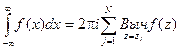
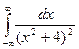 .
.