
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценки параметров генеральной совокупности ⇐ ПредыдущаяСтр 8 из 8
ПО ЕЕ ВЫБОРКЕ Пусть в эксперименте изучается случайная величина X и, из теоретических соображений, известен ее закон распределения. Естественно, возникает задача оценки (приближенного нахождения) параметров Обычно в распоряжении исследователя имеются лишь данные выборки генеральной совокупности, например ( 1. Числовые характеристики выборки. Выборочной средней
Если же значения выборки
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения Выборочной дисперсией Если все значения
Если же значения признака
Можно показать, что
Выборочным средним квадратическим отклонением
Особенность
Пример. Выборочным путем были получены следующие данные о массе 20 хомячков при рождении (в г): 30, 30, 25, 32, 30, 25, 33, 32, 29, 28, 27, 36, 31, 34, 30, 23, 28, 34, 36, 30. Найти выборочную среднюю Согласно формулам имеем:
2. Оценки параметров распределения. Для оценки параметров распределения
Несмещенной называют оценку
в противном случае оценка называется смещенной. Пример 1. Оценка Пример 2. Оценка
Естественно в качестве приближенного неизвестного параметра брать несмещенные оценки, для того чтобы не делать систематической ошибки в сторону завышения или занижения. Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия:
Для оценки генерального среднего квадратического отклонения используют исправленное среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:
3. Метод моментов. Пусть изучается случайная величина X с математическим ожиданием Точечной называют оценку, которая определяется одним числом. То есть точечная оценка характеристики генеральной совокупности — это число, определяемое по выборке. Метод моментов для нахождения точечных оценок неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов распределения соответствующим эмпирическим моментам, найденных по выборке. Так, если распределение зависит от одного параметра
Если распределение зависит от двух параметров, то надо решить относительно
Пример. Пусть СВ Х имеет распределение Пуассона: Решение. Известно, что математическое ожидание распределения Пуассона
4. Доверительные интервалы. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал
При этом интервал Величина Для оценки математического ожидания
где
Для оценки математического ожидания
где
Метод наименьших квадратов для линейной зависимости
Предположим, что произведен эксперимент, в результате которого зафиксировано
Пусть вид зависимости линейный: tD b250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAA AAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEAjW80YYwHAACCOwAADgAAAAAAAAAAAAAA AAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAX2Eisd8AAAAKAQAADwAAAAAAAAAA AAAAAADmCQAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAPIKAAAAAA== ">
Построим функцию
Пусть параметры
Решая эту систему, находим параметры
Последовательность действий для определения вида зависимости 1) Результаты прямых измерений 2) Вычисляем средние значения:
3) Вычисляем дисперсии: 4) Находим оценки параметров: 5) Степень зависимости между а) если между переменными б) если между переменными в) при отсутствии линейной зависимости между переменными Итак, чем ближе по модулю коэффициент корреляции к нулю, тем слабее зависимость Встроенная линейная регрессия имеется, например, в программируемых калькуляторах и офисных программах (EXCEL). Пример. Найти уравнение прямой регрессии по четырем парам наблюдаемых значений (
Решение. Вычислим:
Следовательно, уравнение регрессии имеет вид: Вычислим коэффициент корреляции:
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 817; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.250.157 (0.034 с.) |
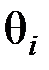 , которыми определяется это распределение. Например, если известно, что случайная величина
, которыми определяется это распределение. Например, если известно, что случайная величина  распределена в генеральной совокупности нормально, то необходимо оценить, т. е. приближенно найти математическое ожидание
распределена в генеральной совокупности нормально, то необходимо оценить, т. е. приближенно найти математическое ожидание  и среднее квадратическое отклонение
и среднее квадратическое отклонение  , так как эти два параметра полностью определяют нормальное распределение.
, так как эти два параметра полностью определяют нормальное распределение. ), полученные в результате п наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр.
), полученные в результате п наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр.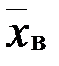 называется среднее арифметическое всех значений выборки. Если все значения
называется среднее арифметическое всех значений выборки. Если все значения  выборки объема п различны, то
выборки объема п различны, то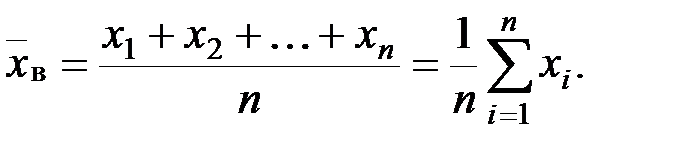
 имеют соответственно частоты
имеют соответственно частоты 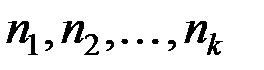 , причем
, причем  :
: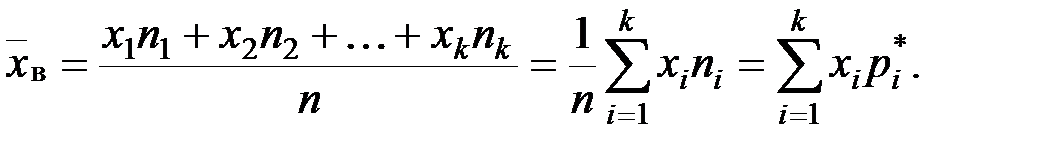
 , вводят выборочную дисперсию.
, вводят выборочную дисперсию. называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней
называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней  .
.


 называется квадратный корень из выборочной дисперсии:
называется квадратный корень из выборочной дисперсии: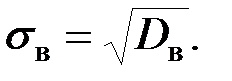
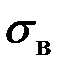 состоит в том, что оно измеряется в тех же единицах, что и измеряемый признак.
состоит в том, что оно измеряется в тех же единицах, что и измеряемый признак. .
.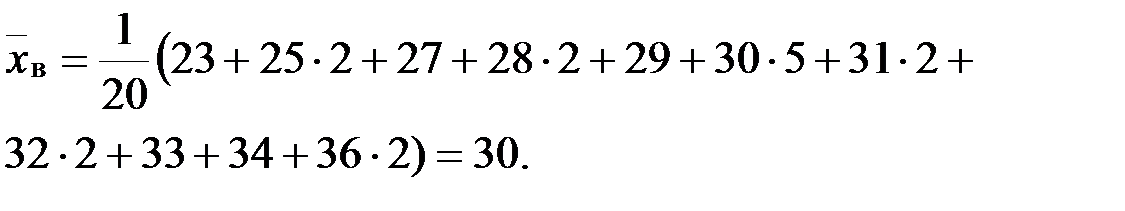

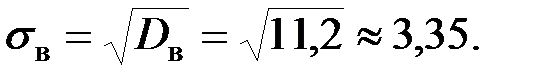
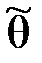 давала хорошее приближение, она должна удовлетворять определенным требованиям: быть несмещенной и состоятельной.
давала хорошее приближение, она должна удовлетворять определенным требованиям: быть несмещенной и состоятельной. :
:
 является несмещенной оценкой генеральной средней (математического ожидания), так как
является несмещенной оценкой генеральной средней (математического ожидания), так как 
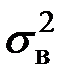 является смещенной оценкой генеральной дисперсии
является смещенной оценкой генеральной дисперсии  ,так как
,так как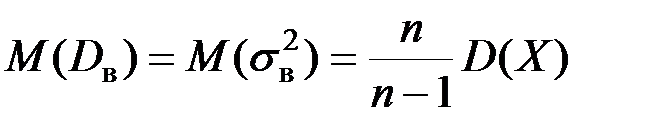 .
.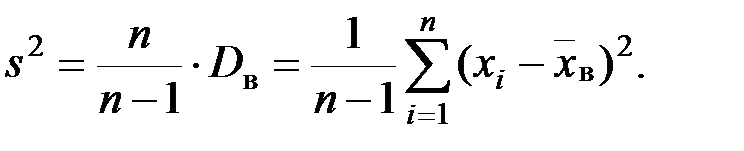

 и дисперсией
и дисперсией  и оба эти параметра неизвестны.
и оба эти параметра неизвестны.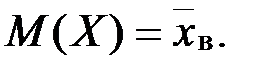
 и
и  систему уравнений
систему уравнений
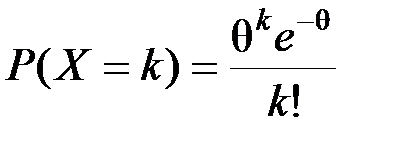 . Наблюдаемые:
. Наблюдаемые:  Нужно оценить неизвестный параметр
Нужно оценить неизвестный параметр  . Для того, чтобы найти оценку неизвестного параметра
. Для того, чтобы найти оценку неизвестного параметра  . Тогда оценка
. Тогда оценка 
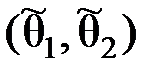 , относительно которого с заранее выбранной вероятностью
, относительно которого с заранее выбранной вероятностью  можно сказать, что внутри этого интервала находится точное значение оцениваемого параметра
можно сказать, что внутри этого интервала находится точное значение оцениваемого параметра .
. - уровнем значимости.
- уровнем значимости. .
. нормально распределенной случайной величины
нормально распределенной случайной величины  по выборочной средней
по выборочной средней  генеральной совокупности служит доверительный интервал
генеральной совокупности служит доверительный интервал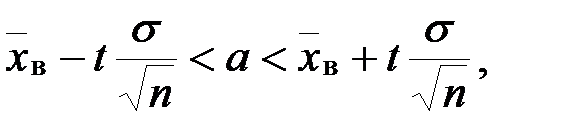
 - точность оценки;
- точность оценки; 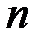 - объем выборки;
- объем выборки;  - такое значение аргумента функции Лапласа
- такое значение аргумента функции Лапласа  (см. Приложение), при котором
(см. Приложение), при котором  . То есть
. То есть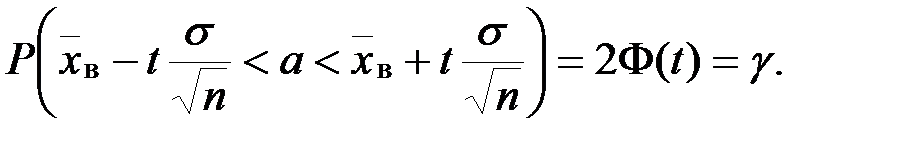

 - коэффициент Стьюдента, который находят по таблице по заданным
- коэффициент Стьюдента, который находят по таблице по заданным 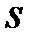 - исправленное среднее квадратическое отклонение.
- исправленное среднее квадратическое отклонение.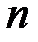 значений исследуемых переменных
значений исследуемых переменных  и
и  :
: 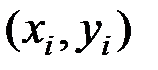
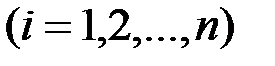 . Нанесем экспериментальные данные в виде точек в декартовой системе координат.
. Нанесем экспериментальные данные в виде точек в декартовой системе координат.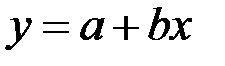 . Следующая задача экспериментатора – нахождение коэффициентов (параметров)
. Следующая задача экспериментатора – нахождение коэффициентов (параметров)  и
и 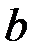 линейной эмпирической функции регрессии
линейной эмпирической функции регрессии  на
на  . Найдем эти коэффициенты методом наименьших квадратов.
. Найдем эти коэффициенты методом наименьших квадратов.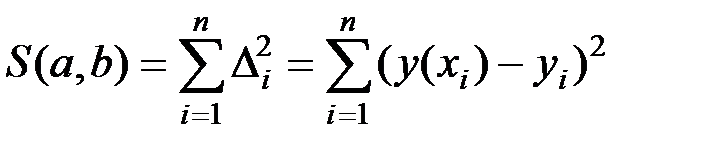 , равную сумме квадратов отклонений
, равную сумме квадратов отклонений  экспериментальных точек от искомой прямой
экспериментальных точек от искомой прямой  .
.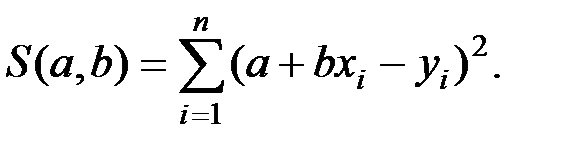
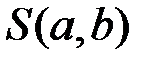 примет минимальное значение. Для этого приравняем частные производные функции
примет минимальное значение. Для этого приравняем частные производные функции 
 и
и  записываем в таблицу.
записываем в таблицу.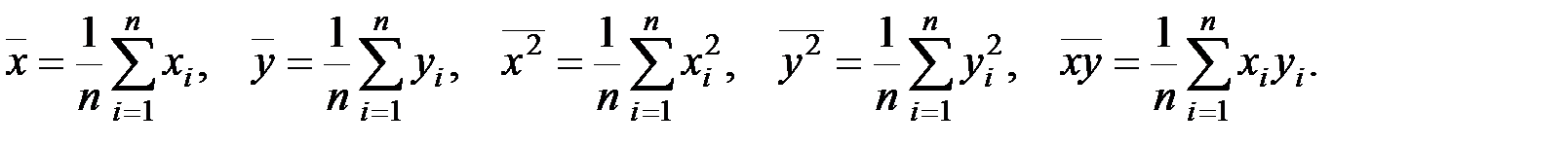
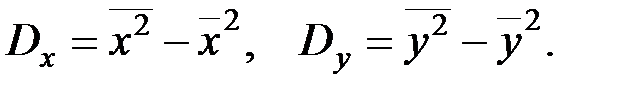

 При этом:
При этом: ;
; ;
; .
.


 .
. Результат близок к единице, следовательно между переменными
Результат близок к единице, следовательно между переменными 


