Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование релейно-контактных схемСодержание книги Поиск на нашем сайте Рассмотрим следующую задачу. Жюри состоит из трех членов А, B, C. Председателем жюри является А. После выполнения упражнения большинством голосов выносится вердикт – «зачтено» или «не зачтено». Учитывается, что в случае, когда B и C голосуют «за», а председатель голосует «против», то предложение «за» отвергается. Перед каждым членом жюри имеется кнопка, при нажатии которой его голос интерпретируется как «за». Лампочка загорается, если принято решение «за». Требуется соединить провода, источник питания, ключи (кнопки) и лампочку для автоматизации процесса голосования. Для решения задачи предварительно составим логическую функцию, считая ее функцией трех логических переменных
Рассмотрим три простейшие схемы (рис. 1.1 – 1.3), в которых стандартное положение ключа (кнопки) – открытое, при замыкании обеспечивается проводимость участка цепи. Для решения поставленной задачи достаточно несколько усложнить схему (рис. 1.4).
Рис. 1.1. Схема, реализующая «да» и «нет»
Рис. 1.2. Схема, реализующая конъюнкцию
Рис. 1.3. Схема, реализующая дизъюнкцию
Рис. 1.4. Схема, реализующая функцию
Схема, изображенная на рис. 1.4, и дает решение задачи. Однако с помощью конъюнкции и дизъюнкции невозможно построить произвольную логическую функцию, поскольку набор функций ( Электрические схемы, содержащие реле, называются релейно-контактными. С их помощью можно технически реализовать любую булеву функцию. Недостатком реле является сравнительно низкое быстродействие. Поэтому исторически роль реле перешла сначала к электронной лампе – триоду, далее к транзисторам, а затем к интегральным схемам с очень большой скоростью замыкания контактов ключей. Таким образом, логика работы релейно-контактных схем обеспечивается элементами, реализующими операции «И» (конъюнкция), «ИЛИ» (дизъюнкция) и «НЕ» (отрицание). Для построения оптимальной по количеству используемых ключей релейно-контактной схемы следует применить минимизацию. Метод Квайна – Мак-Класки позволяет привести СНДФ к минимальной НДФ. Однако следует иметь в виду, что если отказаться от требования нормальности, то полученную минимальную НДФ в большинстве случаев можно минимизировать далее. Пример. Дана функция в НДФ: Эту функцию можно записать в виде матрицы Функции соответствует релейно-контактная схема, содержащая два плеча, соединенных параллельно; в одном плече последовательно соединены ключи для реализации A, רB и C, во втором – Дальнейшую минимизацию можно осуществить путем вынесения общего множителя:
Рис. 1.5. Релейно-контактная схема Котрольное задание Варианты заданий по данной теме приведены в подразд. 1.3. Требуется выполнить следующее: – нарисовать релейно-контактную схему, соответствующую заданной СНДФ; – методом Квайна – Мак-Класки привести СНДФ к виду минимальной НДФ; – произвести (если это возможно) дальнейшую минимизацию, используя вынесение общих множителей за скобки; – нарисовать релейно-контактную схему для полученной логической функции. Моделирование сумматоров С помощью релейно-контактных схем можно построить модель арифметического сложения двоичных чисел. Для этого предварительно воспроизведем операцию сложения двух одноразрядных чисел. Требуется сопоставить с каждым из чисел, принимающих значения 0 и 1, высказывания «участок цепи разомкнут» и «участок цепи замкнут». В табл. 1.2 приведено сложение одноразрядных чисел.
Таблица 1.2 Сложение одноразрядных чисел
Высказываниям соответствует истинность или ложность логических аргументов
Рис. 1.6. Полусумматор на два входа
По этим таблицам истинности строим СНДФ функций
Используя полученные логические формулы, конструируем соответствующие релейно-контактные схемы. Упрощенно их можно представить в виде схемы (рис. 1.7), которая содержит инверторы (реализующие отрицание), дизъюнкторы (параллельное соединение) и конъюнкторы (последовательное соединение).
Рис. 1.7. Структурная схема операции
Для моделирования суммы двоичных чисел с количеством разрядов больше единицы полусумматора недостаточно. Сложение необходимо осуществлять потактно, расположив несколько полусумматоров так, чтобы выход одного из них являлся одним из трех входов следующего. При этом образуется так называемый сумматор на три входа. Вход Р на рис. 1.8 ответственен за передачу разряда из младшего разряда.
Рис. 1.8. Cумматор на три входа
В табл. 1.3 приведено сложение одноразрядных чисел с учетом переноса разряда:
Таблица 1.3 Сложение одноразрядных чисел с учетом переноса разряда
После минимизации функции
Одной из важных технических проблем является разбиение процесса функционирования полученного устройства таким образом, чтобы в отдельный момент времени рассматривался один сумматор. Частота, с которой подключаются отдельные блоки, ответственные за один разряд, называется тактовой. Процесс усовершенствования ЭВМ сопровождается увеличением тактовой частоты, что связано с прогрессом в технологии изготовления ключей. На рис. 1.9 изображена схема из четырех сумматоров (так называемая линейка). Начальный вход равен нулю. На каждом такте вычисляются выходы
Рис. 1.9. Линейка четырех сумматоров с тремя входами
Пример. 1001 + 0101 =? Младший (нулевой) разряд:
Первый разряд: Второй разряд: Третий разряд: Четвертый разряд: Итак, 1001 + 0101 = 01110. Для моделирования умножения необходимо ввести еще одну операцию – сдвиг влево на разряд, что соответствует умножению на 2, т.е. умножению на 10 в двоичной системе счисления. Пример. 101101010 * 2 = 101101010 + 101101010 = 1011010100. Располагая рассмотренными возможностями моделирования, можно реализовать перевод чисел из десятичной системы счисления в двоичную. Предположим, что на клавиатуре набрана цифра 7. С ней сопоставляется двоичное число 111, что должно быть известно заранее. Пусть после этого набрана цифра 4. На экране дисплея возникает число 74. Представим это число в следующем виде: 7*10 + + 4. Числу 10 в двоичной системе соответствует 1010. Умножим 111 на 1010:
Двоичным представлением числа 70 является 1000110. Далее необходимо прибавить число 4, представленное в двоичной системе:
Если далее набрать цифру 9, то на экране возникнет число 749. Для перевода его в двоичную систему достаточно представить это число в следующем виде: 749 = 74 * 10 + 9. Произведем умножение числа 74 на 10 в двоичной системе счисления:
Для записи числа 749 в двоичной системе к полученному результату достаточно прибавить 1001, что соответствует числу 9 в десятичной системе:
Итак, 749 Следует обратить внимание на то, что никаких делений на два и нахождения остатков выполнять не требуется.
Контрольное задание
Представить числа
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 ,
, 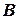 ,
,  :
: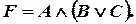


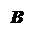
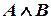
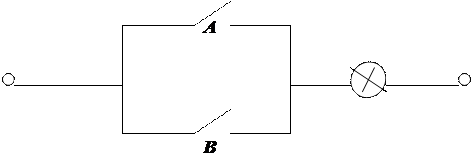
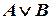

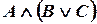
 ,
, 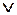 ) не образует полного базиса. Его следует дополнить отрицанием. Реализацию отрицания можно, например, получить с помощью так называемого реле, соответствующего каждому ключу. Нажатие кнопки должно замыкать простую цепь, содержащую соленоид. Если стандартное положение ключа открытое, то соленоид своим магнитным полем притягивает подвижную часть ключа до замыкания; если стандартное положение замкнутое, то включение магнитного поля приводит к размыканию, что и реализует функцию «отрицание».
) не образует полного базиса. Его следует дополнить отрицанием. Реализацию отрицания можно, например, получить с помощью так называемого реле, соответствующего каждому ключу. Нажатие кнопки должно замыкать простую цепь, содержащую соленоид. Если стандартное положение ключа открытое, то соленоид своим магнитным полем притягивает подвижную часть ключа до замыкания; если стандартное положение замкнутое, то включение магнитного поля приводит к размыканию, что и реализует функцию «отрицание». .
. .
. и
и  .
.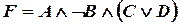 .
.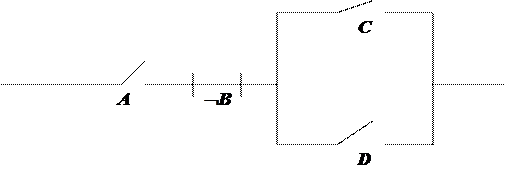 Результат показан на рис. 1.5.
Результат показан на рис. 1.5.



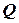
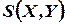 и
и  . Первая функция определяет содержимое младшего разряда результата сложения, а вторая – старшего. Соответствующая структурная схема имеет вид, показанный на рис. 1.6.
. Первая функция определяет содержимое младшего разряда результата сложения, а вторая – старшего. Соответствующая структурная схема имеет вид, показанный на рис. 1.6.
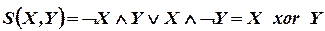 ,
,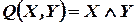 .
.
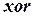

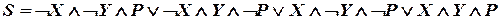 ;
;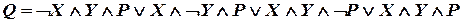 .
.
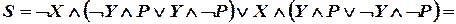

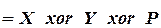 ;
;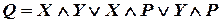 .
.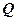 . Выход
. Выход 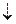
 P2
P2
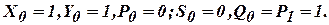
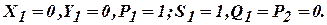
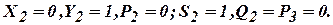
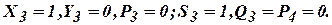
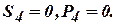
 1011101101 (в двоичной системе счисления).
1011101101 (в двоичной системе счисления). и
и 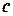 в двоичной системе счисления, сложить и перемножить их в двоичной системе. Результаты проверить.
в двоичной системе счисления, сложить и перемножить их в двоичной системе. Результаты проверить.