Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логика как наука, ее предмет, структура, значение.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Логика как наука, ее предмет, структура, значение. Логика – наука о правилах рассуждения и тех формах, в которых оно осуществляется. Предмет: мышление как средство познания объективного мира, те его формы и законы, в которых происходит отражение мира в процессе мышления. Основная цель: выяснение условий достижения истинных знаний и изучение внутренней структуры мыслительного процесса. Структура: 1) Общая (несимволическая); · Учение об основных формах мышления (понятия, суждения, умозаключения; · Систематические формы: определение, классификация, доказательства, логические методы, связанные с анализом данных опыта 2) Символическая (математическая).
Виды логик. 1) Философская 2) Математическая логика – изучает логические связи и отношения, лежащие в основе дедуктивного (логического) вывода. Разрабатывает применение математических методов к анализу форм и законов доказательного рассуждения. · Классическая логика – приписывает лишь одно из 2-ух значений: истина либо ложь. · Неклассическая логика – исключает применение двузначной логики в рассуждениях о бесконечных множествах. o Трёхзначная – высказываниям приписываются три значения: истина, ложь, нейтрально. o Многозначная – высказываниям может приписываться множество значений, например: вероятность, возможность, невероятность и т.д. Понятие как форма мышления. Понятие – форма мышления, в которой отражаются существенные признаки предмета или класса однородных предметов. Признак понятия: мысли о свойствах и отношениях предметов. · Существенное понятие (предмет не может существовать); · Несущественное понятие (предмет остаётся самим собой). Понятие состоит из: · Количественное (объём); · Качественное (содержание). Понятие и представление. Понятие и термин. Определение и структура понятия. Представление – чувственный образ предмета, в данный момент нами не воспринимаемого, но который ранее в той или иной форме воспринимался. Бывает воспроизводящее (представление чего-то, что мы когда-то видели) и творческое (наоборот). Термин – слово, предназначенное для максимально строгого и точного выражения тех или иных понятий. Определение понятия – логическая операция, которая раскрывает содержание понятия либо устанавливает значение термина (нужно для указания на сущность отражаемых в понятии предметов, раскрытия содержания понятия и отличия одного круга предметов от другого). Структура понятия: · Объём – совокупность предметов (класс), объединённых в этом понятии. Бывает конечный или бесконечный. · Содержание – множество признаков предмета, объединённых в одном понятии. (например: понятие – ромб, его содержание – «быть параллелограммом», «иметь равные стороны»). Содержание и объем понятия. · Объём – совокупность предметов (класс), объединённых в этом понятии. Бывает конечный или бесконечный. · Содержание – множество признаков предмета, объединённых в одном понятии. (например: понятие – ромб, его содержание – «быть параллелограммом», «иметь равные стороны»). Виды понятий. Классификация по объёму: · Единичные (понятия, соответствующие классам (множествам), состоящим из одного элемента). · Общие (понятия, соответствующие классам (множествам), состоящим из двух и более элементов). · Пустые (понятия, соответствующие классам (множествам), объёмы которых представляют собой классы реально не существующих предметов). Классификация по содержанию: · Конкретные (отражают одно- и многоэлементные классы предметов) и абстрактные (мыслится не сам предмет, а какой-то из его признаков) · Относительные (мыслятся предметы, существование одного из которых предполагает существование другого) и безотносительные (существующие самостоятельно) · Собирательные (класс однородных предметов мыслится как единое целое) и несобирательные (содержание можно отнести к каждому предмету данного) · Положительные (наличие у предмета качества или свойства) и отрицательные (указывается на отсутствие у предмета этого свойства) Классификация понятий. Классификация – разновидность деления понятий, представляет собой вид последовательного деления и образует развёрнутую систему, в которой каждый её член (вид) делится на подвиды и т.д. · По видообразующему признаку (зеркала бывают плоские и сферические) · Дихотомическая o По существенным признакам (естественная) o По несущественным (вспомогательная) Суждение. Виды суждений. Суждение – форма мышления, в которой утверждается или обращается что-либо относительно предметов и явлений, их св-в, связей и отношений и которая обладает св-вом выражать либо истину, либо ложь. Виды суждений: 1) Простое – 1 субъект и 1 предикат; 2) Сложное – состоят из неск. простых суждений, соединённых логическими союзами «и», «или», «если», «то». По объёму субъекта: 1) Единичные (это S есть/не есть P); 2) Частные: · Неопределённые (некоторые S есть P); · Определённые (только некоторые S или P) 3) Общие (в которых что-либо утверждается или отрицается в каждом предмете данного класса) (все S есть P или ни одно S не есть P) По качеству связи: 1) Утвердительные; 2) Отрицательные По содержанию предиката: 1) Суждения свойства ((не)принадлежность предмету мыслимого или иного свойства, состояние S есть P или S не есть P) 2) Суждения отношения – различные связи между предметами мысли по месту, времени, величине и пр. 3) Суждения существования – решают вопрос о наличии предмета нашей мысли – любого явления природы, общества.
Объединенная классификация суждений по качеству и количеству. Объединённая классификация суждений: 1) Общеутвердительные (все S есть P); 2) Общеотрицательные (ни одно S не есть P); 3) Частноутвердительные (некоторые S есть P); 4) Частноотрицательные (некоторые S не есть P).
Виды суждений, не рассматриваемых в классической логике. ??????????????????????? Комплексный анализ простого категорического суждения. Проведение комплексного анализа суждения предполагает, что: 1. Определена его логическая структура (форма); 2. Показано на круговой схеме соотношение объёмов дескриптивных терминов (субъекта и предиката) в составе суждения; 3. Указана распределённость терминов в составе суждения, на основании чего суждение отнесено к одному из четырёх типов (видов) и суждению сопоставлено условное буквенное обозначение. 12. Умозаключение. Умозаключение — форма мышления, в ходе которой из одного или нескольких суждений, называемых посылками, выводится суждение, заключающее в себе новое знание. (заключение) Дедуктивные умозаключения. Между его посылками и заключением есть отношение логического следования. Процесс рассуждения направлен от общего к частному. Силогистика. Основные понятия. Силогизм - дедуктивное умозаключение,в котором вывод совершается на основе соотношения терминов в одном или более категорических суждениях. Категорический силлогизм — это вид дедуктивного умозаключения, в котором из двух истинных категорических суждений, выводится новое категорическое суждение. В составе категорического силлогизма имеются две посылки и заключение. Все металлы (М) электропроводны (Р) — большая посылка. Медь ( S) есть металл (М) — меньшая посылка. Медь (S) электропроводна (Р) — заключение. Условный силлогизм - обе посылки и заключение – условные суждения. Условно-категорический силлогизм - одна посылка - условное суждение, а другая и заключение – категорическими. Разделительный силлогизм – 1 посылка – разделительное суждение, 2 посылка и заключение – разделительное и категорическое суждения. А) разделительно-категорический (1 пос. – разделит., 2 и заключ. – категор.) Б) условно-разделительный (1 из 2 или более – условное суждение, а 2 – разделительное суждение)
Суждения и высказывания как формы мышления. Суждение – форма мышления, в которой утверждается или отрицается что-либо относительно предметов и явлений, их свойств, связей и отношений и которая обладает свойством выражать либо истину, либо ложь. Высказывание – повествовательное предложение, которое может быть либо истинным, либо ложным. Основные операции над высказыванием. Таблица истинности. Операции задаются с помощью таблиц истинности. Отрицание
Конъюнкция – аналог «и».
Импликация – аналог «если, то».
Эквивалентность – аналог связки «тогда и только тогда».
Дизъюнкция – аналог «или».
Бином Ньютона» (a + b) n = an + Cn 1 an -1 b + Cn 2 an -2 bn -2 + Cn 3 an -3 b 3 + … + bn . Компоненты формулы «Бином Ньютона» · Первая часть формулы – разложение бинома · · Общий член разложения бинома n-й степени.
Где T – член разложения. (K+1)- порядковый номер разложения.
Треугольник Паскаля» Биномиальныекоэффициенты можно подучить с помощью треугольника Паскаля (пользуясь операцией сложения). В верхней строке пишутся две единицы. Все следующиестроки начинаются и оканчиваются единицей. Промежуточные числаполучаются сложением соседних чисел вышестоящей строки.
Практическая значимость треугольника Паскаля заключается в том, что с его помощью можно восстановить по памяти не только известные формулы, но и формулы куба суммы (разности), четвертой степени и выше. Пример: (a + b) 6 =a 6 +6a 5 b + 15a 4 b 2 +20a 3 b 3 + 15a 2 b 4 +6ab 5 +b 6.
Ориентированный граф - это граф, на ребрах которого обозначены разрешенные направления движения, проще говоря, расставлены стрелочки. Динамика Графа. Графы принято изображать в виде диаграмм, состоящих из точен или кружков и линий, соединяющих некоторые из этих точек (кружков) При этом точки соответствуют вершинам графа, а соединяющие пары точек линии — ребрам Матрица смежности Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента aijравно числу рёбер из i-й вершины графа в j-ю вершину. Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром (их инцидентность). В случае ориентированного графа каждому ребру <x,y> ставится в соответствие "-1" на позиции (x,y) и "1" на позиции (y,x); если связи между вершинами нет, то ставится в соответствие "0".
Изоморфизм графов. Два графа G и G, называются изоморфными если между множеством их вершин существует такое взаимно-однозначное соответствие, при котором в одном из графов ребрами соединены вершины в том и только в том случае, если в другом графе ребрами соединены те же вершины Для орграфов дуг также должна быть одинаковой.
Маршруты, цепи и циклы Маршрутом в графе G = <V,E; I> называется последовательность вершин и рёбер вида v 0 ,e 1 ,v 1 ,e 2,..., vn- 1 ,en,vn, где vi V, i [0 ,n ], ei E, (vi- 1 ,ei), (vi,ei) I, i [1 ,n ]. Вершины v 0, vn называются связанными данным маршрутом (или просто связанными). Вершину v 0 называют началом, а vn – концом маршрута. Если v 0 = vn, то маршрут называют замкнутым. Число n называется длиной маршрута. (Цепь, простая цепь, цикл). Маршрут, в котором все рёбра попарно различны, называется цепью. Замкнутый маршрут, являющийся цепью, называется циклом. Маршрут, в котором все вершины попарно различны, называется простой цепью. Цикл, в котором все вершины, кроме первой и последней, попарно различны, называется простым циклом. Операции над графами. Приводятся основные операции над графами такие как объединение, пересечение, кольцевая сумма, удаление вершины, удаление ребра, замыкание и стягивание. Эти операции рассматриваются для представления графов матрицами смежности. Цель лекции: Дать представление об операциях над графами и возможных способах их представления в матричных структурах. Рассмотрим семь операций над графами, три из которых являются бинарными, включающими два графа, а остальные четыре – унарные, т. е. определены на одном графе. Объединение графов G1 и G2, обозначаемое как
Пересечение графов G1 и G2, обозначаемое как
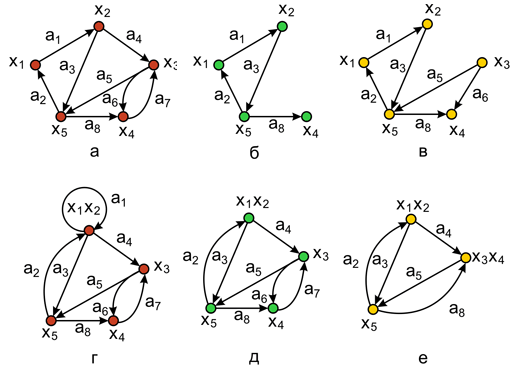
Рис.2.2. Операция пересечения и кольцевой суммы: а – граф G1; б – граф G2; в – граф Кольцевая сумма двух графов G1 и G2, обозначаемая как Легко убедиться в том, что три рассмотренные операции коммутативны т. е.
Удаление вершины. Если хi -вершина графа G = (X, A), то G–хi -порожденный подграф графа G на множестве вершин X–хi, т. е. G–хi является графом, получившимся после удаления из графа G вершины хi и всех ребер, инцидентных этой вершине. Удаление вершины х3 показано на рис. 2.3,б (для исходного графа, изображенного на рис. 2.3,а). Матрица смежности исходного графа представлена на таблице 2.1а). Результирующая матрица смежности графа после выполнения операции удаления вершины хi получается путем удаления соответствующего i - го столбца и i -ой строки из исходной матрицы и "сжимания" матрицы по вертикали и горизонтали начиная с (i+1) - го столбца и (i+1) -ой строки (таблица 2.1б). В дальнейшем элементы графа могут быть переобозначены.
Удаление ребра или удаление дуги. Если ai - дуга графа G = (X, A), то G-ai – подграф графа G, получающийся после удаления из G дуги ai. Заметим, что концевые вершины дуги ai не удаляются. Удаление из графа множества вершин или дуг определяется как последовательное удаление определенных вершин или дуг. Удаление дуг a4 и a7 показано на рис. 2.3,в. Результирующая матрица смежности графа после выполнения операции удаления дуги ai получается путем удаления соответствующих элементов из исходной матрицы (таблица 2.1в).
Замыкание или отождествление. Говорят, что пара вершин хi и xj в графе G замыкается (или отождествляется), если они заменяются такой новой вершиной, что все дуги в графе G, инцидентные хi и xj, становятся инцидентными новой вершине. Например, результат замыкания вершины х1 и х2показан на рис. 2.3,г для графа G (рис. 2.3,а). Матрица смежности графа после выполнения операции замыкания вершин хi и xj получается путем поэлементного логического сложения i - го и j - го столбцов и i -ой и j - строк в исходной матрице и "сжимания" матрицы по вертикали и горизонтали (таблица 2.1г). Стягивание. Под стягиванием подразумевают операцию удаления дуги или ребра и отождествление его концевых вершин. Граф, изображенный на рис. 2.3,д получен стягиванием дуги a1, а на рис. 2.3,е – стягиванием дуг a1, a6 и a7. Соответствующие результирующие матрицы смежности показаны в таблицах 2.1д и 2.1е. Деревья Деревом называется связный граф, не содержащий циклов Так как любой граф без циклов называется ациклическим (или лесом), то компонентами леса являются деревья. Ориентированным деревом (или ордеревом) называется ориентированный граф без циклов, во все вершины которого, кроме одной, ровно одна дуга. Единственная вершина, из которой дуги только выходят, называется корнем дерева. Остальные вершины называются узлами дерева. Из определения дерева следует, что корень связан единственным путем с любой другой вершиной дерева. На рисунке приведены диаграммы всех неизоморфных ориентированных деревьев с тремя и четырьмя вершинами. Висячая вершина ордерева называется листом. Путь из корня в лист называется ветвью.Длина наибольшей ветви ордерева называется высотой ордерева. Расстояние от корня до некоторой вершины называется уровнем вершины. Сам корень имеет уровень 0. Вершины одного уровня образуют ярус дерева. Замечание. При изображении ориентированных деревьев принято помещать корень наверху и все стрелки дуг ориентировать сверху вниз, что избавляет от необходимости изображать эти стреДеревья ориентированные На рисунке показано дерево, изображенное в соответствии с указанными выше правилами Вершины дерева разбиты на 4 яруса. Нулевой ярус содержит корень дерева х, В первом ярусе 3 вершины, во втором ярусе 5 вершин, в третьем ярусе-6 вершин Деревья бинарные и сбалансированные Бинарным деревом называется ориентированное дерево, из каждой вершины которого выходит не более двух дуг. Бинарное дерево называется сбалансированным деревом в том и только в том случае, если высоты двух поддеревьев каждой из вершин дерева отличаются не более, чем на единицу. Сбалансированные деревья иногда называют АВЛ деревьями, в соответствии с именами их первооткрывателей, советских математиков: Адельсона-Вельского и Ландиса, которые предложили в 1962 году данное определение. Разрезы Пусть G(V,U) –неориентированный граф. Разрезом называется всякое множество R ребер графа G, что удаление этих ребер из графа делает его несвязным. Разрез называется простым, если никакое собственное подмножество разрезом не является.
Потоковые модели. Социометрические модели.
Логика как наука, ее предмет, структура, значение. Логика – наука о правилах рассуждения и тех формах, в которых оно осуществляется. Предмет: мышление как средство познания объективного мира, те его формы и законы, в которых происходит отражение мира в процессе мышления. Основная цель: выяснение условий достижения истинных знаний и изучение внутренней структуры мыслительного процесса. Структура: 1) Общая (несимволическая); · Учение об основных формах мышления (понятия, суждения, умозаключения; · Систематические формы: определение, классификация, доказательства, логические методы, связанные с анализом данных опыта 2) Символическая (математическая).
Виды логик. 1) Философская 2) Математическая логика – изучает логические связи и отношения, лежащие в основе дедуктивного (логического) вывода. Разрабатывает применение математических методов к анализу форм и законов доказательного рассуждения. · Классическая логика – приписывает лишь одно из 2-ух значений: истина либо ложь. · Неклассическая логика – исключает применение двузначной логики в рассуждениях о бесконечных множествах. o Трёхзначная – высказываниям приписываются три значения: истина, ложь, нейтрально. o Многозначная – высказываниям может приписываться множество значений, например: вероятность, возможность, невероятность и т.д. Понятие как форма мышления. Понятие – форма мышления, в которой отражаются существенные признаки предмета или класса однородных предметов. Признак понятия: мысли о свойствах и отношениях предметов. · Существенное понятие (предмет не может существовать); · Несущественное понятие (предмет остаётся самим собой). Понятие состоит из: · Количественное (объём); · Качественное (содержание).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 3035; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.201.36 (0.013 с.) |

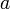

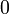

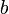
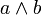


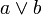
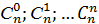 -,биномиальные коэффициенты
-,биномиальные коэффициенты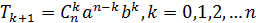

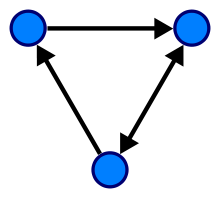 39. Ориентированные графы. Динамика графа. Матрицы смежности, инциденций и достижимости.
39. Ориентированные графы. Динамика графа. Матрицы смежности, инциденций и достижимости.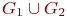 , представляет такой граф
, представляет такой граф 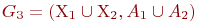 , что множество его вершин является объединением Х1 и Х2, а множество ребер – объединением A1 и A2. Граф G3, полученный операцией объединения графов G1 и G2, показан на рис. 2.1, а его матрица смежности – на рис. 2.1,е. Матрица смежности результирующего графа получается операцией поэлементного логического сложения матриц смежности исходных графов G1 и G2.
, что множество его вершин является объединением Х1 и Х2, а множество ребер – объединением A1 и A2. Граф G3, полученный операцией объединения графов G1 и G2, показан на рис. 2.1, а его матрица смежности – на рис. 2.1,е. Матрица смежности результирующего графа получается операцией поэлементного логического сложения матриц смежности исходных графов G1 и G2.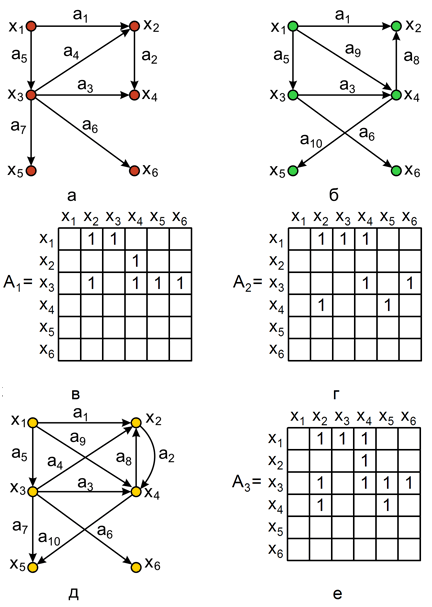
 , представляет собой граф
, представляет собой граф 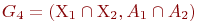 . Таким образом, множество вершин графа G4 состоит из вершин, присутствующих одновременно в G1 и G2. Операция пересечения графов
. Таким образом, множество вершин графа G4 состоит из вершин, присутствующих одновременно в G1 и G2. Операция пересечения графов 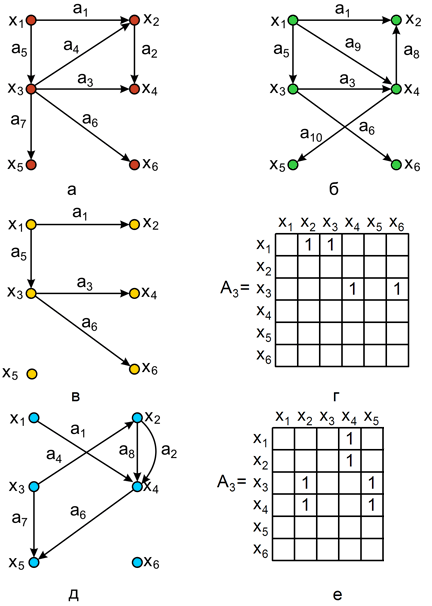
 ; е – матрица смежности графа
; е – матрица смежности графа  , представляет собой граф G5, порожденный на множестве ребер
, представляет собой граф G5, порожденный на множестве ребер  . Другими словами, граф G5 не имеет изолированных вершин и состоит только из ребер, присутствующих либо в G1, либо в G2, но не в обоих одновременно. Кольцевая сумма графов G1 и G2 показана на рис. 2.2,д, причем вершина
. Другими словами, граф G5 не имеет изолированных вершин и состоит только из ребер, присутствующих либо в G1, либо в G2, но не в обоих одновременно. Кольцевая сумма графов G1 и G2 показана на рис. 2.2,д, причем вершина 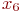 не входит в граф кольцевой суммы а результирующая матрица смежности получается операцией поэлементного логического сложения по mod 2 матриц смежности исходных графов G1 и G2. показана нарис. 2.2.е.
не входит в граф кольцевой суммы а результирующая матрица смежности получается операцией поэлементного логического сложения по mod 2 матриц смежности исходных графов G1 и G2. показана нарис. 2.2.е.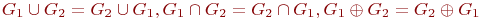 , и многоместны, т. е.
, и многоместны, т. е.  . и так далее.
. и так далее.