Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратная задача оценки постоянного срочногоСодержание книги
Поиск на нашем сайте
Аннуитета постнумерандо. В этом случае производится оценка будущих денежных поступлений с позиции текущего момента, под которым понимается момент времени, начиная с которого отсчитываются равные временные интервалы, входящие в аннуитет. Общая формула для оценки текущей стоимости срочного аннуитета постнумерандо выводится из ранее выведенной основной формулы и имеет вид:
Множитель
Экономический смысл дисконтного множителя Дисконтный множитель Из ранее выведенной формулы для определения множителя В случае рассмотрения только сложных процентов формулы для нахождения приведенных стоимостей аннуитетов аналогичны формулам для нахождения наращенных сумм. Получающиеся при этом денежные потоки будут представлять собой геометрические прогрессии, знаменателями которых будут соответствующие дисконтные множители. Так, для постоянного аннуитета постнумерандо с начислением сложных процентов m раз за базовый период приведенный денежный поток имеет вид:
Следовательно, приведенная стоимость такого аннуитета будет равна:
Для р-срочных аннуитетов с начислением сложных процентов соответственно один раз за базовый период и m раз за базовый период аналогичным образом можем получить следующие формулы для определения приведенной стоимости:
Пример. Страховая компания, заключив на 4 года договор с некоторой фирмой, получает от нее страховые взносы по 20 тыс. грн. в конце каждого полугодия. Эти взносы компания помещает в банк под 12% годовых. Необходимо найти приведенную стоимость суммы, которую получит страховая компания по данному контракту, если проценты будут начисляться: а) раз в полгода; б) ежемесячно. а) полугодовое начисление процентов: n = 4, r = 12%, m = 2, p = 2.
б) ежемесячное начисление процентов: n = 4, r = 12%, m = 12, p = 2.
Отсроченный аннуитет постнумерандо. В практике финансовых операций имеют место соглашения, когда первый из потока платежей начинает поступать не сразу, а через h периодов. Предположим, что платежи поступают в течение периодов и сложные проценты по ставке начисляются один раз в конце базового периода, совпадающего с периодом аннуитета. Стоимость этого аннуитета на начало периода, когда поступает первый платеж, находится по формуле Для этой цели используется следующая формула:
Из приведенной формулы видно, что приведенная стоимость отсроченного аннуитета представляет собой разность приведенных стоимостей аннуитетов с платежами, начиная с первого периода.
Пример. Банк предлагает ренту постнумерандо на 10 лет с ежеквартальной выплатой 100 грн. Годовая процентная ставка в течение всего периода остается постоянной. По какой цене можно приобрести такую ренту, если выплаты начнут осуществляться: а) немедленно; б) через 2 года; в) через 3,5 года, а процентная ставка равна 2, 4, 12% годовых.
а) вариант немедленного начала выплат. n = 10*4 = 40, r = 2%:4 = 0,5%.
б) вариант начала выплат через 2 года. N = 40, r = 4%: 4 = 1%, h = 2*4 = 8.
в) вариант начала выплат через 3,5 года. n = 40, r = 12%: 4 = 3%, h = 3,5 *4 = 14.
Из рассмотренного примера видно, что с ростом процентной ставки и срока, после которого начнутся выплаты, приведенная стоимость аннуитета уменьшается. Так, если выплаты начнутся через 3,5 года и процентная ставка составит 12% годовых, то указанную ренту можно приобретать за 1528,15 грн. или, естественно, дешевле. В то же время приведенная стоимость ренты с отсрочкой выплаты на 2 года и при процентной ставке 4% годовых составляет вдвое больше – 3032,23 грн. Как следует из формулы для определения будущей стоимости аннуитета постнумерандо в самом общем виде для нахождения
Если известна приведенная стоимость и остальные параметры, а необходимо найти величину разового платежа, то используется формула:
Величину разового платежа можно определить иначе. Мы помним, что
Аналогичным образом можно получить формулу для определения величины разового платежа (или поступления), если имеет место аннуитет постнумерандо и задана его приведенная стоимость. В этом случае формула имеет вид:
Пример. Работник заключает с фирмой контракт, согласно которому в случае его постоянной работы на фирме до выхода на пенсию в 65 лет фирма обязуется перечислять в конце каждого года в течение 20 лет на счет работника в банке одинаковые суммы, которые обеспечат работнику после выхода на пенсию ежегодные дополнительные выплаты в 6000 тыс. грн. в течение 15 лет. Какую сумму каждый год должна перечислять фирма, если работнику 45 лет и предполагается, что банк гарантирует годовую процентную ставку 10% годовых?
Зачастую при заключении финансовых контрактов имеют место случаи, когда заданы все остальные параметры, а необходимо определить срок действия аннуитета. В этом случае исходим из базовой формулы будущей стоимости аннуитета:
Из этой формулы путем несложных преобразований получим:
Если решается обратная задача оценки срочного аннуитета постнумерандо и необходимо определить срок действия такого аннуитета, то в этом случае применяется формула:
Пример. Предприятие хочет создать фонд в размере 200 тыс. грн. С этой целью в конце каждого года предприятие предполагает втосить по 50 тыс. грн. в банк под 18% годовых. Найти срок, необходимый для создания фонда.
Если известны все параметры аннуитета кроме величины процентной ставки, то в этом случае используется метод линейной интерполяции, так как непосредственно из ранее приведенных формул величину процентной ставки определить нельзя. Рассмотрим метод линейной интерполяции на конкретном примере. Пример. В течение 4-х лет предполагается создать резервный фонд в размере 20 тыс. грн., для чего будут производиться ежегодные взносы в банк в размере 4 тыс. грн. Необходимо определить размер процентной ставки при условии, что взносы и начисление на них процентов производится в конце года.
Прежде всего определим коэффициент наращения ренты, который равняется: По финансовым таблицам находим ближайшие значения факторного множителя: Для расчета процентной ставки по методу линейной интерполяции используется формула:
где ставки;
Для условий нашего примера значение процентной ставки, обеспечивающей за указанный срок создание резервного фонда в заданном объеме рассчитывается по формуле:
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.165.82 (0.009 с.) |



 называется коэффициентом дисконтирования ренты и как сумма членов геометрической прогрессии равен величине:
называется коэффициентом дисконтирования ренты и как сумма членов геометрической прогрессии равен величине:
 заключается в следующем: он показывает, чему равна с позиции текущего момента стоимость аннуитета с регулярным денежным поступлением в размере одной денежной единицы, продолжающегося n равных периодов с заданной процентной ставкой r. Значения этого множителя табулированы в финансовых таблицах.
заключается в следующем: он показывает, чему равна с позиции текущего момента стоимость аннуитета с регулярным денежным поступлением в размере одной денежной единицы, продолжающегося n равных периодов с заданной процентной ставкой r. Значения этого множителя табулированы в финансовых таблицах.



 тыс. грн.
тыс. грн. тыс. грн.
тыс. грн. и затем, осуществляя учет полученной величины за периодов, определяем приведенную стоимость отсроченного аннуитета на начальный момент времени.
и затем, осуществляя учет полученной величины за периодов, определяем приведенную стоимость отсроченного аннуитета на начальный момент времени.
 грн.
грн.
 грн.
грн.
 грн.
грн.


 Значит,
Значит,  , откуда с помощью несложных преобразований, получим:
, откуда с помощью несложных преобразований, получим:

 грн.
грн. грн.
грн.


 года
года .
. и
и  .
.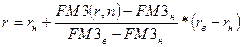
 нижнее и верхнее значение предполагаемой процентной
нижнее и верхнее значение предполагаемой процентной значения коэффициентов наращения при использовании процентных ставок
значения коэффициентов наращения при использовании процентных ставок  и
и  .
. или 15,09%.
или 15,09%.