Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение скалярного произведенияСодержание книги
Поиск на нашем сайте Пусть даны векторы Углом между двумя ненулевыми векторами Если хотя бы один из векторов Угол между векторами Определение5.1. Скалярным произведением двух ненулевых векторов Если хотя бы один из векторов Итак, по определению Пусть Аналогично доказывается справедливость равенства Заметим, что равенство (2) верно для любого ненулевого вектора Физический смысл скалярного произведения. Если вектор Два ненулевых вектора Если хотя бы один из векторов Теорема 5.1. Для ортогональности двух векторов Достаточность. Пусть
Во тором случае Необходимость. Если векторы ортогональны, то либо угол 𝜑 прямой, либо хотя бы один из векторов нулевой, но в любом случае Теорема 5.1 доказана. Теорема 5.2. Для любых векторов 1) 2) 3) 4) Свойство 1 следует из определения скалярного произведения. Действительно, если Докажем свойство 2. Рассмотрим случай, когда
Свойство 2 доказано. Докажем свойство 3. В случае, когда Докажем свойство 4. Из определения скалярного произведения следует, что Из последнего равенства следует справедливость свойства 4. Замечание. Свойства 2) и 3) называются свойством линейности скалярного произведения по первому множителю. Из свойства 1) следует, что скалярное произведение обладает свойством линейности и по второму множителю, т.е. Рассмотрим следующий вопрос: Как можно выразить скалярное произведение векторов Теорема 5.3. Если вектор
Доказательство. Представим векторы
Пользуясь свойствами скалярного произведения, получим
Учитывая в правой части последнего равенства, что
Теорема 5.3 доказана. Следствие. Для ортогональности двух векторов Справедливость этого утверждения непосредственно следует из теорем 5.1 и 5.3. Пусть
С другой стороны
Если
|
||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 112; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

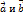 . Приложим эти векторы к одной точке
. Приложим эти векторы к одной точке  , и пусть
, и пусть  ,
, 
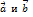 называется наименьший угол между лучами
называется наименьший угол между лучами  и
и 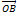 .
.
 нулевой, то угол между векторами
нулевой, то угол между векторами  и
и 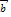 обозначается через 𝜑 или
обозначается через 𝜑 или  . Очевидно, что
. Очевидно, что  .
.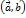 .
. .
. – проекцию вектора
– проекцию вектора  на ось, определяемую ненулевым вектором
на ось, определяемую ненулевым вектором 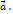 Тогда в силу теоремы 4.1 настоящей главы
Тогда в силу теоремы 4.1 настоящей главы 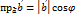 , где 𝜑 – угол между векторами
, где 𝜑 – угол между векторами  Следовательно равенство (1) может быть записано в виде
Следовательно равенство (1) может быть записано в виде 
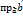
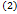 .
. 

 и любого
и любого  вектора
вектора  , в том числе нулевого. И равенство (3) верно для любого ненулевого вектора
, в том числе нулевого. И равенство (3) верно для любого ненулевого вектора 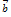 и любого вектора
и любого вектора 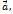 в том числе нулевого.
в том числе нулевого. изображает силу, точкаприложения которой перемещается из начала в конец вектора,
изображает силу, точкаприложения которой перемещается из начала в конец вектора, 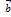 то работа, производимая этой силой равна скалярному произведению
то работа, производимая этой силой равна скалярному произведению  называются ортогональными (или перпендикулярными), если угол 𝜑 между ними является прямым.
называются ортогональными (или перпендикулярными), если угол 𝜑 между ними является прямым. является нулевым, то эти векторы также считаются ортогональными.
является нулевым, то эти векторы также считаются ортогональными. . Тогда в силу определения скалярного произведения
. Тогда в силу определения скалярного произведения . Из последнего равенства мы имеем либо 1)
. Из последнего равенства мы имеем либо 1)  либо 2)
либо 2)  . В первом случае хотя бы один из векторов нулевой, и тогда векторы считаются ортогональными по определению.
. В первом случае хотя бы один из векторов нулевой, и тогда векторы считаются ортогональными по определению.

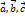 и числа
и числа 
 ;
; ;
;
 , если
, если  , если
, если  .
. - нулевой вектор. Тогда
- нулевой вектор. Тогда  ,
,  и
и  =
=  . В этом случае справедливость свойства 2 очевидна. Пусть теперь
. В этом случае справедливость свойства 2 очевидна. Пусть теперь  - ненулевой вектор. Тогда согласно теореме 4.5 §4 главы 3
- ненулевой вектор. Тогда согласно теореме 4.5 §4 главы 3
 нулевой вектор, справедливость свойства 3 очевидна. Пусть
нулевой вектор, справедливость свойства 3 очевидна. Пусть  - ненулевой вектор, тогда
- ненулевой вектор, тогда  . Свойство 3 доказано.
. Свойство 3 доказано.
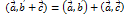 и
и  для любых векторов
для любых векторов 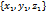 , а
, а 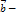 координаты
координаты 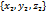 , то скалярное произведение
, то скалярное произведение 
 ,
, 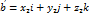 . Тогда
. Тогда


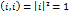 ,
, 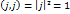 ,
, 
 , получим
, получим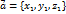 и
и  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 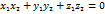 .
. - прямоугольные декартовы координаты вектора
- прямоугольные декартовы координаты вектора  в прямоугольной системе координат
в прямоугольной системе координат 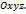
 . Согласно теореме 5.3
. Согласно теореме 5.3
 . Следовательно
. Следовательно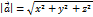
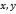 - прямоугольные координаты вектора
- прямоугольные координаты вектора 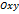 , то
, то