Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценивание параметров классической линейной модели множественной регрессии.
На любой экономический показатель чаще всего оказывает влияние не один, а несколько факторов. В этом случае рассматривается множественная регрессия. Теоретическое линейное уравнение регрессии имеет вид: Параметр α называется свободным членом и определяет значение y в случае, когда все объясняющие переменные равны нулю. Однако, как и в случае парной регрессии, факторы по своему экономическому содержанию часто не могут принимать нулевых значений, и значение свободного члена не имеет экономического смысла. При этом в отличие от парной регрессии, значение каждого регрессионного коэффициента Для проведения анализа в рамках линейной модели множественной регрессии необходимо выполнение ряда предпосылок МНК: 10. E (εi) = 0 (i =1,..., n) - гомоскедастичность остатков (состояние, при котором измерения вариативности колеблются внутри ожидаемого диапазона). 20. 30. X 1,...Х- неслучайные величины. 40. Модель является линейной относительно параметров. 50. Отсутствие мультиколлинеарности: между объясняющими переменными отсутствует строгая линейная зависимость. 60. Ошибки Модель (1.1), в которой зависимая переменная у i ,, возмущения ε i и объясняющие переменные Самым распространенным методом решения этой задачи является метод наименьших квадратов (МНК). Его суть состоит в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной y от её значений
Рассмотрим три метода расчета параметров множественной линейной регрессии. 1. Матричный метод. Представим данные наблюдений и параметры модели в матричной форме.
Значения независимых переменных запишем в виде прямоугольной матрицы размерности В этих обозначениях эмпирическое уравнение регрессии выглядит так: Y = XB + e Отсюда вектор остатков регрессии можно выразить таким образом: e = Y - XB Тогда, функционал (При выводе использовались формулы В соответствии с МНК дифференцирование Q по вектору В приводит к выражению:
2. Скалярный метод. При его применении строится система нормальных уравнений (1.4), решение которой и позволяет получить оценки параметров регрессии. Решить систему можно любым способом, например, методом определителей или методом Гаусса.
2. Регрессионная модель в стандартизованном масштабе. Уравнение регрессии в стандартизованном масштабе имеет вид:
Применяя МНК к уравнению (1.2), после соответствующих преобразований получим систему нормальных уравнений:
Сравнивая коэффициенты β j между собой, можно ранжировать факторы по силе их воздействия на результат, а также использовать коэффициенты при отсеве факторов – из модели исключаются факторы с наименьшим значением β j. В этом основное достоинство стандартизованных коэффициентов регрессии, в отличие от коэффициентов обычной регрессии, которые несравнимы между собой. Подобно тому, как в парной зависимости коэффициенты регрессии и корреляции связаны между собой, так и во множественной регрессии коэффициенты «чистой» регрессии bj связаны с β – коэффициентами: От уравнения регрессии в стандартизованном масштабе можно перейти к уравнению регрессии, причем параметр а определяется как Теорема Гаусса – Маркова: При выполнимости всех предпосылок регрессионного анализа оценки
|
||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 85; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.226.26 (0.009 с.) |
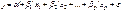 . (1.1)
. (1.1)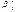 равно среднему изменению y при увеличении x j на одну единицу лишь при условии, что все остальные факторы остались неизменными. Величина ε представляет собой случайную ошибку регрессионной зависимости.
равно среднему изменению y при увеличении x j на одну единицу лишь при условии, что все остальные факторы остались неизменными. Величина ε представляет собой случайную ошибку регрессионной зависимости.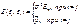 - отсутствие автокорреляции (статистическая взаимосвязь между последовательностями величин одного ряда, взятых со сдвигом)
- отсутствие автокорреляции (статистическая взаимосвязь между последовательностями величин одного ряда, взятых со сдвигом)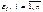 имеют нормальное распределение
имеют нормальное распределение 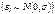 . Выполнимость этого условия нужна для проверки статистических гипотез и построения интервальных оценок.
. Выполнимость этого условия нужна для проверки статистических гипотез и построения интервальных оценок.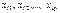 удовлетворяют предпосылкам регрессионного анализа называется классической нормальной линейной моделью множественной регрессии (НКЛММР).
удовлетворяют предпосылкам регрессионного анализа называется классической нормальной линейной моделью множественной регрессии (НКЛММР).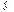 , получаемых по уравнению регрессии. Поскольку
, получаемых по уравнению регрессии. Поскольку  - оценки теоретических значений
- оценки теоретических значений 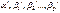 , или эмпирические коэффициенты регрессии, е – оценка отклонения ε. Тогда расчетное выражение имеет вид:
, или эмпирические коэффициенты регрессии, е – оценка отклонения ε. Тогда расчетное выражение имеет вид: 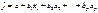 . (1.2)
. (1.2)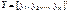 - n – мерный транспонированный вектор – столбец наблюдений зависимой переменной;
- n – мерный транспонированный вектор – столбец наблюдений зависимой переменной;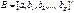 - (p +1) – мерный транспонированный вектор – столбец параметров уравнения регрессии (1.2);
- (p +1) – мерный транспонированный вектор – столбец параметров уравнения регрессии (1.2);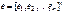 - n – мерный транспонированный вектор – столбец отклонений выборочных значений yi.
- n – мерный транспонированный вектор – столбец отклонений выборочных значений yi.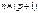 :
: 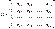 Каждому столбцу этой матрицы отвечает набор из n значений одного из факторов, а первый столбец состоит из единиц, которые соответствуют значениям переменной при свободном члене.
Каждому столбцу этой матрицы отвечает набор из n значений одного из факторов, а первый столбец состоит из единиц, которые соответствуют значениям переменной при свободном члене.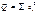 , который, минимизируется по МНК, можно записать как произведение вектора – строки e ’ на вектор – столбец e:
, который, минимизируется по МНК, можно записать как произведение вектора – строки e ’ на вектор – столбец e: 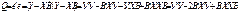
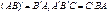 ).
).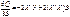 , которое для нахождения экстремума следует приравнять к нулю. В результате преобразований получаем выражение для вектора параметров регрессии:
, которое для нахождения экстремума следует приравнять к нулю. В результате преобразований получаем выражение для вектора параметров регрессии:  . (1.3)
. (1.3)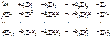 .
.  , (1.5) где
, (1.5) где 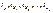 - стандартизованные переменные:
- стандартизованные переменные: ,для которых среднее значение равно нулю:
,для которых среднее значение равно нулю: 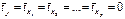 , а среднее квадратическое отклонение равно единице:
, а среднее квадратическое отклонение равно единице: 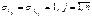 ; β j – стандартизованные коэффициенты регрессии, которые показывают, на сколько значений с.к.о. изменится в среднем результат, если соответствующий фактор х j изменится на одну с.к.о. при неизменном среднем уровне других факторов.
; β j – стандартизованные коэффициенты регрессии, которые показывают, на сколько значений с.к.о. изменится в среднем результат, если соответствующий фактор х j изменится на одну с.к.о. при неизменном среднем уровне других факторов.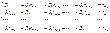 В этой системе
В этой системе 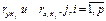 - элементы расширенной матрицы парных коэффициентов корреляции или, другими словами, коэффициенты парной корреляции между различными факторами или между факторами и результативным признаком.
- элементы расширенной матрицы парных коэффициентов корреляции или, другими словами, коэффициенты парной корреляции между различными факторами или между факторами и результативным признаком.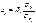 .
.
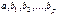 , полученные по МНК, являются наиболее эффективными (в смысле наименьшей дисперсии) в классе линейных несмещенных оценок.
, полученные по МНК, являются наиболее эффективными (в смысле наименьшей дисперсии) в классе линейных несмещенных оценок.