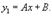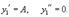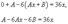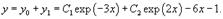Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула полной вероятности, формула Байеса.
Теорема. Вероятность события B, которое может наступить только при условии появления одного из событий A1, A2, A3, …, An, образующих полную группу попарно несовместных событий, равна сумме произведений вероятностей каждого из событий A1, A2, A3, …, An на соответствующую условную вероятность события B, т.е. Р(B) = Р(Ai) РAi(B). (1) Согласно условию теоремы, событие B может наступить, если появится одно из событий A1, A2, A3, …, An. Это означает, что появление события B влечет появление одного из событий A1B, A2B, A3B, …, AnB, неважно какого. Поэтому событие B можно представить в виде B = A1B + A2B + A3B + … + AnB. Так как события A1, A2, A3, …, An, по условию, попарно несовместимы, то, очевидно, несовместны и события A1B, A2B, A3B, …, AnB. Тогда, применяя теорему сложения для несовместных событий, получаем Р(B) = Р(A1B) + Р(A2B) + Р(A3B) + … + Р(AnB) Далее, по теореме умножения вероятностей, можно записать Р(B)=Р(A1)РA1(B)+Р(A2)РA2(B)+Р(A3)РA3(B)+ … + Р(An)РAn(B)=Р(Ai)РAi(B). Формула (1), в справедливости которой убеждает доказанная теорема, называется формулой полной вероятности, а события A1, A2, A3, …, An – гипотезами. Пример. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта. Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через Можно применить формулу полной вероятности, причем в наших обозначениях:
При выводе формулы полной вероятности предполагалось, что событие B, вероятность которого следовало определить, могло произойти с одним из событий A1, A2, A3, …, An, образующих полную группу, при этом вероятности указанных событий (гипотез) были заранее известны. Предположим, что проведен опыт и событие B наступило. Установим, как изменяются после этого вероятности гипотез, т.е. найдем условную вероятность РA(B) для каждой гипотезы.
По теореме умножения (вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило Р(АВ)=Р(А)*РА(В)) имеем Р(BAi) = Р(B)РB(Ai) = Р(Ai) РАi(B), i=1, 2, 3, …, n, или Р(B)РB(Ai) = Р(Ai) РАi(B). Отсюда РB(Ai) = Р(Ai) РАi(B) / Р(B). Воспользовавшись формулой (1), имеем РB(Ai) = Р(Ai) РАi(B) / Р(Ai) РАi(B)
Полученная формула называется формулой Байеса или теоремой гипотез. Формула Байеса позволяет "пересмотреть" вероятности гипотез после того, как становится известным результат опыта, в результате которого появилось событие А. Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной. События, отражающие действие «причин», в данном случае обычно называют гипотезами, так как они — предполагаемые события, повлекшие данное. Безусловную вероятность справедливости гипотезы называют априорной (насколько вероятна причина вообще), а условную — с учетом факта произошедшего события — апостериорной (насколько вероятна причина оказалась с учетом данных о событии). Пример. Пусть вероятность брака у первого рабочего Cобытие
ЧТОБЫ ВСПОМНИТЬ: Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе. Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними. Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события. Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет. Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле: Вероятность произведения зависимых событий вычисляется по формуле условной вероятности. Условной вероятностью Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е. В частности, отсюда получаем Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Построение общего решения однородного уравнения. Нахождение частного решения неоднородного уравнения методом вариаций произвольных постоянных и методом неопределенных коэффициентов. Дифференциальное уравнение — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него. Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные y’(x), y’’(x), …, y(n)(x) до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многихпеременных. Линейным однородным дифференциальным уравнением n-го порядка с постоянными коэффициентами явл. уравнение вида:
Система функций y1, y2, …, yn-1, yn называется линейно независимой в интервале (a,b), если тождество c 1 y 1 + c 2 y 2 +…+ cnyn =0 (c1, c2,.., cn - постоянные числа) может выполняться только когда все ck=0 (такие решения yk можно сравнить с векторами на плоскости: есть векторы, которые нельзя выразить один через другой – это линейно независимые векторы. Все остальные векторы можно выразить через них с помощью умножения на любое число и сложение). Если к тому же каждая из функций yk является частным решением однородного уравнения, то система решений однородного уравнения называется фундаментальной системой решений. Если фундаментальная система решений найдена, то функция y = c 1 y 1 + c 2 y 2 +…+ cnyn дает общее решение однородного уравнения (все ck - константы).
Для нахождения частных решений составляют характеристическое уравнение 1) каждому действительному простому (некратному) корню k в общем решении соответствует слагаемое вида Cekx; 2) каждому действительному корню кратности m в общем решении соответствует слагаемое (C 1 + C 2 x +…+ Cmxm -1) ekx; 3) каждой паре комплексно сопряжённых простых корней k12=a±bi в общем решении соответствует слагаемое вида eax(C1cosbx+C2sinbx); 4) крастности m вида eax[(C1+C2x+…+Cm-1xm-1)cosbx]+[(C1’+C2’x+…+Cm-1’xm-1)sinbx]
Линейное неоднородное уравнение: Если u=u(x) – частное решение неоднородного уравнения, а y1, y2, …, yn – фундаментальная система решений соответствующего однородного, то общее решение неоднородного следует искать в виде y=u+C1y1+C2y2+…, то есть общее решение неоднородного уравнения есть сумма любого его частного решения и общего решения соответствующего однородного. Методы отыскания частного решения неоднородного: 1) Метод вариации произвольных постоянных. Пусть известна фундаментальная система решений y1, y2, y3… (общее решение однородного), то общее решение неоднородного ищется в виде u(x)=C1(x)y1+C2(x)y2+…+Cn(x)yn, где С1(x), C2(x), … Cn(x) находим из системы С’1(x)y1+C’2(x)y2+…+C’n(x)yn=0, С’1(x)y’1+C’2(x)y’2+…+C’n(x)y’n=0, … С’1(x)y1(n-2)+C’2(x)y2(n-2)+…+C’n(x)yn(n-2)=0, С’1(x)y1(n)+C’2(x)y2(n)+…+C’n(x)yn(n)=f(x), Находим c’i(x), интегрируем их, подставляем полученные первообразные ci(x) в общее решение неоднородного уравнения. 2) Метод неопределенных коэффициентов. Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов. Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как
В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель xs, где s − кратность корня α в характеристическом уравнении. В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x.
Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение.
Пример: Найти общее решение уравнения y'' + y' −6y = 36x. Решение. Воспользуемся методом неопределенных коэффициентов. Правая часть заданного уравнения представляет собой линейную функцию f(x) = ax + b. Поэтому будем искать частное решение в виде Производные равны: Подставляя это в дифференциальное уравнение, получаем: Последнее уравнение является тождеством, то есть справедливо для всех x, поэтому приравняем коэффициенты при слагаемых с одинаковыми степенями x в левой и правой части: Из полученной системы находим: A = −6, B = −1. В результате, частное решение записывается в виде y1=-6x-1 Теперь найдем общее решение однородного дифференциального уравнения. Вычислим корни вспомогательного характеристического уравнения: Следовательно, общее решение соответствующего однородного уравнения имеет вид: Итак, общее решение исходного неоднородного уравнения выражается формулой
|
||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.247.231 (0.042 с.) |
 обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.
обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям. Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:
Подставляя эти значения в формулу полной вероятности, получим искомую вероятность: 
 , у второго рабочего —
, у второго рабочего —  , а у третьего —
, а у третьего —  . Первый изготовил
. Первый изготовил  деталей, второй —
деталей, второй — 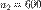 деталей, а третий —
деталей, а третий —  деталей. Начальник цеха берёт случайную деталь, и она оказывается бракованной. Спрашивается, с какой вероятностью эту деталь изготовил третий рабочий?
деталей. Начальник цеха берёт случайную деталь, и она оказывается бракованной. Спрашивается, с какой вероятностью эту деталь изготовил третий рабочий? — брак детали, событие
— брак детали, событие  — деталь произвёл рабочий
— деталь произвёл рабочий  . Тогда
. Тогда 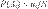 , где
, где  , а
, а  По формуле полной вероятности
По формуле полной вероятности  По формуле Байеса получим:
По формуле Байеса получим:


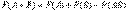 .
. .
. (два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
(два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
 .
.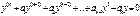 , гдеak – постоянные вещественные числа
, гдеak – постоянные вещественные числа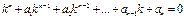 , которое получается заменой в нём производных искомой функции соответствующими степенями k, сама функция заменяется на единицу. Тогда общее решение строится в зависимости от характера корней:
, которое получается заменой в нём производных искомой функции соответствующими степенями k, сама функция заменяется на единицу. Тогда общее решение строится в зависимости от характера корней: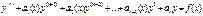

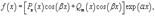 где Pn(x) и Qm(x) − многочлены степени n и m, соответственно.
где Pn(x) и Qm(x) − многочлены степени n и m, соответственно.