Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
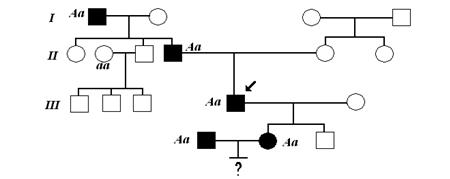
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимые и достаточные условия экстремума дважды непрерывно дифференцируемой функции и двух переменных.Стр 1 из 22Следующая ⇒
Экстремумы функций двух переменных Определение. Точка При этом значение Необходимый признак экстремума: Если в точке Для отыскания стационарных точек функции
Достаточные условия экстремума для функции нескольких переменных носят значительно более сложный характер, чем для функции одной переменной. Мы рассмотрим эти условия без доказательства только для функции двух переменных. Пусть точка
Если Если Пример. Найдём стационарные точки функции Система уравнений (1.1) имеет вид:
Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Построение общего решения однородного уравнения. Нахождение частного решения неоднородного уравнения методом вариаций произвольных постоянных и методом неопределенных коэффициентов.
Дифференциальное уравнение — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него. Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные y’(x), y’’(x), …, y(n)(x) до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многихпеременных. Линейным однородным дифференциальным уравнением n-го порядка с постоянными коэффициентами явл. уравнение вида:
Система функций y1, y2, …, yn-1, yn называется линейно независимой в интервале (a,b), если тождество c 1 y 1 + c 2 y 2 +…+ cnyn =0 (c1, c2,.., cn - постоянные числа) может выполняться только когда все ck=0 (такие решения yk можно сравнить с векторами на плоскости: есть векторы, которые нельзя выразить один через другой – это линейно независимые векторы. Все остальные векторы можно выразить через них с помощью умножения на любое число и сложение). Если к тому же каждая из функций yk является частным решением однородного уравнения, то система решений однородного уравнения называется фундаментальной системой решений. Если фундаментальная система решений найдена, то функция y = c 1 y 1 + c 2 y 2 +…+ cnyn дает общее решение однородного уравнения (все ck - константы). Для нахождения частных решений составляют характеристическое уравнение 1) каждому действительному простому (некратному) корню k в общем решении соответствует слагаемое вида Cekx;
2) каждому действительному корню кратности m в общем решении соответствует слагаемое (C 1 + C 2 x +…+ Cmxm -1) ekx; 3) каждой паре комплексно сопряжённых простых корней k12=a±bi в общем решении соответствует слагаемое вида eax(C1cosbx+C2sinbx); 4) крастности m вида eax[(C1+C2x+…+Cm-1xm-1)cosbx]+[(C1’+C2’x+…+Cm-1’xm-1)sinbx]
Линейное неоднородное уравнение: Если u=u(x) – частное решение неоднородного уравнения, а y1, y2, …, yn – фундаментальная система решений соответствующего однородного, то общее решение неоднородного следует искать в виде y=u+C1y1+C2y2+…, то есть общее решение неоднородного уравнения есть сумма любого его частного решения и общего решения соответствующего однородного. Методы отыскания частного решения неоднородного: 1) Метод вариации произвольных постоянных. Пусть известна фундаментальная система решений y1, y2, y3… (общее решение однородного), то общее решение неоднородного ищется в виде u(x)=C1(x)y1+C2(x)y2+…+Cn(x)yn, где С1(x), C2(x), … Cn(x) находим из системы С’1(x)y1+C’2(x)y2+…+C’n(x)yn=0, С’1(x)y’1+C’2(x)y’2+…+C’n(x)y’n=0, … С’1(x)y1(n-2)+C’2(x)y2(n-2)+…+C’n(x)yn(n-2)=0, С’1(x)y1(n)+C’2(x)y2(n)+…+C’n(x)yn(n)=f(x), Находим c’i(x), интегрируем их, подставляем полученные первообразные ci(x) в общее решение неоднородного уравнения. 2) Метод неопределенных коэффициентов. Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов. Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как
В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель xs, где s − кратность корня α в характеристическом уравнении. В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x. Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение.
Пример: Найти общее решение уравнения y'' + y' −6y = 36x. Решение. Воспользуемся методом неопределенных коэффициентов. Правая часть заданного уравнения представляет собой линейную функцию f(x) = ax + b. Поэтому будем искать частное решение в виде Производные равны: Подставляя это в дифференциальное уравнение, получаем: Последнее уравнение является тождеством, то есть справедливо для всех x, поэтому приравняем коэффициенты при слагаемых с одинаковыми степенями x в левой и правой части: Из полученной системы находим: A = −6, B = −1. В результате, частное решение записывается в виде y1=-6x-1 Теперь найдем общее решение однородного дифференциального уравнения. Вычислим корни вспомогательного характеристического уравнения: Следовательно, общее решение соответствующего однородного уравнения имеет вид: Итак, общее решение исходного неоднородного уравнения выражается формулой
Пример расчета межотраслевого баланса Рассмотрим 2 отрасли промышленности: производство угля и стали. Уголь требуется для производства стали, а некоторое количество стали — в виде инструментов — нужно для добычи угля. Предположим, что условия таковы: для производства 1 т стали нужно 3 т угля, а для 1 т угля — 0,1 т стали.
Отрасль Уголь Сталь Уголь 1 3 Сталь 0.1 1
Мы хотим, чтобы чистый выпуск угольной промышленности был 200 тыс. тонн угля, а чёрной металлургии — 50 тыс. тонн стали (это наши y1 и y2). Если каждая из них будет производить лишь 200 тыс. и 50 тыс. тонн, то часть продукции будет использоваться в другой отрасли (следовательно, на конечное потребление останется гораздо меньше угля и стали). Для производства 50 тыс. тонн стали требуется 50*3 = 150 тыс. тонн угля, а для производства 200 тыс. тонн угля нужно 200*0.1 = 20 тыс. тонн стали. Чистый выход будет равен: 200-150 = 50 тыс.тонн угля и 50-20 = 30 тыс. тонн стали. Нужно дополнительно производить уголь и сталь, чтобы использовать их в другой отрасли. Обозначим х1 — количество угля, х2 — количество стали. Валовый выпуск каждой продукции найдем из системы уравнений:
Типы входных данных 1. Признаковое описание объектов. Каждый объект описывается набором своих характеристик, называемых признаками. Признаки могут быть числовыми или нечисловыми. 2. Матрица расстояний между объектами. Каждый объект описывается расстояниями до всех остальных объектов метрического пространства. 3. Матрица сходства между объектами. Учитывается степень сходства объекта с другими объектами выборки в метрическом пространстве. Сходство здесь дополняет расстояние (различие) между объектами до 1. Можно встретить описание двух фундаментальных требований предъявляемых к данным — однородность и полнота. Однородность требует, чтобы все кластеризуемые сущности были одной природы, описываться сходным набором характеристик. Используется в археологии, медицине, психологии, химии, биологии, государственном управлении, филологии, антропологии, маркетинге, социологии и других дисциплинах.
Дискриминантный анализ — это раздел математической статистики, содержанием которого является разработка методов решения задач различения (дискриминации) объектов наблюдения по определенным признакам. Например, разбиение совокупности предприятий на несколько однородных групп по значениям каких-либо показателей производственно-хозяйственной деятельности.
Все процедуры дискриминантного анализа можно разбить на две группы и рассматривать их как совершенно самостоятельные методы. Первая группа процедур позволяет интерпретировать различия между существующими классами, вторая — проводить классификацию новых объектов в тех случаях, когда неизвестно заранее, к какому из существующих классов они принадлежат. Пусть имеется множество единиц наблюдения — генеральная совокупность. Каждая единица наблюдения характеризуется несколькими признаками (переменными) хij - значение j-й переменной у i-го объекта i = 1..N; j = 1..p. Предположим, что все множество объектов разбито на несколько подмножеств (два и более). Из каждого подмножества взята выборка объемом nk где k - номер подмножества (класса), k = 1..q. Признаки, которые используются для того, чтобы отличать один класс (подмножество) от другого, называются дискриминантными переменными. Каждая из этих переменных должна измеряться либо по интервальной шкале, либо по шкале отношений. Интервальная шкала позволяет количественно описать различия между свойствами объектов. Для задания шкалы устанавливаются произвольная точка отсчета и единица измерения. Примерами таких шкал являются календарное время, шкалы температур и т. п. В качестве оценки положения центра используются средняя величина, мода и медиана. Теоретически число дискриминантных переменных не ограничено, но на практике их выбор должен осуществляться на основании логического анализа исходной информации и одного из критериев. Число объектов наблюдения должно превышать число дискриминантных переменных, как минимум, на два, т. е. p < N. Дискриминантные переменные должны быть линейно независимыми. Еще одним предложением при дискриминантном анализе является нормальность закона распределения многомерной величины, т. е. каждая из дискриминантных переменных внутри каждого из рассматриваемых классов должна быть подчинена нормальному закону распределения. В случае, когда реальная картина в выборочных совокупностях отличается от выдвинутых предпосылок, следует решать вопрос о целесообразности использования процедур дискриминантного анализа для классификации новых наблюдений, т. к. в этом случае затрудняются расчеты каждого критерия классификации. Пример: Медик может регистрировать различные переменные, относящиеся к состоянию больного, чтобы выяснить, какие переменные лучше показывают, что пациент, вероятно, выздоровел полностью, частично или совсем не выздоровел.
Факторный анализ — многомерный метод, применяемый для изучения взаимосвязей между значениями переменных. Также это совокупность методов, которые на основе реально существующих связей признаков (или объектов) позволяют выявлять латентные обобщающие характеристики организационной структуры и механизма развития изучаемых явлений и процессов. Факторный анализ позволяет решить две важные проблемы исследователя: описать объект измерения всесторонне и в то же время компактно.
Таким образом можно выделить 2 цели Факторного анализа: 1. определение взаимосвязей между переменными, (классификация переменных); 2. сокращение числа переменных необходимых для описания данных. При анализе в один фактор (скрытую переменную) объединяются сильно коррелирующие между собой переменные, как следствие происходит перераспределение дисперсии между компонентами и получается максимально простая и наглядная структура факторов. После объединения коррелированность компонент внутри каждого фактора между собой будет выше, чем их коррелированность с компонентами из других факторов. Эта процедура также позволяет выделить латентные переменные, что бывает особенно важно при анализе социальных представлений и ценностей. Например, анализируя оценки, полученные по нескольким шкалам, исследователь замечает, что они сходны между собой и имеют высокий коэффициент корреляции, он может предположить, что существует некоторая латентная переменная, с помощью которой можно объяснить наблюдаемое сходство полученных оценок. Такую латентную переменную называют фактором. Данный фактор влияет на многочисленные показатели других переменных, что приводит нас к возможности и необходимости выделить его как наиболее общий, более высокого порядка. Для выявления наиболее значимых факторов и, как следствие, факторной структуры, наиболее оправданно применять метод главных компонентов (МГК). Суть данного метода состоит в замене коррелированных компонентов некоррелированными факторами. Другой важной характеристикой метода является возможность ограничиться наиболее информативными главными компонентами и исключить остальные из анализа, что упрощает интерпретацию результатов. Понятие латентности означает неявность характеристик, раскрываемых при помощи методов факторного анализа. Вначале мы имеем дело с набором элементарных признаков Xj, их взаимодействие предполагает наличие определенных причин, особенных условий, т.е. существование некоторых скрытых факторов. Последние устанавливаются в результате обобщения элементарных признаков и выступают как интегрированные характеристики, или признаки, но более высокого уровня. Естественно, что коррелировать могут не только тривиальные признаки Xj, но и сами наблюдаемые объекты Ni поэтому поиск латентных факторов теоретически возможен как по признаковым, так и по объектным данным. Гипотетически легко представить следствием такого анализа, скажем, выявление классифицирующих факторов: Fl - промышленность, F2 - сельское хозяйство и т. п.
16. Динамические системы в экономике. Возникновения хаоса в динамических системах на примере логистического дискретного отображения. Динамическая система — математическая абстракция, предназначенная для описания и изучения эволюции систем во времени. Динамическая система также может быть представлена как система, обладающая состоянием. При таком подходе, динамическая система описывает (в целом) динамику некоторого процесса, а именно: процесс перехода системы из одного состояния в другое. Фазовое пространство системы — совокупность всех допустимых состояний динамической системы. Таким образом, динамическая система характеризуется своим начальным состоянием и законом, по которому система переходит из начального состояние в другое. Динамическая система часто описывается автономной системой дифференциальных уравнений, заданной в некоторой области и удовлетворяющей там условиям теоремы существования и единственности решения дифференциального уравнения. Основное содержание теории динамических систем — это исследование кривых, определяемых дифференциальными уравнениями. Сюда входит разбиение фазового пространства на траектории и исследование предельного поведения этих траекторий: поиск и классификация положений равновесия, выделение притягивающих (аттракторы) и отталкивающих (репеллеры) множеств (многообразий). Важнейшие понятие теории динамических систем — это устойчивость (способность системы сколь угодно долго оставаться около положения равновесия или на заданном многообразии) и грубость (сохранение свойств при малых изменениях структуры динамической системы; «грубая система — это такая, качественный характер движений которой не меняется при достаточно малом изменении параметров»). Примеры экономических динамических систем: 1. Динамика банковского вклада (зависимость величины накопленных процентов по вкладу от времени); 2. Модель активного инвестора – такого инвестора, который реинвестирует (заново вкладывает исходную сумму и наращенные по ней проценты) во вклады и другие финансовые инструменты; 3. Динамическое бюджетное ограничение потребителя – бюджет потребителя складывается из изменяющихся величин (изменяется зарплата, доходы от инвестиций, расходы на инвестирование и накопление); 4. Паутинообразная модель рыночного равновесия – объем спроса в любой текущий момент времени зависит от уровня цены этого периода Pt, а предложение реагирует на изменение цены с некоторым запаздыванием и зависит от уровня цены в предшествующей периоде Pt-1. Нелинейная система — динамическая система, в которой протекают процессы, описываемые нелинейными дифференциальными уравнениями. Теория хаоса — математический аппарат, описывающий поведение некоторых нелинейных динамических систем, подверженных при определённых условиях явлению, известному как хаос (динамический хаос, детерминированый хаос). Поведение такой системы кажется случайным, даже если модель, описывающая систему, является детерминированной. Причиной появления хаоса является неустойчивость (чувствительность) по отношению к начальным условиям и параметрам: малое изменение начального условия со временем приводит к сколь угодно большим изменениям динамики системы. Примерами подобных систем являются атмосфера, турбулентные потоки, некоторые виды аритмий сердца, биологические популяции,общество как система коммуникаций и его подсистемы: экономические, политические и другие социальные системы Логистическое отображение (также квадратичное отображение) — это полиномиальное отображение, которое описывает, как меняется численность популяции с течением времени. Его часто приводят в пример того, как из очень простых нелинейных уравнений может возникать сложное, хаотическое поведение. Логистическое отображение отражает тот факт, что прирост популяции происходит в дискретные моменты времени. Математическая формулировка отображения xn +1 = rxn (1- xn) где: xn принимает значения от 0 до 1 и отражает численность популяции в n-ом году, а x0 обозначает начальную численность (в год номер 0);r — положительный параметр, характеризующий скорость размножения (роста) популяции. Это нелинейное отображение описывает два эффекта: - с одной стороны, когда численность популяции мала, она размножается со скоростью, пропорциональной этой численности; - с другой стороны, поскольку популяция обитает в среде с ограниченной «ёмкостью», то при росте плотности популяции скорость размножения падает, возрастает конкуренция и смертность.
Исследование экономических процессов с помощью многомерных нелинейных отображений, характеризующих динамику макроэкономических переменных, приводит к заключению, что этим процессам присущи, в зависимости от значений параметров, многообразные динамические режимы: равновесие, цикличность и достаточно сложное квазистохастическое поведение (детерминированный хаос). При относительно небольших значениях коэффициентов реакций цены и ставки процента на дисбаланс между спросом на товары и их предложением, а также коэффициентов реакции экономики на несоответствие спроса и предложения, система в перспективе ведет себя просто: со временем устанавливается либо равновесие, либо периодические колебания с малым периодом. Однако при увеличении даже одного из коэффициентов реакции происходит усложнение динамики переменных модели. Это означает, что в общем случае равновесное решение неустойчиво, а динамика переменных обобщенной макроэкономической модели может быть достаточно сложной и при некоторых значениях параметров приобретать стохастические свойства. Следует отметить, что сложный характер решений не следствие внешнего случайного воздействия, а внутреннее свойство используемой детерминированной модели.
Пример Найдите собственные числа и собственные векторы матрицы Решение. Составляем характеристическую матрицу Решим характеристическое уравнение (Находим корни трехчлена) для собственного вектора получаем матричное уравнение Множество собственных векторов и нулевой вектор принадлежащих одному собственному значению образуют подпространство, которое называется собственным.
А) Эконометрические модели с коррелирующими ошибками При наличии автокорреляционных взаимосвязей в ряду ошибки ковариационная матрица формально может быть представлена в виде:
Можно воспользоваться следующим практическим подходом к оценке недиагональной ковариационной матрицы ошибок эконометрической модели, отражающей существование корреляционной зависимости между ее значениями. Этот подход не требует предварительной информации относительно характера взаимосвязей между ее последовательными значениями 1) на основании исходных данных – вектора у и матрицы Х – формируется уравнение эконометрической модели, затем с помощью МНК оцениваются ее параметры, определяется вектор фактической ошибки е, значения которого проверяют с помощью критериев (например, Дарбина – Уотсона) на наличие автокорреляции. В том случае, если факт корреляции установлен, то на основе эмпирического ряда ошибки 2) определенную таким образом ковариационную матрицу фактической ошибки Процедура построения модели завершается, если критерий Дарбина – Уотсона не подтверждает наличие автокорреляции в ряду ошибок очередного этапа оценивания модели. На практике чаще всего достаточно произвести одну итерацию. Б) Эконометрические модели с гетероскедастичными ошибками В случае гетероскедастичности ошибок ковариационная матрица имеет вид:
Для эконометрических моделей с гетероскедастичными ошибками может быть применена процедура последовательных этапов расчетов, как и в случае автокорреляции между ошибками модели. Для этого на первом этапе по результатам применения обыкновенного МНК должны быть сформированы оценки При таком предположении оценки дисперсий Подобная процедура может быть реализована при любых правдоподобных гипотезах о закономерности изменения дисперсии ошибок, например, для квадратичной закономерности, для логарифмической зависимости и т.д.
Модели бинарного выбора Рассмотрим модель бинарного выбора на примере покупки семьей недвижимости. Будем считать, что зависимая переменная у = 1, если в течение исследуемого периода времени семья приобрела недвижимость, и у = 0 в противном случае. На решение о покупке недвижимости влияют самые различные факторы: доход семьи, количество ее членов, их возраст и др. Набор этих характеристик можно представить вектором Линейная модель вероятности Рассмотрим обычную линейную модель регрессии: Данная модель называется линейной моделью вероятности. Отметим некоторые особенности этой модели, которые не позволяют успешно применять МНК для оценивания коэффициентов β: 1. Ошибка ε в каждом наблюдении может принимать только два значения 2. Найдем дисперсию ошибки: 3. Прогнозные значения Эти обстоятельства существенно ограничивают область применимости линейной модели вероятности. Ее целесообразно использовать при большом числе наблюдений и при достаточно точной спецификации модели, а также как инструмент первичной обработки данных. Пробит- и логит-модели Описание модели Основной недостаток модели (1) в предположении о линейной зависимости вероятности
В частности, в качестве F (z) можно взять функцию распределения некоторой случайной величины. Одна из возможных интерпретаций модели (2) выглядит следующим образом. Предположим, что существует некоторая количественная переменная
|
|||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.92.209 (0.091 с.) |
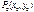 называется точкой экстремума (максимума или минимума) функции
называется точкой экстремума (максимума или минимума) функции 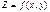 , если
, если  есть соответственно наибольшее или наименьшее значение функции
есть соответственно наибольшее или наименьшее значение функции  в некоторой окрестности точки
в некоторой окрестности точки 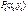
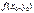 называется экстремальным значением функции (соответственно максимальным или минимальным). Говорят также, что функция
называется экстремальным значением функции (соответственно максимальным или минимальным). Говорят также, что функция 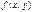 имеет в точке
имеет в точке 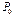 экстремума).
экстремума).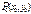 дифференцируемая функция
дифференцируемая функция 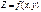 имеет экстремум, то ее частные производные в этой точке равны нулю:,
имеет экстремум, то ее частные производные в этой точке равны нулю:, 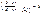
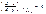 .
.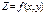 нужно приравнять нулю обе ее частные производные
нужно приравнять нулю обе ее частные производные 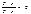 ,
, 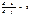 . и решить полученную систему двух уравнений с двумя неизвестными.
. и решить полученную систему двух уравнений с двумя неизвестными.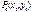 является стационарной точкой функции
является стационарной точкой функции 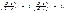 Вычислим в точке
Вычислим в точке 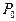 значение вторых частных производных функции
значение вторых частных производных функции  и обозначим их для краткости буквами A, B и C:
и обозначим их для краткости буквами A, B и C: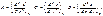
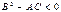 , то функция
, то функция 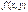 имеет в точке
имеет в точке 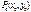 экстремум: при A <0 и C <0 и минимум при A >0 и C >0 (из условия
экстремум: при A <0 и C <0 и минимум при A >0 и C >0 (из условия 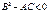 следует, что A и C обязательно имеют одинаковые знаки).
следует, что A и C обязательно имеют одинаковые знаки).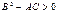 , то точка
, то точка 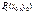 не является точкой экстремума. Если
не является точкой экстремума. Если 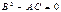 , то неясно, является ли точка
, то неясно, является ли точка 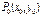 точкой экстремума и требуется дополнительное исследование.
точкой экстремума и требуется дополнительное исследование.
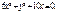
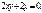 Из второго уравнения следует, что или у=0 или х=-1. Подставляя по очереди эти значения в первое уравнение, найдем четыре стационарные точки:
Из второго уравнения следует, что или у=0 или х=-1. Подставляя по очереди эти значения в первое уравнение, найдем четыре стационарные точки: 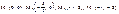 Вторые частные производные данной функции равны
Вторые частные производные данной функции равны 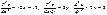 В точке М1 имеем: A =10, B =0, C =2. Здесь
В точке М1 имеем: A =10, B =0, C =2. Здесь 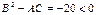 ; значит, точка М1 является точкой экстремума, и так как A и C положительны, то этот экстремум - минимум. В точке М2 соответственно будет A =-20, B =0, C =-4/3. Это точка максимума. Точки М3 и М4 не являются экстремумами функции (т.к. в них
; значит, точка М1 является точкой экстремума, и так как A и C положительны, то этот экстремум - минимум. В точке М2 соответственно будет A =-20, B =0, C =-4/3. Это точка максимума. Точки М3 и М4 не являются экстремумами функции (т.к. в них 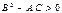 ).
).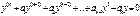 , гдеak – постоянные вещественные числа
, гдеak – постоянные вещественные числа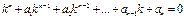 , которое получается заменой в нём производных искомой функции соответствующими степенями k, сама функция заменяется на единицу. Тогда общее решение строится в зависимости от характера корней:
, которое получается заменой в нём производных искомой функции соответствующими степенями k, сама функция заменяется на единицу. Тогда общее решение строится в зависимости от характера корней: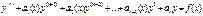

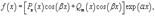 где Pn(x) и Qm(x) − многочлены степени n и m, соответственно.
где Pn(x) и Qm(x) − многочлены степени n и m, соответственно.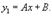
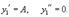
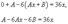



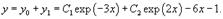
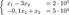 Решение: 500 000 т угля и 100 000 т стали.
Решение: 500 000 т угля и 100 000 т стали.
 : Находим характеристический многочлен (определитель характеристической матрицы)
: Находим характеристический многочлен (определитель характеристической матрицы) 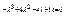
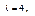
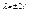 . Возьмем первый корень =4.
. Возьмем первый корень =4.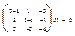 что соответствует системе уравнений
что соответствует системе уравнений 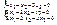 Получаем значение координат собственного вектора, соответствующего собственному числу 4:
Получаем значение координат собственного вектора, соответствующего собственному числу 4: 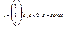
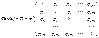
 . Согласно этому подходу матрица Cov (e) рассматривается как оценка ковариационной матрицы истинной ошибки модели Cov (ε), находится эмпирическим путем в несколько этапов:
. Согласно этому подходу матрица Cov (e) рассматривается как оценка ковариационной матрицы истинной ошибки модели Cov (ε), находится эмпирическим путем в несколько этапов: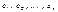 оцениваются элементы ее ковариационной матрицы по формуле
оцениваются элементы ее ковариационной матрицы по формуле 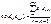 , k =1, 2,…
, k =1, 2,…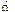 используют для оценки параметров той же модели с помощью ОМНК (формула (4)). Далее вычисляется новый ряд фактической ошибки, происходит проверка на наличие автокорреляции и, в случае подтверждения этой гипотезы, определяется новая матрица
используют для оценки параметров той же модели с помощью ОМНК (формула (4)). Далее вычисляется новый ряд фактической ошибки, происходит проверка на наличие автокорреляции и, в случае подтверждения этой гипотезы, определяется новая матрица 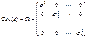
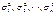 матрицы Cov (e). Сделать это на основе значений фактической ошибки
матрицы Cov (e). Сделать это на основе значений фактической ошибки 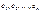 для каждой точки t = 1, 2,…, n невозможно. Вследствие этого приходится привлекать некоторые дополнительные гипотезы относительно характера изменения дисперсии ошибки, например, гипотезу о линейном законе ее изменения.
для каждой точки t = 1, 2,…, n невозможно. Вследствие этого приходится привлекать некоторые дополнительные гипотезы относительно характера изменения дисперсии ошибки, например, гипотезу о линейном законе ее изменения.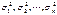 могут быть определены следующим образом. Для двух непересекающихся интервалов
могут быть определены следующим образом. Для двух непересекающихся интервалов 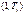 и
и 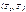 по значениям фактических ошибок
по значениям фактических ошибок 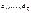 и
и 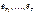 могут быть получены оценки дисперсий
могут быть получены оценки дисперсий 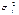 и
и 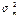 , которые соотносятся с моментами t = l и t = m, являющимися серединами этих рядов. Далее на основе этих двух значений строится линейная зависимость
, которые соотносятся с моментами t = l и t = m, являющимися серединами этих рядов. Далее на основе этих двух значений строится линейная зависимость 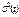 , аппроксимирующая изменение дисперсии на интервале (1, T). Каждое из найденных значений
, аппроксимирующая изменение дисперсии на интервале (1, T). Каждое из найденных значений 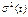 будет представлять собой оценку соответствующего элемента диагональной матрицы Ω. Эта матрица затем используется на втором этапе вычислений оценок параметров модели при помощи ОМНК.
будет представлять собой оценку соответствующего элемента диагональной матрицы Ω. Эта матрица затем используется на втором этапе вычислений оценок параметров модели при помощи ОМНК.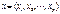 независимых переменных. Также будем предполагать, что на решение семьи влияют также неучтенные случайные факторы (ошибки). Выдвигая различные предположения о характере зависимости у от х, будем получать разные модели. Рассмотрим линейную модель вероятности, probit -модель и logit -модель.
независимых переменных. Также будем предполагать, что на решение семьи влияют также неучтенные случайные факторы (ошибки). Выдвигая различные предположения о характере зависимости у от х, будем получать разные модели. Рассмотрим линейную модель вероятности, probit -модель и logit -модель.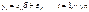 ,где t – номер наблюдения (семьи),
,где t – номер наблюдения (семьи), 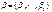 – набор неизвестных параметров (коэффициентов),
– набор неизвестных параметров (коэффициентов), 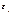 – случайная ошибка. Так как
– случайная ошибка. Так как 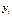 принимает значения 0 или 1 и
принимает значения 0 или 1 и 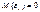 , то
, то 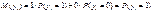 . С другой стороны, по принципам регрессионного анализа
. С другой стороны, по принципам регрессионного анализа 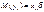 . Таким образом, линейная регрессионная модель может быть записана в виде:
. Таким образом, линейная регрессионная модель может быть записана в виде: 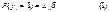
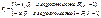 Это не позволяет считать ошибку нормально распределенной или имеющей распределение, близкое к нормальному.
Это не позволяет считать ошибку нормально распределенной или имеющей распределение, близкое к нормальному.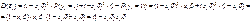 Следовательно, дисперсия ошибки зависит от
Следовательно, дисперсия ошибки зависит от 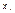 , т.е. модель гетероскедастична. Как известно, оценки коэффициентов β, полученные обычным МНК, в этом случае не являются эффективными, и желательно пользоваться обобщенным МНК.
, т.е. модель гетероскедастична. Как известно, оценки коэффициентов β, полученные обычным МНК, в этом случае не являются эффективными, и желательно пользоваться обобщенным МНК.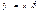 , которые по смыслу модели есть прогнозные значения вероятности
, которые по смыслу модели есть прогнозные значения вероятности 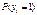 , могут лежать вне отрезка [0,1] (
, могут лежать вне отрезка [0,1] (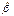 – оценка коэффициентов β, полученная с помощью обычного или обобщенного МНК), что, конечно же, не поддается разумной интерпретации.
– оценка коэффициентов β, полученная с помощью обычного или обобщенного МНК), что, конечно же, не поддается разумной интерпретации.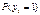 от β. Его можно преодолеть, если считать, что
от β. Его можно преодолеть, если считать, что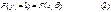 где F (z) – некоторая функция, удовлетворяющая условиям:
где F (z) – некоторая функция, удовлетворяющая условиям: 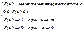
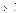 , связанная с независимыми переменными
, связанная с независимыми переменными 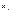 обычным регрессионным уравнением
обычным регрессионным уравнением 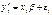 , где ошибки
, где ошибки 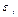 независимы и одинаково распределены с нулевым средним и дисперсией
независимы и одинаково распределены с нулевым средним и дисперсией 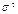 . Пусть также F (z) – функция распределения нормированной случайной ошибки
. Пусть также F (z) – функция распределения нормированной случайной ошибки 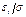 . Величина
. Величина 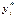 является ненаблюдаемой (латентной), а решение, соответствующее значению
является ненаблюдаемой (латентной), а решение, соответствующее значению 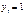 , принимается тогда, когда
, принимается тогда, когда 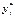 превосходит некоторое пороговое значение. Так, в примере с покупкой недвижимости можно считать, что
превосходит некоторое пороговое значение. Так, в примере с покупкой недвижимости можно считать, что 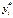 представляет собой накопления семьи с номером t. Если константа включена в число регрессоров, можно считать это пороговое значение равным нулю. Таким образом,
представляет собой накопления семьи с номером t. Если константа включена в число регрессоров, можно считать это пороговое значение равным нулю. Таким образом, 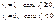 Тогда, предполагая, что случайные ошибки
Тогда, предполагая, что случайные ошибки 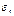 имеют одно и тоже симметричное распределение F (z) (т.е.
имеют одно и тоже симметричное распределение F (z) (т.е.