Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование выражений содержащих квадратный трехчлен.
Среди интегралов, вычисляемых методом непосредственного интегрирования, рассматривают интегралы содержащие квадратный трехчлен, то есть интегралы вида: 1) 2) Правило вычисление интегралов вида 1) 1) Выделить полного квадрат в знаменателе: :
2) Свести преобразованный интеграл к одному из табличных интегралов 11-14,учитывая,что Рассмотрим, как это сделать на примерах. Пример 2.5. Вычислить интеграл: а) б) Решение. а) Выделяя полный квадрат, в знаменателе
б)Выделяя полный квадрат, в знаменателе и применяя (в таблице основных интегралов) формулу 11, имеем:
в)Для того, чтобы свести данный интеграл к табличному виду
Правило вычисления интегралов вида 1) Находим производную знаменателя:
2) Строим в числителе производную знаменателя:
2) Разбиваем интеграл на сумму двух интегралов:
первый из них путем внесения числителя под знак дифференциала сводится к табличному интегралу
Пример 2.6. Вычислить интеграл: а) Решение. а) Находим производную знаменателя:
В числителе строим производную знаменателя:
Разбиваем преобразованный интеграл на сумму двух:
б) 1) Находим производную знаменателя:
2)В числителе строим производную знаменателя:
3) Разбиваем преобразованный интеграл на сумму двух интегралов:
в) Немного преобразуем подынтегральную функцию (вынесем 2 в знаменателе за знак интеграла - 4 под корнем):
и учитывая, что
2.2. Метод замены переменной (метод подстановки). При нахождении многих интегралов оказывается эффективной следующая идея: вместо исходной переменной
Пусть требуется вычислить интеграл
Итак, Формула (2.1) так же называется формулой замены переменной. Замечание: Если интеграл имеет вид
Запишем алгоритм действий при использовании метода замены переменной. Алгоритм (замены переменной): 1) Связать старую переменную интегрирования
2)Найти связь между дифференциалами
3) Перейти к новой переменной 4)Проинтегрировать и вернуться к старой переменной Для удобства замену далее будем писать в прямых скобках Пример 2.7. Вычислить интеграл: а) б)
Решение. а) Вводим новую переменную и избавляемся от иррациональности: Продифференцировав обе части равенства
Переходим в исходном интеграле к новой переменной Интегрируем и возвращаемся к старой переменной. Таким образом, получим:
б)
Данный пример можно решить иначе - методом подведения функции под знак дифференциала,внося
Принципиальной разницы нет, но с точки зрения оформления задания метод введения нового аргумента гораздо короче;
в)
Замечание: 1) Метод подведения функции под знак дифференциала не универсален (не всегда работает), так как в некоторых случаях невозможно подвести функцию под знак дифференциала или внесение функции под дифференциал не приводит исходный интеграл к табличному виду, в этом смысле метод замены предпочтительней; 2) Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается с практикой.
2.3. Метод интегрирование по частям. Еще один метод сведения некоторых интегралов к табличному виду. Метод основан на известной формуле производной произведения
или в дифференциальной форме Проинтегрировав обе части последнего равенства, получим
Откуда, получим формулу
Формула (2.2) называется формулой интегрирования по частям. Данная формула показывает, что нахождение интеграла При применении формулы интегрирования по частям используют следующее правило. Правило интегрирования по частям: За Рассмотрим основные виды интегралов, интегрируемых по частям: 1)
2)
Здесь
Пример 2.8. Вычислить интеграл: а) б) Решение. а)Чтобы привести интеграл к табличному виду применяем метод интегрирование по частям.Так как
б)Здесь
в)
Замечание: Формулу интегрирования по частям можно применять неоднократно. Рассмотрим, как это сделать на следующем примере. в) Применяя, формулу интегрирования по частям дважды, имеем:
Иногда повторное интегрирование по частям приводит к исходному интегралу, такие интегралы называются круговыми или циклическими интегралами. Примерами круговых интегралов являются интегралы вида
Пример 2.9. Вычислить интеграл Решение.
В результате повторного интегрирования по частям функцию не удалось привести к табличному виду. Однако последний интеграл ничем не отличается от исходного:
Замечание: Как мы видим вычисление интегралов требует индивидуального подхода к каждой подынтегральной функции, соответствующие навыки приобретаются в результате значительного числа упражнений. Задания для самостоятельного решения 1. Методом разложением на алгебраическую сумму вычислить интегралы:
Ответы: 1.1. 1.3. 1.5. 1.19. 2. Методом подведением функции под знак дифференциала вычислить интегралы:
Ответы: 2.1. 2.3. 2.5. 2.16. 2.20. 2.22. 3.Вычислить интегралы от выражений содержащих квадратный трехчлен:
Ответы: 3.1. 3.3. 3.5. 3.14. 3.22. 4.Вычислить интегралы от выражений содержащих квадратных трехчлен:
Ответы: 4.1. 4.26. 5.Найти интегралы методом замены переменной:
Ответы: 5.1. 5.3. 5.5. 6.Найти интегралы, используя формулу интегрирование по частям:
Ответы: 6.1. 6.26.
ГЛАВА 3. Методы интегрирования различных классов функций Рассмотрим методы интегрирования различных классов функций: дробно-рациональных, иррациональных, тригонометрических функций. Интегралы от данных функций сводятся к табличным соответствующей подстановкой для данного типа подынтегрального выражения. 3.1. Интегрирование рациональных функций. Дробно-рациональной функций (рациональной дробью) называется функция, равная отношению двух многочленов, то есть функция вида
где Рациональная дробь называется правильной, если Например, дробь
дробь
Как мы узнаем далее всякую правильную рациональную дробь можно представить в виде суммы конечного числа так называемых простейших рациональных дробей- этоправильные рациональные дроби следующих четырех типов: 1)
| Поделиться:
| |
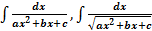 ;
;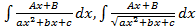 .
.
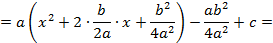
 ;
;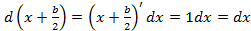 .
.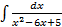 ;
;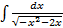 ; в)
; в) 
 и применяя (в таблице основных интегралов) формулу 14,учитывая,что
и применяя (в таблице основных интегралов) формулу 14,учитывая,что  имеем:
имеем:
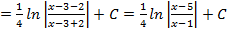 ;
; ,
,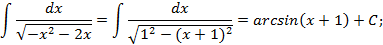
 ,достаточно вынести
,достаточно вынести  за знак интеграла
за знак интеграла  под корнем в знаменателе). Таким образом, получим:
под корнем в знаменателе). Таким образом, получим:
 .
. :
: ;
;



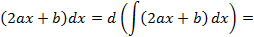


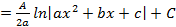 , каким образом вычисляется второй интеграл мы уже знаем (см. выше). Складывая полученные при интегрировании результаты получим ответ.
, каким образом вычисляется второй интеграл мы уже знаем (см. выше). Складывая полученные при интегрировании результаты получим ответ.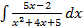 ;б)
;б) 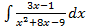 ; в)
; в)  .
. ;
; ;
;
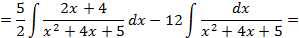

 ;
;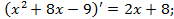
 ;
;





 , а далее применим аналогичный алгоритм решения
, а далее применим аналогичный алгоритм решения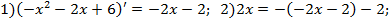
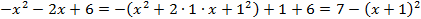 имеем:
имеем:

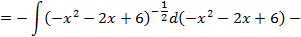


 .
. вводят новую переменную по формуле
вводят новую переменную по формуле  или
или 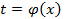 (в зависимости от вида подынтегральной функции),относительно которой исходный интеграл, являлся бы табличным или сводящимся к табличному (в случае «удачной» подстановки).Далее вычисляют этот преобразованный интеграл, а затем возвращаются к старой переменной.
(в зависимости от вида подынтегральной функции),относительно которой исходный интеграл, являлся бы табличным или сводящимся к табличному (в случае «удачной» подстановки).Далее вычисляют этот преобразованный интеграл, а затем возвращаются к старой переменной.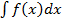 .Сделаем подстановку (замену)
.Сделаем подстановку (замену)  - некоторая функция, имеющая непрерывную производную, тогда
- некоторая функция, имеющая непрерывную производную, тогда  и согласно свойству инвариантности неопределенного интеграла получим формулу интегрирования подстановкой(заменой):
и согласно свойству инвариантности неопределенного интеграла получим формулу интегрирования подстановкой(заменой):
 (2.1)
(2.1)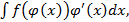 то целесообразнос делать подстановку
то целесообразнос делать подстановку  тогда
тогда  ,отсюда
,отсюда где
где 
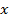 с новой переменной
с новой переменной 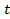 с помощью замены
с помощью замены ;
;
 ;
; .
. ;
; в)
в)  ..
.. ,
,  ;
;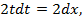 откуда
откуда  ;
;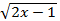 на
на  а
а  на
на 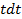 ;
;
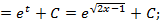

 ;
;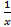 и под знак дифференциала:
и под знак дифференциала: 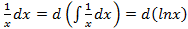 ,тогда
,тогда




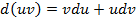 .
. , а в соответствии с приведенными выше свойствами неопределенного интеграла имеем:
, а в соответствии с приведенными выше свойствами неопределенного интеграла имеем: .
.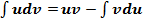 (2. 2)
(2. 2) приводит к нахождению интеграла
приводит к нахождению интеграла  ,который окажется табличным или сводящимся к табличному, в отличии от интеграла
,который окажется табличным или сводящимся к табличному, в отличии от интеграла 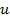 берем ту часть подынтегрального выражения, которая при дифференцировании упростится, за
берем ту часть подынтегрального выражения, которая при дифференцировании упростится, за  интеграл от которой табличный или может быть приведен к табличному.
интеграл от которой табличный или может быть приведен к табличному.

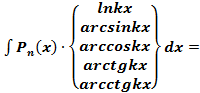

 – многочлен от
– многочлен от  ,где
,где 
 ;
; ;в)
;в)  г)
г) 
 ,следовательно за
,следовательно за  оставшуюся часть, то есть
оставшуюся часть, то есть  ,вычисляя
,вычисляя 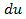 и
и  получим:
получим: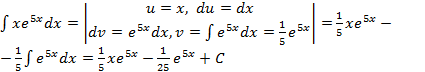 ;
; не табличный, тогда:
не табличный, тогда: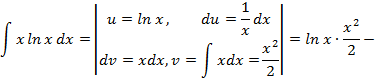
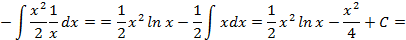
 ;
;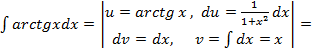
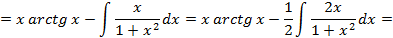
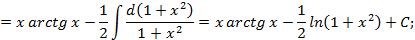

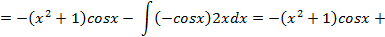

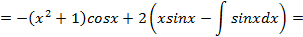
 .
.
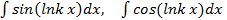 и так далее. Рассмотрим как они вычисляются.
и так далее. Рассмотрим как они вычисляются. .
.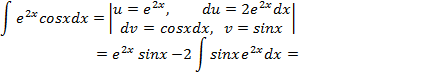

 .
. ;
;

 2.
2.  3.
3.  4.
4. 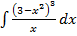 5.
5.  6.
6. 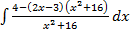 7.
7.  8.
8. 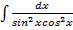 9.
9. 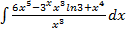 10.
10.  11.
11.  12.
12. 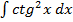 13.
13. 
 15.
15. 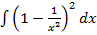 16.
16.  17.
17.  18.
18.  19.
19. 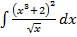 20.
20.  21.
21.  22.
22.  23.
23.  24.
24.  25.
25.  26.
26. 
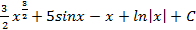 ; 1.2.
; 1.2. 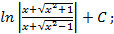
 ; 1.4.
; 1.4. 
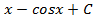 ; 1.6.
; 1.6. 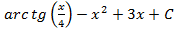 ; 1.7.
; 1.7. 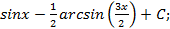 1.8.
1.8. 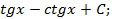 1.9.
1.9. 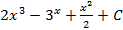 ; 1.10.
; 1.10.  ; 1.11.
; 1.11. 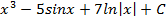 ; 1.12.
; 1.12. 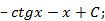 1.13.
1.13. 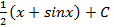 ; 1.14.
; 1.14. 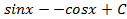 ; 1.15.
; 1.15. 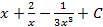 ; 1.16.
; 1.16. 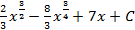 ; 1.17.
; 1.17. 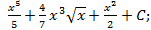 1.18.
1.18. 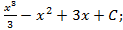
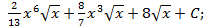 1.20.
1.20. 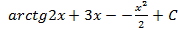 ; 1.21.
; 1.21.  ; 1.22.
; 1.22.  1.23.
1.23. 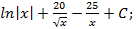 1.24.
1.24.  1.25.
1.25. 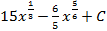 ; 1.26.
; 1.26. 
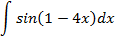
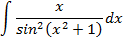


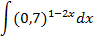
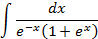
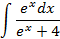

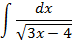
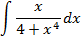
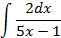
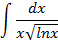

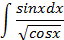
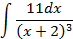
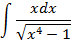
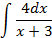
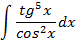
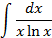
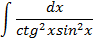
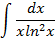
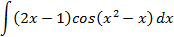
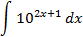
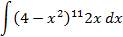
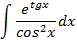

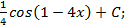 2.2.
2.2. 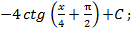
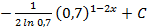 ; 2.4.
; 2.4. 
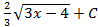 ; 2.6.
; 2.6. 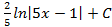 ; 2.7.
; 2.7. 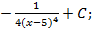 2.8.
2.8. 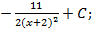 2.9.
2.9. 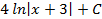 ; 2.10.
; 2.10.  2.11.
2.11. 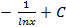 ; 2.12.
; 2.12. 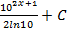 ; 2.13.
; 2.13. 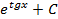 ; 2.14.
; 2.14.  ; 2.15.
; 2.15. 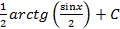 ;
;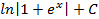 ; 2.17.
; 2.17. 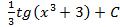 ; 2.18.
; 2.18. 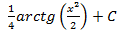 ; 2.19.
; 2.19. 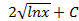 ;
;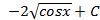 ; 2.21.
; 2.21. 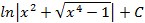 ;
;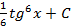 ; 2.23.
; 2.23. 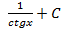 ; 2.24.
; 2.24.  ; 2.25.
; 2.25. 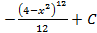 ; 2.26.
; 2.26. 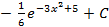 .
.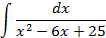
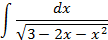
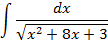
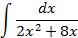
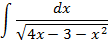

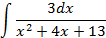

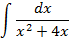

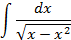
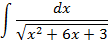

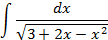



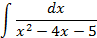

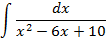

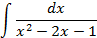
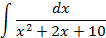
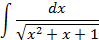
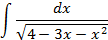
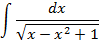
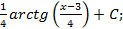 3.2.
3.2. 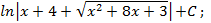
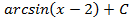 ; 3.4.
; 3.4. 
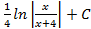 ; 3.6
; 3.6 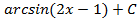 ; 3.7.
; 3.7. 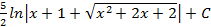 ; 3.8.
; 3.8. 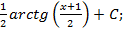 3.9.
3.9. 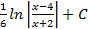 ; 3.10.
; 3.10. 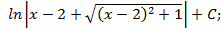 3.11.
3.11.  ; 3.12.
; 3.12. 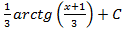 ; 3.13.
; 3.13. 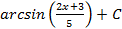 ;
; ; 3.15.
; 3.15.  ; 3.16.
; 3.16. 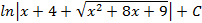 ; 3.17.
; 3.17. 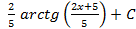 ; 3.18.
; 3.18. 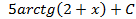 ; 3.19.
; 3.19. 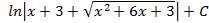 ; 3.20.
; 3.20.  3.21.
3.21. 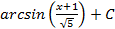 ;
; ; 3.23.
; 3.23. 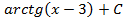 ; 3.24.
; 3.24. 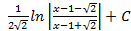 ; 3.25.
; 3.25.  ; 3.26.
; 3.26.  .
.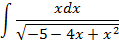
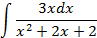
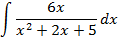
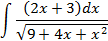
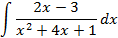
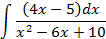
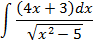
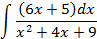

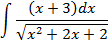
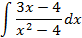
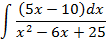
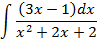

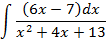
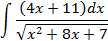
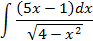




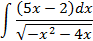
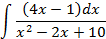
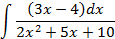
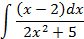

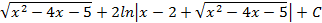 ; 4.2.
; 4.2. 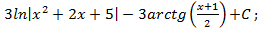 4.3.
4.3.  ; 4.4.
; 4.4.  4.5.
4.5. 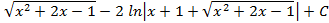 ; 4.6
; 4.6 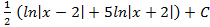 ; 4.7.
; 4.7.  ; 4.8.
; 4.8. 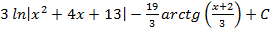 ; 4.9.
; 4.9. 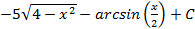 ; 4.10.
; 4.10. 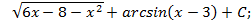 4.11.
4.11. 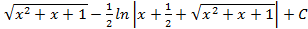 ; 4.12.
; 4.12. 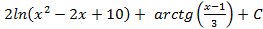 ; 4.13.
; 4.13.  ; 4.14.
; 4.14. 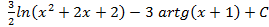 ; 4.15.
; 4.15.  4.16.
4.16. 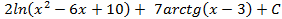 ; 4.17.
; 4.17. 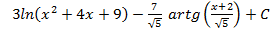 ; 4.18.
; 4.18. 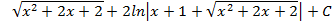 ; 4.19.
; 4.19. 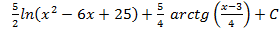 ; 4.20.
; 4.20. 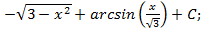 4.21.
4.21. 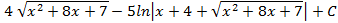 ; 4.22.
; 4.22. 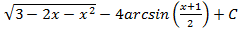 ; 4.23.
; 4.23. 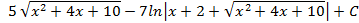 ; 4.24.
; 4.24. 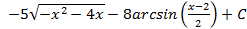 ; 4.25.
; 4.25. 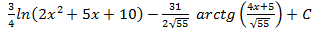 ;
;
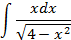
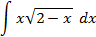
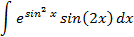
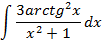
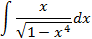
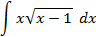

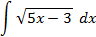
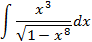
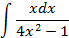
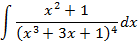
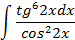
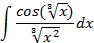
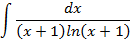
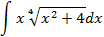
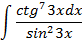
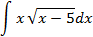


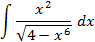
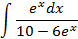
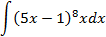
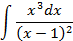
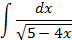
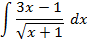
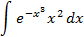
 5.2.
5.2. 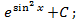
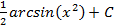 ; 5.4.
; 5.4. 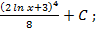
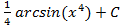 ; 5.6.
; 5.6. 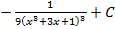 ; 5.7.
; 5.7. 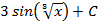 ; 5.8.
; 5.8. 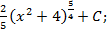 5.9.
5.9.  5.10.
5.10.  5.11.
5.11. 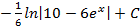 ; 5.12.
; 5.12.  ; 5.13.
; 5.13. 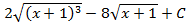 ; 5.14.
; 5.14. 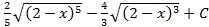 ; 5.15.
; 5.15.  ; 5.16.
; 5.16. 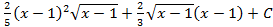 ; 5.17.
; 5.17. 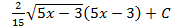 ; 5.18.
; 5.18. 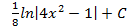 ; 5.19.
; 5.19. 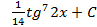 ; 5.20.
; 5.20. 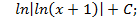 5.21.
5.21. 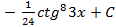 ; 5.22.
; 5.22. 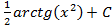 ; 5.23.
; 5.23. 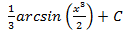 ; 5.24.
; 5.24.  ; 5.25.
; 5.25. 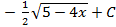 ; 5.26.
; 5.26. 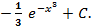
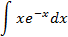

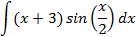
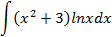
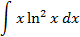

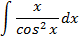
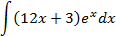
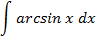
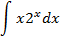
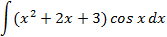

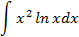
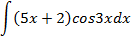

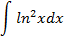
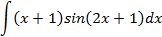
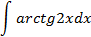
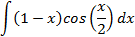
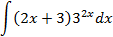

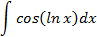

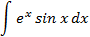
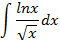

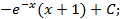 6.2.
6.2. 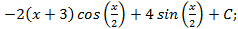 6.3.
6.3. 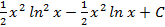 ; 6.4.
; 6.4. 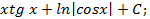 6.5.
6.5.  ; 6.6
; 6.6 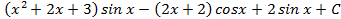 ; 6.7.
; 6.7.  ; 6.8.
; 6.8. 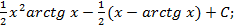 6.9.
6.9.  6.10.
6.10. 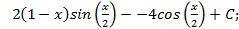 6.11.
6.11. 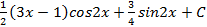 ; 6.12.
; 6.12. 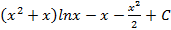 ; 6.13.
; 6.13. 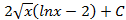 ; 6.14.
; 6.14.  ; 6.15.
; 6.15.  ; 6.16.
; 6.16. 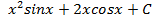 ; 6.17.
; 6.17.  ; 6.18
; 6.18  ; 6.19.
; 6.19. 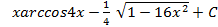 ; 6.20.
; 6.20. 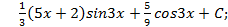 6.21.
6.21. 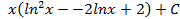 ; 6.22.
; 6.22.  ; 6.23.
; 6.23.  ; 6.24.
; 6.24.  ; 6.25.
; 6.25.  ;
;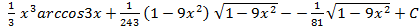 .
. (3.1),
(3.1),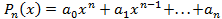 ,
,  многочлены от переменной
многочлены от переменной 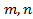 соответственно,
соответственно, 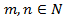 -натуральные числа.
-натуральные числа.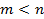 и неправильной, если
и неправильной, если  .
.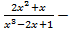 правильная, так как
правильная, так как  ,где
,где  ,
,  ;
;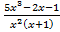 неправильная, так как
неправильная, так как 
 ,
, 
 .
.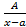 ;2)
;2)  ;3)
;3)