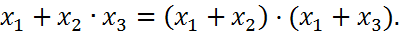Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Существенные и несущественные переменные .
Булева функция y=f(x1,x2,…,xn) существенно зависит от переменной xk, если существует такой набор значений a 1, a 2,…, a k-1, a k+1, a k+2,…, an, что f(a1,a2,…,ak-1, 0, ak+1,ak+2,…,an) ≠ ≠ f(a1,a2,…,ak-1, 1, ak+1,ak+2,…,an). В этом случае xk называют существенной переменной, в противном случае xk называют несущественной (фиктивной) переменной. Другими словами, переменная является несущественной, если ее изменение не изменяет значения функции.
Пример 1.4.1. Пусть булевы функции f1(x1,x2) и f2(x1,x2) заданы следующей таблицей истинности:
Для этих функций переменная x1 — существенная, а переменная x2—несущественная. Очевидно, что булевы функции не изменяют свои значения путем введения (или удаления) несущественных переменных. Поэтому, в дальнейшем булевы функции рассматриваются с точностью до несущественных переменных (в примере можно записать: f1(x1,x2)=x1, f2(x1,x2)=x1).
§1.5. Таблицы истинности. Эквивалентные функции. Зная таблицы истинности для элементарных функций, можно вычислить таблицу истинности той функции, которую реализует данная формула. Пример 1.5.1. F1=x1˄x2˅(x1˄x2˅x1˄x2 )
Таким образом, формула F1 реализует дизъюнкцию.
Пример 1.5.2. F2=x1˄x2→x1
Пример 1.5.3. F3=((x1˄x2)⊕x1)⊕x2.
Таким образом, формула F3 реализует дизъюнкцию.
Булевы функции f1 и f2 называются эквивалентными, если на всяком наборе (a 1, a 2,…, an) нулей и единиц значения функций совпадают. Обозначение эквивалентных функций следующее: f1=f2. Согласно приведенным примерам 1-3, можно написать • x1˄x2˅(x1˄x2˅x1˄x2 ) = x1˄x2; • x1˄x2→x1 =1; • ((x1˄x2)⊕x1)⊕x2=x1˅x2.
§1.6. Аксиоматика и основные законы алгебры логики. Прежде всего остановимся на рассмотрении аксиом булевой алгебры.
1. Аксиомы, утверждающие, что в булевой алгебре рассматриваются только двоичные переменные:
х=0, если х х=1, если х 2. Аксиомы, определяющие логические операции И и ИЛИ: 0 1+1=1; 1+0=0+1=1; 0+0=0.
3. Аксиомы, определяющие операцию логического отрицания:
4. Аксиома симметричности: если
5. Аксиома транзитивности: если
6. Аксиома рефлексивности: х= х.
Аксиомы 4, 5, 6 формулируют свойства отношения эквивалентности. Из этих свойств следует принцип подстановки: если
Перейдем к рассмотрению основных законов булевой алгебры. С помощью аксиом булевой алгебры можно доказать целый ряд законов методом перебора всех значений логических переменных. Основные законы алгебры логики принято разбивать на три группы.
1. Законы одинарных элементов. а) Законы универсального множества: б) Законы нулевого множества:
2. Законы отрицания. а) Закон двойного отрицания: б) Законы дополнительности: в)Законы двойственности (де-Моргана):
3. Комбинационные законы. а) Законы тавтологии (идемпотентности): Отсюда следует, что булева алгебра является алгеброй без степенией и коэффициэнтов. б) Переместительные законы (коммутативные):
в) Сочетательные законы (ассоциативные):
г) Распределительные законы (дистрибутивные). Распределительный закон первого рода (умножение относительно сложения): Распределительный закон второго рода (сложение относительно умножения):
Для проверки истинности приведенных эквивалентностей достаточно построить соответствующие таблицы истинности.
Отметим, что в обычной алгебре не действуют законы тавтологии и распределительный закон второго рода.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 157; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.247.188 (0.016 с.) |
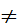 1;
1;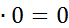 ; 0
; 0 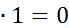 ; 1
; 1 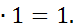
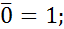

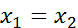 , то
, то 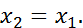
 и
и  , то
, то 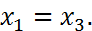
 , то в любом логическом выражении, содержащем
, то в любом логическом выражении, содержащем 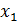 , вместо
, вместо  и в результате будет получено эквивалентное логическое выражение.
и в результате будет получено эквивалентное логическое выражение.
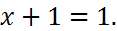


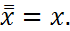

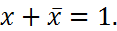
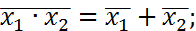
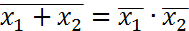 .
.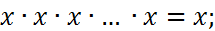

 ;
; 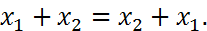
 ;
;