Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кластеризация. Выбор метрики
Пусть имеется r -мерная выборка Типовые метрики:
Еще рассматривают:
В ИМС MatLab имеется функция pdist.m, которая возвращает попарные расстояния между объектами: Y =pdist(X,’metric’). Возможности выбора метрики зависят от используемой версии ИМС (см. help pdist). Функция squareform(Y) преобразует этот набор Y в матрицу попарных расстояний. Вариант ввода исходных данных и построения матрицы попарных расстояний приведен в Документе 8.1, результат вычислений – на рис. 8.1.
Clear; clc; X=[3 1.7; 1 1; 2 3; 2 2.5; 1.2 1; 1.1 1.5; 3 1 ]; Y=pdist(X,'euclid'); W = squareform (Y); Disp('Матрица попарных расстояний:'); Disp(W); | ||||||
| Матрица попарных расстояний: 0 2.1190 1.6401 1.2806 1.9313 1.9105 0.7000 2.1190 0 2.2361 1.8028 0.2000 0.5099 2.0000 1.6401 2.2361 0 0.5000 2.1541 1.7493 2.2361 1.2806 1.8028 0.5000 0 1.7000 1.3454 1.8028 1.9313 0.2000 2.1541 1.7000 0 0.5099 1.8000 1.9105 0.5099 1.7493 1.3454 0.5099 0 1.9647 0.7000 2.0000 2.2361 1.8028 1.8000 1.9647 0 |
Рис.8.1. Экранный вывод в примере 8.1
8.2. Метод k средних и ЕМ -алгоритм
1) n исходных объектов выбирается k объектов, которые объявляются центрами классов. Их можно выбирать различными способами:
|
|
- Случайным образом,
- Выбирать самые далекие друг от друга объекты,
- Брать пары объектов, дальше всего разнесенные друг от друга по разным координатным осям и т.п.
2) Сканируется весь набор исходных объектов: очередной объект присоединяется к j -му классу, если его расстояние до центра этого класса минимально.
3) Определяются новые центры сформированных классов и сканирование повторяется заново.
Процесс останавливается либо когда стабилизируются центры классов, либо после заданного числа итераций. Такой подход называют алгоритмом Мак-Кина.
Вместо расстояния до центра можно использовать среднее арифметическое (или медиана) расстояний до всех объектов класса. Такой подход называют методом динамических сгущений.
Присоединение очередного объекта к j -му классу корректирует его центр и ковариационную матрицу. Эта корректировка осуществляется по известным рекуррентным формулам
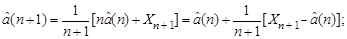
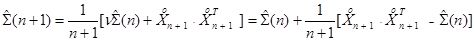
Начальные условия имеют вид 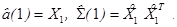 Каждый объект присоединяется к тому классу, который после этой корректировки оказывается наиболее компактным: контролируется либо максимальное расстояние между элементами этого нового класса, либо максимальное собственное число матрицы
Каждый объект присоединяется к тому классу, который после этой корректировки оказывается наиболее компактным: контролируется либо максимальное расстояние между элементами этого нового класса, либо максимальное собственное число матрицы 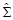 , либо ее определитель и т.п. Этот алгоритм можно интерпретировать как вычисление апостериорных вероятностей принадлежности объекта тому или иному классу и выбор класса с наибольшей апостериорной вероятностью. Для этого подхода разработана эффективная численная реализация – EM-алгоритм.
, либо ее определитель и т.п. Этот алгоритм можно интерпретировать как вычисление апостериорных вероятностей принадлежности объекта тому или иному классу и выбор класса с наибольшей апостериорной вероятностью. Для этого подхода разработана эффективная численная реализация – EM-алгоритм.
В Документе 8.2 сформирована 2-мерная выборка, содержащая 3 класса, и приведены варианты обращения к нескольким стандартным функциям ИМС MatLab, на рис.8.2 - экранный вывод для метода k средних.
| Документ 8.2. Выделение K кластеров |
| clear; clc; %Формирование 3 классов a =4; n 1=50; n 2=30; n 3=40; X1=randn(n1,2); X1(:,1)=-a+X1(:,1); X1(:,2)=a+X1(:,2); X2=randn(n2,2); X2(:,1)= a+X2(:,1); X2(:,2)=a+X2(:,2); X3=randn(n3,2); X3(:,1)= X3(:,1); X3(:,2)=-a+X3(:,2); X 0=[ X 1; X 2; X 3]; K =3; % Задание числа кластеров Y=pdist(X0,'Euclid'); Z=linkage(Y,'single'); % dendrogram (Z); %построение дерева разбиений (дендрограммы) %T=cluster(Z,K); %разбиение на K классов T=kmeans(X0,3,'distance','sqEuclidean'); % метод k средних subplot(1,2,1); plot(X1(:,1),X1(:,2),'*','LineWidth',2); grid; hold on; plot(X2(:,1),X2(:,2),'or','LineWidth',2); hold on; plot(X3(:,1),X3(:,2),'sg','LineWidth',2); for k=1:K; I=find(T==k); Z=X0(I,:); if length(I)>2; Q=convhull(Z(:,1),Z(:,2)); hold on; plot(Z(Q,1),Z(Q,2),'k','LineWidth',2); else hold on; plot(Z(:,1),Z(:,2),'dk','LineWidth',3); end; end; subplot(1,2,2); silhouette(X0,T); |
|
|
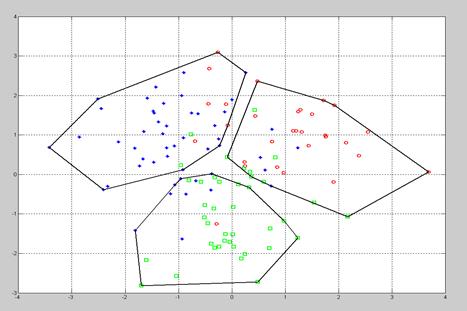
Рис. 8.2. Результат вычислений в Документе 8.2
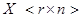 : i -й столбец матрицы X, i = 1,…, n представляет собой результаты измерений r признаков i -го объекта, представленные (тем или иным способом) в виде безразмерных величин. Задача состоит в разделении выборки на k компактных классов так, чтобы в некоторой метрике расстояния между элементами каждого класса были малы по сравнению с расстояниями между классами. Если число классов заранее не известно, задачу приходится решать в интерактивном режиме.
: i -й столбец матрицы X, i = 1,…, n представляет собой результаты измерений r признаков i -го объекта, представленные (тем или иным способом) в виде безразмерных величин. Задача состоит в разделении выборки на k компактных классов так, чтобы в некоторой метрике расстояния между элементами каждого класса были малы по сравнению с расстояниями между классами. Если число классов заранее не известно, задачу приходится решать в интерактивном режиме.