Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Игры, повторяемые многократно. Смешанные стратегии
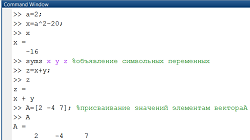
Если партнеры играют только один раз, то игрокам целесообразно придерживаться принципа минимакса, как в игре с седловой точкой, так и в игре без седловой точки. В случае многократного повторения игры с седловой точкой игрокам также целесообразно придерживаться принципа минимакса. Если же многократно повторяется игра без седловой точки, то постоянное использование минимаксных стратегий становится невыгодным. Действительно, в игре без седловой точки элемент платежной матрицы Более того, доказано, что при многократно повторяемой игре без седловой точки, игроку А, для обеспечения среднего выигрыша большего чем По этой причине для многократно повторяемых игр без седловой точки вводится понятие смешанной стратегии. В играх, которые повторяются многократно, каждая из стратегий Смешанной стратегией Смешенные стратегии игрока А записываются в в виде матрицы
или в виде строки Аналогично определяются и обозначаются смешанные стратегии
З а м е ч а н и е. Чистые стратегии можно считать частным случаем смешенных и задавать строкой, в которой 1 соответствует чистой стратегии. Смешанные стратегии, избранные игроками, называются оптимальными, если одностороннее отклонение любым игроком от своей оптимальной стратегии может изменить средний выигрыш только в сторону невыгодную для игрока.
Совокупность, состоящая из оптимальной стратегии одного игрока и оптимальной стратегии другого игрока, называется оптимальным решением или решениемигры. Средний выигрыш В 1928 году фон Нейманом была доказана основная теорема теории игр, утверждающая, что каждая конечная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий. Поскольку все чистые стратегии являются частными случаями смешенных стратегий, то из основной теоремы теории игр можно получить: следствие 1. Любая игра имеет цену; следствие 2. Цена игрыудовлетворяет неравенству Стратегии, входящие в оптимальную стратегию с отличной от нуля вероятностью, называются активными. Справедлива теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то средний выигрыш остается неизменным и равным цене игры Эта теорема имеет большое практическое значение, так как указывает методы нахождения оптимальных стратегий при отсутствии седловой точки. 1.4. Аналитический метод решения игры размера 2 Рассмотрим игру размера 2
Такая игра является простейшим случаем конечной игры. Если она имеет седловую точку, то оптимальное решение – это пара чистых стратегий, соответствующих этой точке. Игра, в которой отсутствует седловая точка, в соответствии с основной теоремой теории игр, имеет оптимальное решение, которое определяется парой смешанных стратегий Для того чтобы их найти воспользуемся теоремой об активных стратегиях. Если игрок А придерживается своей оптимальной стратегии
Средний выигрыш игрока А, если он использует оптимальную смешанную стратегию
Тот же средний выигрыш получит игрок А, если второй игрок применяет стратегию Решив эту систему линейных алгебраических уравнений методом Крамера, получим оптимальную стратегию
и цену игры Аналогичным образом можно найти оптимальную стратегию
которой имеет вид:
1.5. Графический метод решения игр 2 Рассмотрим игру размера 2
и проведем через точку (1; 0) координатной плоскости Оху прямую l, перпендикулярную оси абсцисс. После этого для каждой из стратегий соединяющую точку (0; Если игрок А применяет смешанную стратегию
и этому выигрышу соответствует точка М на прямой
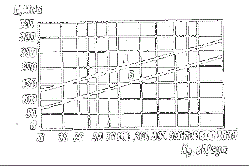
Рис. 1.2
Ломаная
Рис. 1.3 Далее, непосредственно по чертежу, находим пару активных стратегий игрока В, пересекающихся в точке N (если в точке N пересекается более двух стратегий, то выбираем любые две из них). Пусть это будут стратегии Вероятности
игрока В определяются из соотношения
З а м е ч а н и е. Иногда точка не является пересечением двух стратегий, а попадает на одну из прямых х = 0 или х = 1. В этом случае решением игры будут соответствующие чистые стратегии.
Для игры размера m
БИМАТРИЧНЫЕ ИГРЫ 2.1 Бескоалиционные биматричные игры в нормальной форме Рассматривается конечная бескоалиционная игра двух лиц с ненулевой суммой, которая называется биматричной игрой. Это неантагонистическая игра, формализующая конфликтную ситуацию, в которой интересы сторон (игроков) не являются противоположными.
В играх такого рода при одинаковых совокупностях стратегий игроки получают различные выигрыши. Игра может быть представлена двумя матрицами одинаковых размерностей. Это матрица А (таблица 2.1) и матрица В (таблица 2.2) выигрышей, соответственно, первого и второго игроков.
Т а б л и ц а 2.1 Матрица А - матрица выигрышей первого игрока
Строки этих матриц ставятся во взаимно однозначное соответствие стратегиям Каждый элемент первой матрицы В биматричных играх, в отличие от игр с нулевой сумой, конфликт интересов участников игры может быть не таким острым, как в матричных, Т а б л и ц а 2.2 Матрица В - матрица выигрышей второго игрока
поскольку здесь выигрыш одного из игроков сопровождается в общем случае не равным по величине проигрышем другого игрока.
Снижение остроты конфликта, а так же участие в игре достаточно большого числа игроков создают благоприятные условия для создания коалиций и коопераций, то есть согласованного взаимодействия отдельных участников игры. Однако в данном разделе рассматриваются бескоалиционныебиматричные игры в нормальной форме. Рассмотрим примеры биматричных игр. Одной из наиболее известных является так называемая «Дилемма заключенных», для которой существует несколько различных вариантов. П р и м е р 2.1. «Дилемма заключенных» "Игроками" являются двое заключенных, обвиняемых в совершении тяжелого преступления. Каждый из них располагает двумя стратегиями:
сознаваться ( В игре возможны следующие ситуации: – оба сознаются (набор стратегий – оба не сознаются ( – если первый сознается, а второй нет ( – если сознается второй, а первый нет ( Здесь В качестве значений платежных матриц берутся сроки заключения с обратными знаками. Игра задается платежными матрицами первого и второго игроков:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.199.188 (0.07 с.) |
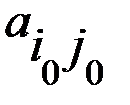 , соответствующий минимаксной стратегии игрока А, не обязан быть минимальным в своей строке. Следовательно, игрок В, зная о том, что игрок А в следующей игре будет использовать минимаксную стратегию
, соответствующий минимаксной стратегии игрока А, не обязан быть минимальным в своей строке. Следовательно, игрок В, зная о том, что игрок А в следующей игре будет использовать минимаксную стратегию 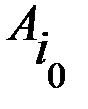 , может выбрать стратегию, отвечающую минимальному элементу строки
, может выбрать стратегию, отвечающую минимальному элементу строки  . В результате выигрыш игрока А уменьшится от величины
. В результате выигрыш игрока А уменьшится от величины 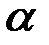 . Аналогично может поступить и игрок А, неожиданно применив против игрока В стратегию, соответствующую максимальному элементу столбца
. Аналогично может поступить и игрок А, неожиданно применив против игрока В стратегию, соответствующую максимальному элементу столбца  .
. ,
, 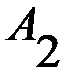 ,
, 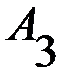 , …,
, …,  . Игроку В для улучшения результата также целесообразно чередовать свои стратегии
. Игроку В для улучшения результата также целесообразно чередовать свои стратегии 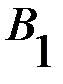 ,
,  ,
, 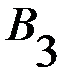 , …,
, …, 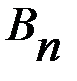 .
. игрока А называется применение чистых стратегий
игрока А называется применение чистых стратегий  ,
, 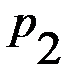 ,
,  , …,
, …,  , причем сумма вероятностей равна 1 (
, причем сумма вероятностей равна 1 (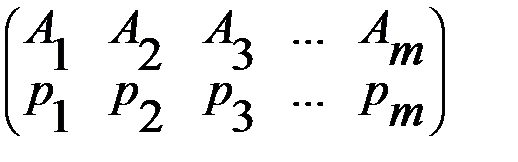
 .
. игрока В:
игрока В: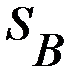 =
=  или
или 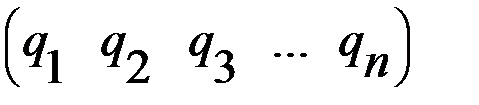 , где сумма вероятностей появления стратегий равна 1 (
, где сумма вероятностей появления стратегий равна 1 ( +
+  +
+  +…+
+…+ 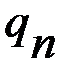 = 1).
= 1). при применении обоими игроками оптимальных стратегий называется ценой игры.
при применении обоими игроками оптимальных стратегий называется ценой игры.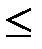
 .
. 2
2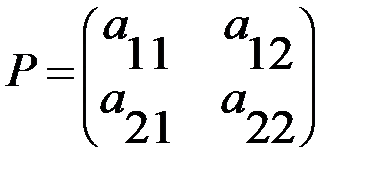 .
. и
и 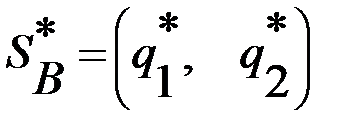 .
.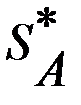 , то его средний выигрыш будет равен цене игры
, то его средний выигрыш будет равен цене игры 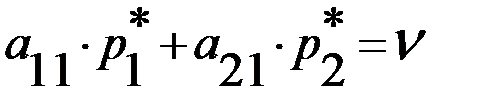 .
. . Учитывая, что
. Учитывая, что 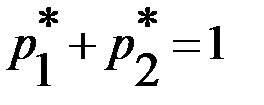 , получаем систему уравнений для определения оптимальной стратегии
, получаем систему уравнений для определения оптимальной стратегии 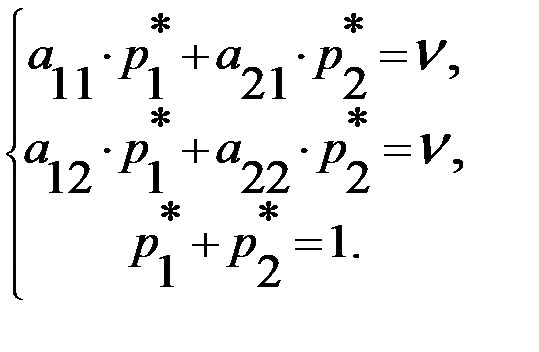



 ,
, 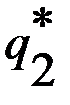 и
и 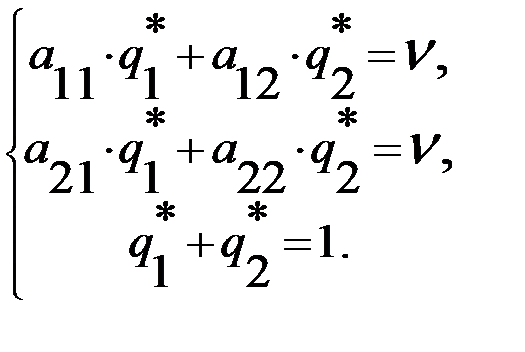 решение
решение
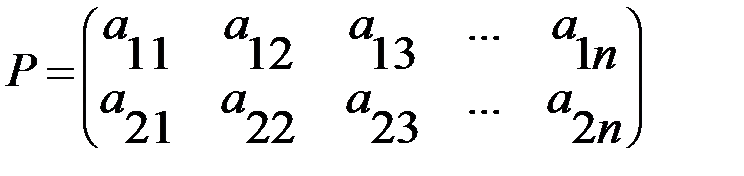
 (i = 1, 2, …, n) проведем прямую
(i = 1, 2, …, n) проведем прямую  ,
, ) на оси Оу с точкой (1;
) на оси Оу с точкой (1;  ) на прямой l. Ось Оу отвечает за стратегию
) на прямой l. Ось Оу отвечает за стратегию  , а прямая l за стратегию
, а прямая l за стратегию  .
. , то его выигрыш в случае, если противник применяет чистую стратегию
, то его выигрыш в случае, если противник применяет чистую стратегию  ,
, c абсциссой
c абсциссой 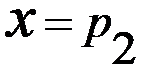 (рис. 1.2).
(рис. 1.2).
 , отмеченная на чертеже (рис. 1.3) жирной линией, позволяет определить минимальный выигрыш игрока А при любом поведении игрока В. Точка N, в которой эта ломанная достигает максимума, определяет решение и цену игры. Ордината точки N равна цене игры
, отмеченная на чертеже (рис. 1.3) жирной линией, позволяет определить минимальный выигрыш игрока А при любом поведении игрока В. Точка N, в которой эта ломанная достигает максимума, определяет решение и цену игры. Ордината точки N равна цене игры 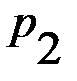 – вероятности применения стратегии
– вероятности применения стратегии 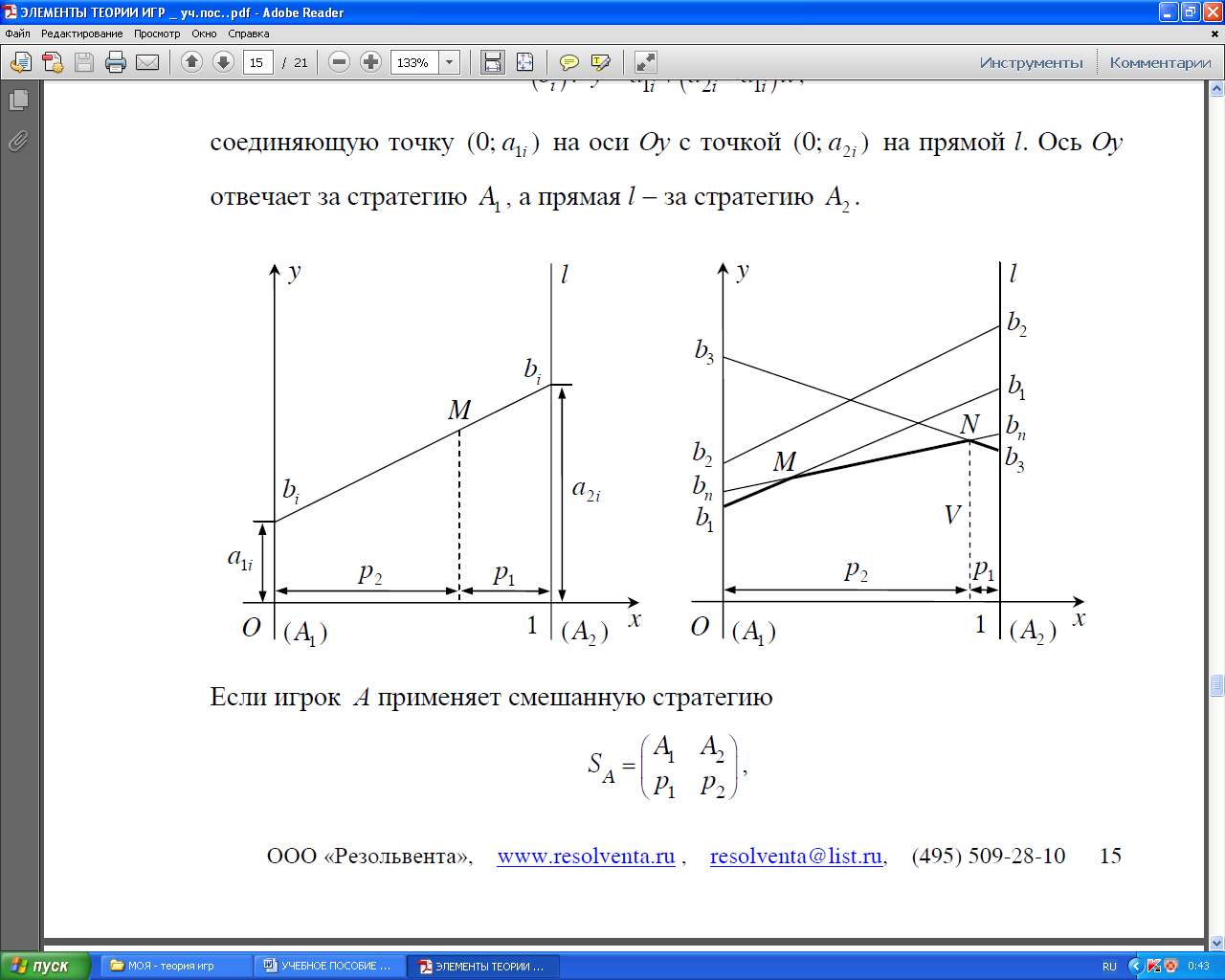
 . Поскольку выигрыш игрока А, если он придерживается оптимальной стратегии, не зависит от того, с какими вероятностями игрок В применяет эти стратегии, то неизвестные
. Поскольку выигрыш игрока А, если он придерживается оптимальной стратегии, не зависит от того, с какими вероятностями игрок В применяет эти стратегии, то неизвестные  ,
,  и
и 



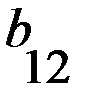
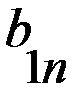

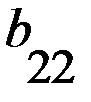
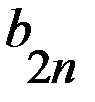
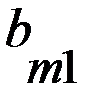
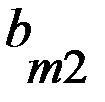
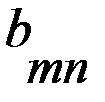
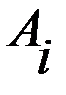 первого игрока, а столбцы
первого игрока, а столбцы 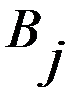 стратегиям второго игрока.
стратегиям второго игрока. 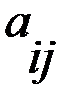 представляет численное значение выигрышей первого игрока при стратегиях
представляет численное значение выигрышей первого игрока при стратегиях  , а каждый элемент второй матрицы
, а каждый элемент второй матрицы 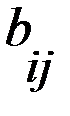 представляет численное значение выигрышей второго игрока в аналогичных ситуациях.
представляет численное значение выигрышей второго игрока в аналогичных ситуациях.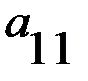
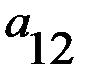


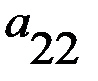
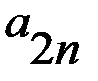
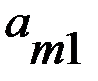
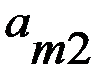
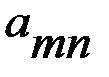
 лет заключения (большой срок, но не максимальный);
лет заключения (большой срок, но не максимальный);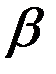 лет за менее тяжкие преступления, в которых они уже уличены;
лет за менее тяжкие преступления, в которых они уже уличены;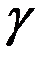 лет, а второй получает максимальный срок в
лет, а второй получает максимальный срок в  лет;
лет;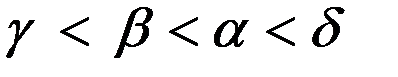 .
. ,
, 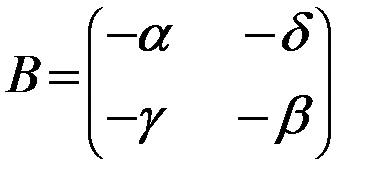 .
.