
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2. Задачи раскраски графовСодержание книги Поиск на нашем сайте Хроматическое число графа Во введении приводился пример задачи раскраски карты, при которой никакая пара соседних стран не была бы окрашена в один цвет. Эту задачу нетрудно свести к задаче на графов. Для этого сопоставим каждой стране вершину графа и соединим пары вершин рёбрами, если соответствующие страны имеют общую границу. Таким образом, приходим к следующей задаче: необходимо раскрасить вершины графа различными цветами так, чтобы никакое ребро графа не соединяло вершин одного цвета. Соответствующие раскраски называются допустимыми (правильными). Вершинная раскраска некорректна для графов, содержащих петли. Ясно также, что наличие кратных ребер не влияет на раскраску. Поэтому в задачах раскраски не ограничивая общности будем рассматривать простые (обыкновенные) графы, не содержащие петель и кратных ребер. Если задача не содержит никаких дополнительных ограничений, то она имеет тривиальное решение: достаточно раскрасить каждую вершину в свой уникальный цвет. Поэтому обычно накладываются ограничения на число используемых цветов. Граф G называется k -раскрашиваемым, если для построения допустимой раскраски вершин графа G достаточно использования k цветов. Если граф G является k -раскрашиваемым, но не является (k -1)- раскрашиваемым, то он называется k -хроматическим, а само число k называется хроматическим числом. Для хроматического числа графа G будем использовать обозначение c (G). Рассмотрим классы графов, обладающих заданным хроматического числа. Нетрудно видеть, что класс 1-хроматических графов (с c (G)=1) – класс пустых графов (не содержащих рёбер). Описание класса 2-хроматических графов дает следующая теорема. Теорема 2.1.1. Граф G является 2-хроматическим тогда и только тогда, когда он не содержит циклов нечётной длины. Доказательство. Выделим в графе G основное дерево. Очевидно, что его можно раскрасить допустимым образом в два цвета (например, красить по слоям). При этом вершины дерева, соединяемые цепью чётной длины, будут иметь одинаковые цвета, а вершины, соединяемые цепью нечётной длины, - разные цвета. Необходимость. Пусть граф G допускает правильную раскраску в два цвета, тогда и любое его остовное дерево будет окрашено в два цвета. Если бы в графе G были циклы нечетной длины, то концевые вершины каждого добавляемого ребра, порождающего цикл нечётной длины, были бы окрашены в один цвет, так как они соединяются в дереве цепью чётной длины, Приходим к противоречию, поскольку нам дано, что граф G допускает правильную раскраску в два цвета. Достаточность. Если граф G не содержит циклов нечётной длины, то допустимая раскраска любого его островного дерева будет допустимой раскраской и всего графа G, так как добавляемые к остову рёбра, порождающие циклы четной длины, будут соединять вершины, удаленные в остовном дереве на нечётное расстояние и, следовательно, окрашенные в различные цвета. ð В качестве примера 2-хроматичских графов можно привести класс двудольных графов Для класса 3-хроматичских графов до сих пор не получено описания на уровне необходимого и достаточного условия. О хроматическом числе произвольного графа G мало, что можно сказать. Ясно, что, с одной стороны, оно не превосходит n - числа вершин графа G, а с другой, не меньше r -числа вершин в максимальном полном подграфе графа G, таким образом, r £ c (G) £ n. Для получения более содержательных оценок хроматического числа необходимо располагать дополнительной информацией о графе. В качестве примера рассмотрим следующее утверждение. Теорема 2.1.2. Если наибольшая из степеней вершин графа G равна r, то граф (ρ+1) -раскрашиваемый. Доказательство проводится индукцией по N - числу вершин графа G. 1. Для N =1 утверждение очевидно, так как ρ=0 и ρ+1=1. 2. Предположим, что утверждение верно и для графов с числом вершин N =2,3, …, n. 3. Рассмотрим произвольный граф G с числом вершин N = n +1, степень каждой из которых не превосходит ρ. Удалим некоторую вершину графа вместе с инцидентными ей рёбрами. В полученном графе будет n вершин, степень каждой из которых не превосходит ρ. По предположению индукции его можно раскрасить (ρ+1) цветом. Вершины, которые были смежны с удаленной вершиной, будут окрашены не более чем в ρ цветов, даже если все они будут разноцветными. При этом ранее удаленную вершину можно раскрасить (ρ+1) -м цветом, получив допустимую раскраску всего графа. ð Эта теорема информативна для однородных графов - графов с одинаковыми степенями вершин или графов близких к однородным, позволяя получать результат близкий к хроматическому числу. 2.2. Свойства планарных графов Граф любой карты на поверхности земного шара является планарным, учитывая возможность её стереографической проекции на плоскость. Планарный граф, реализованный на плоскости, называется плоским. Для плоского графа вводится понятие грани – части плоскости, ограниченной со всех сторон рёбрами и вершинами графа.Обозначим через f число граней плоского графа. Л.Эйлером была установлена связь между числом вершин, ребер и граней в плоских графах. Теорема 2.2.1. Для числа вершин, ребер и граней связного плоского графа G справедливо равенство n + f = m + 2 (2.2.1) Доказательство проводится индукцией по M -числу рёбер графа G. 1.Для М=1 возможны 2 случая: а) одна вершина с петлей: n =1, m =1, f =2; б) две смежные вершины: n =2, m =1, f =1. В обоих случаях значения левой и правой частей выражения (2.2.1) совпадают и равны 3. 2. Предположим, что равенство (2.2.1) верно и для любого связного плоского графа с числом ребер M =2,3, …, m. 3. Покажем, что равенство (2.2.1) справедливо для любого связного плоского графа с числом ребер M = m +1. Рассмотрим все возможные способы построения связного плоского графа с числом ребер M = m +1 на основе связного плоского графа с числом ребер M = m. Добавляемое (m +1) -оеребро может быть: а) петлёй. В этом случае увеличится на 1 число граней f (новая грань расположена внутри петли) и равенство (2.2.1) сохранится. б) ребром, соединяющим две вершины, принадлежащие границе одной грани. Добавляемое ребро разобьет эту грань на две, т.е. число граней f увеличится на 1 и равенство (2.2.1) сохранится. в) ребром, соединяющим некоторую вершину исходного графа с новой вершиной. В этом случае увеличится на 1 число вершин n, число граней f останется неизменным и равенство (2.2.1) сохранится. Других способов увеличения числа ребер в плоских графах не существует. ð Формулу (2.2.1) называют еще формулой Эйлера для многогранников, поскольку она связывает число вершин, рёбер и граней выпуклых многогранников. Несмотря на относительно простое доказательство теоремы 2.2.1, формула Эйлера позволяет получать важные свойства планарных графов, на основе которых эффективно решаются задачи раскраски планарных графов. Следствие 2.2.1. Если G – простой связный планарный граф с n ≥ 3 вершинами и m рёбрами, то m ≤ 3 n – 6 (2.2.2) Доказательство. Рассмотрим плоскую укладку графа G. Введем вспомогательную величину Q (G), равную общему числу рёбер вокруг всех граней графа G. Оценим величину Q (G) сверху и снизу. Так как каждая грань простого плоского графа ограничена не менее чем тремя рёбрами, то Q (G) ³ 3 f. С другой стороны, каждое ребро может входить в границу не более двух граней, учитываясь в Q (G) не более 2 раз. Следовательно, Q (G)≤2 m. Сопоставляя оба неравенства, получаем соотношение 3 f ≤2 m. После его подстановкив формулу (2.2.1) получаем соотношение (2.2.2). ð Если выполняется равенство m =3 n – 6, то такой планарный граф называется максимальным. Границы всех граней максимального плоского графа содержат по три ребра. Используя свойства максимальных плоских графов, можно доказать, что любой планарный граф допускает плоскую укладку, в которой каждое ребро является отрезком прямой (попробуйте это доказать). Теорема 2.2.2. В любом простом планарном графе G существует вершина, степень которой не превосходит 5. Доказательство. Без потери общности можно считать граф плоским, связным и содержащим не менее трёх вершин. Предположим, что степени всех вершин графа больше или равны 6. Нетрудно видеть, что сумма степеней всех вершин графа равна 2 m, поскольку в указанной сумме каждое из m рёбер учитывается дважды. Из предположения следует, что 2 m ³ 6 n, то есть m ³ 3 n. Подставляя это соотношение в (2.2.2), приходим к противоречию 3 n ≤ 3 n -6. ð 2.3. Раскраска планарных графов Теорема 2.3.1. Любой планарный граф G с n ≥ 6 вершинами 6-раскра-шиваемый. Доказательство проводится индукцией по N - числу вершин графа G. 1. Для N =6 утверждение очевидно. 2. Предположим, что утверждение верно и для любого планарного графа с числом вершин N =7,8, …, n. 3. Пусть G – произвольный планарный граф с n +1 вершиной. Не теряя общности, можно считать G простым графом (добавление кратных рёбер не влияет на раскраску). По теореме 2.2.2 граф G содержит вершину v, степень которой не превосходит 5. Если удалить её вместе с инцидентными рёбрами, то оставшийся граф будет 6-раскрашиваемым по предположению индукции. Требуемая раскраска в 6 цветов для всего графа G получается, если окрасить вершину v цветом, отличным от цветов не более пяти смежных с ней вершин. ð Этот результат можно усилить и доказать с помощью более тщательных рассуждений возможность раскраски любого планарного графа в 5 цветов. Теорема 2.3.2. Любой планарный граф G с n ≥ 5 вершинами 5-раскра-шиваемый. Доказательство проводится индукцией по N - числу вершин графа G. 1. Для N =5 утверждение очевидно. 2. Предположим, что утверждение верно и для любого планарного графа с числом вершин N =6,7, …, n. 3. Пусть G – произвольный планарный граф с n +1 вершиной. Не теряя общности, можно считать G простым графом (добавление кратных рёбер не влияет на раскраску). По теореме 2.2.2 граф G содержит вершину v 0, степень которой не превосходит 5. Если удалить её вместе с инцидентными рёбрами, то оставшийся граф будет 5-раскрашиваемым по предположению индукции. Если степень вершины v 0 меньше 5 или если среди вершин, смежных с вершиной v 0, найдутся, по крайней мере, две с одинаковыми цветами, то для вершины v 0 среди 5 цветовнайдется свободный цвет без перекраски других вершин. Осталось рассмотреть случай, когда все вершины Если вершины v 1 и v 3 принадлежат разным компонентам связности подграфа G 1,3, то в одной из этих компонент перекрасим вершины 1-го цвета на 3-ий цвет, а вершины 3-го цвета на 1-ый цвет. После этого обе вершины v 1 и v 3 станут 1-го цвета или 3-го цвета и для вершины v 0 найдется свободный цвет среди 5 используемых цветов. Заметим, что указанная перекраска сохранит раскраску всего графа допустимо. Действительно, взаимный обмен 1-го и 3-го цветов не может привести к появлению ребер с одноцветными концевыми вершинами, как для ребер с концевыми вершинами 1-го и 3-го цветов, так и для ребер, одна из концевых вершин которых имеет цвет, отличный от 1-го и 3-го. Если вершины v 1 и v 3 принадлежат одной компоненте связности подграфа G 1,3, то в плоской укладке графа G можновыделить цикл, содержащий ребра (v 0, v 1),…,(v 3, v 0), вершины которого (кроме вершины v 0) окрашены чередующимся способом в 1-й или 3-й цвет. Внутри этого цикла находится вершина v 2, а вершина v 4 снаружи. Вершины v 2 и v 4 должны принадлежать разным компонентам связности подграфа G 2,4, поскольку в противном случае в плоской укладке графа G можнобыло бы выделить цикл, содержащий ребра (v 0, v 2),…,(v 4, v 0), вершины которого (кроме вершины v 0) окрашены чередующимся способом во 2-й или 4-й цвет. Цвет общей вершины указанных двух циклов Вершинная раскраска графов также иллюстрирует возможность существенной зависимости сложности решения задач дискретной математики от незначительного изменения параметров задачи. Так, до сих пор нет приемлемого, с традиционной точки зрения, доказательства возможности раскраски любого планарного графа в 4 цвета. Глава 3. Способы задания графов 3.1. Алгоритмические вопросы В предыдущих двух главах было рассмотрено несколько задач, в которых формулировались условия существования в графах тех или иных объектов или свойств (эйлеров цикл, цепь, раскраска в заданное число цветов). В теории графов, как и в дискретной математике в целом, значительное внимание уделяется алгоритмическим задачам, связанным с построением конкретных решающих алгоритмов, их обоснованием и оценкам сложности. Рассмотрим для примера алгоритм построения эйлерова цикла в графе, все вершины которого имеют четные степени. Доказательство теоремы 1.3.1 существования эйлерова цикла не содержит описания алгоритма его построения. К настоящему времени сформулировано несколько таких алгоритмов. Рассмотрим пошаговое описание одного из алгоритмов построения эйлерова цикла. Алгоритм построения эйлерова цикла 1. Выбрать в графе произвольную вершину а. 2. Выбрать некоторое ребро u, инцидентное вершине а. 3. Выбранное ребро занести в список ребер эйлерова цикла, перейти по нему к другой вершине, а ребро удалить из графа. 4. Находясь в некоторой вершине x, не выбирать среди инцидентных ребер те, которые соединяют вершину x с начальной вершиной а, если есть другие возможности. 5. Находясь в некоторой вершине x, не выбирать среди инцидентных ребер то, которое является мостом в оставшемся подграфе. Обоснование алгоритма 1.Покажем, что предписания алгоритма всегда выполнимы. Предположим, что в ходе реализации алгоритма достигнута некоторая вершина b. Если b ¹ a, то текущий оставшийся подграф связен (ребра-мосты не выбирались) и степени всех его вершин четны, кроме вершин a и b. По следствию 1.3.2. этот подграф содержит эйлерову цепь, соединяющую вершины b и a. Если b = a, то текущий оставшийся подграф будет эйлеровым пока не все ребра, инцидентные вершине a удалены. 2. Покажем, что предписания алгоритма приводят к построению полного эйлерова цикла, т.е., что не останется непройденных ребер. Учитывая предыдущее, после окончания работы алгоритма все ребра, инцидентные начальной вершине a, должны быть пройдены. Если непройденное ребро имеет общую вершину с ребром, инцидентным вершине a, то это означает, что на некотором этапе выполнения алгоритма было нарушено предписание п.4. Если непройденное ребро не имеет общей вершины с ребром, инцидентным вершине a, то это означает, что на некотором этапе выполнения алгоритма было нарушено предписание п.5. ð Каждый алгоритм ориентирован на некоторого конкретного исполнителя, обладающего определенными возможностями (своей системой команд). Так, например, если исполнитель не знает, как проверить, является ли ребро мостом, то в алгоритм придется добавить соответствующее разъяснение. Например, проверять, будет ли связен оставшийся подграф после удаления из него проверяемого ребра. Этот процесс детализации продолжается до тех пор, пока в предписаниях алгоритма останутся только те действия, которые исполнитель в состоянии выполнять. Задачи на графах, содержащих десятки, сотни и тысячи вершин, решаются с помощью ЭВМ, поэтому при выборе алгоритмов решения необходимо также учитывать способы задания графов. Информацию о графах можно задавать в двух основных формах: матричных и списковых. Матричные способы позволяют широко использовать при работе имеющееся программное обеспечение, однако, обладают значительной избыточностью, поскольку в них указывается не только то, что есть в графе, но и то, чего в графе нет. Для графов большой размерности это неприемлемо. Списковые представления позволяют экономить память, но требуют, обычно, дополнительного программирования. Матричные формы Ограничимся рассмотрением матриц смежности и инцидентности, наиболее часто используемых при задании графов. Матрицы смежности Для простого неориентированного графа G (V, E), ê V ê = n матрица смежности A =|| Пример 3.2.1.Матрица смежности графа, изображенного ниже, имеет следующий вид:
V 2 V 4 2 1 0 1 1 0 3 0 1 0 1 0 4 0 1 1 0 1 V 1 V 5 5 1 0 0 1 0 Из свойств матрицы смежности следует, что для восстановления обыкновенного графа G достаточно задать информацию об элементах, расположенных над (под) главной диагональю. Каждый двоичный элемент требует 1 бит памяти. Всего потребуется n (n -1)/2 бит памяти. Если граф G содержит петли и кратные ребра, то элементами
1 0 1 0 0 1 V 2 V 4 2 1 0 1 2 0 3 0 1 0 1 0 4 0 2 1 1 1 V 1 V 5 5 1 0 0 1 0 Для восстановления графа G,содержащего петли и кратные ребра необходимо добавить к элементам, расположенных над (под) главной диагональю, n элементов главной диагонали. Каждый из n (n +1)/2 элементов может содержать число, не превосходящее m, потребует é log 2 m ù бит памяти. Всего необходимо n (n +1) é log 2 m ù /2 бит памяти. Для ориентированных графов D (V, X) элемент
1 0 1 0 1 V 2 V 4 2 0 0 1 0 3 2 0 0 1 V 1 4 0 0 0 0 Отсутствие симметрии в матрице смежности ориентированного графа D (V, X) приводит к необходимости задания элементов как над, так и под главной диагональю, а при наличии дуг-петель - всех элементов матрицы смежности. Если граф D (V, X) простой, то потребуется n (n -1) бит памяти, в противном случае n 2 é log 2 m ù бит. Матрицы инцидентности Для простого неориентированного графа G (V, E), ê V ê = n матрица инцидентности B =|| Пример 3.2.2.Матрица инцидентности графа, изображенного ниже, имеет следующий вид
4 5 1 1 1 0 0 0 0 V 2 6 V 4 2 0 1 0 1 0 1 2 3 3 0 0 0 1 1 0 4 0 0 1 0 1 1 V 1 1 V 5 5 1 0 1 0 0 0 Поскольку каждый столбец матрицы инцидентности содержит по две единицы, то для однозначного восстановления обыкновенного графа G достаточно задать информацию о любых n -1 строках матрицы инцидентности. Каждый двоичный элемент требует 1 бит памяти. Всего потребуется (n -1) m бит. Если граф G содержит петли и кратные ребра, то столбцы бинарной матрицы инцидентности B могут содержать по одной единице и повторяться.
4 5 7 1 1 1 0 0 0 0 0 0 V 2 6 V 4 2 0 1 0 1 0 1 0 1 2 8 3 3 0 0 0 1 1 0 0 0 1 4 0 0 1 0 1 1 1 1 V 1 V 5 5 1 0 1 0 0 0 0 0 Для однозначного восстановления графа G, содержащего петли и кратные ребра, необходима информация обо всей матрице инцидентности, т.е. nm бит. Для ориентированных графов D (V, X) элемент
Поскольку элементы матрицы инцидентности любого ориентированного графа D принимают не более четырех различных значений, то для задания каждого элемента матрицы инцидентности необходимо по 2 бит памяти. Учитывая разнообразие элементов матрицы для ориентированных графов однозначное восстановление графа D возможно по любым (n -1) строкам матрицы инцидентности. Всего потребуется 2(n -1) m бит памяти. Списковые представления Остановимся здесь только на наиболее часто используемых списковых формах задания. Список ребер Этот способ позволяет задавать любой граф, не содержащий изолированных вершин. Простому графу G из примера 3.2.1 соответствует следующий список ребер: (v 1, v 2) (v 2, v 3) (v 3, v 4) (v 4, v 5) (v 5, v 1) (v 2, v 4). Графу с петлями и кратными ребрами из того же примерасоответствует список: (v 1, v 2) (v 2, v 3) (v 3, v 4) (v 4, v 4) (v 4, v 5) (v 5, v 1) (v 2, v 4) (v 2, v 4). Для орграфов список ребер переходит в список дуг, задаваемых упорядоченными парами вершин. В любом случае список ребер (дуг) требует 2 m é log 2 n ù бит памяти. Списки смежности Они соответствуют «отжатой от нулей» матрице смежности. Количество списков равно числу вершин графа. Список с i -м номером содержит номера вершин, смежных с i -ойвершиной. Пример 3.3.1.Простому графу из примера 3.2.1 соответствуют следующие списки смежности: 1: 2,5 2: 1,3,4 3: 2,4 4: 2,3,5 5: 1,4.
Графу с петлями и кратными ребрами из того же примерасоответствуют списки смежности: 1: 2,5 2: 1,3,4,4 3: 2,4 4: 2,2,3,5,4 5: 1,4.
Для орграфов каждый список разбивается на два подсписка: вершин на входе и вершин на выходе. В качестве разделителя используется специальный символ (например, ноль). Списки смежности для орграфа из примера 3.2.2: 1: 3,3,0,2,4 2: 1,0,3 3: 2,0,1,1,4 4: 1,3,0,4. Память компьютера имеет линейную структуру, поэтому при вводе информации в компьютер в конце каждого списка (они могут иметь разную длину) необходимо также указывать разделитель - специальный символ (например, ноль). Поскольку в списках смежности информация о каждом ребре (дуге) задается дважды, то списки смежности занимают (2 m + n) é log 2 (n +1) ù бит памяти для неориентированных графов и 2(m + n) é log 2 (n +1) ù бит памяти для ориентированных графов. Сокращенные списки смежности При использовании данного способа задания информация о каждом ребре указывается для сокращения избыточности только один раз. В каждом списке перечисляются номера только тех смежных вершины, номера которых не меньше номера списка. Для обозначения пустых списков будем использовать символ Æ. Пример 3.3.2.Обыкновенному графу из примера 3.2.1 соответствуют сокращенные списки смежности: 1: 2,5 2: 3,4 3: 4 4: 5 5: Æ.
Графу с петлями и кратными ребрами из того же примерасоответствуют сокращенные списки смежности: 1: 2,5 2: 3,4,4 3: 4 4: 5,4 5: Æ.
Сокращенные списки смежности для орграфа из примера 3.2.2: 1: 3,3,0,2,4 2: 0,3 3: 0,4 4: 0,4.
Поскольку в сокращенных списках смежности информация о каждом ребре (дуге) указывается один раз, то эти списки занимают (m + n) é log 2 (n +1) ù бит памяти для неориентированных графов и (m +2 n) é log 2 (n +1) ù бит памяти для ориентированных графов. Поскольку информация о каждом ребре задается один раз, то дальнейшее сокращение длины кода возможно лишь за счет более экономного кодирования разделителей. Рассмотрим случай неориентированных графов. На разделители отводится n é log 2 (n +1) ù бит. Если m £ n é log 2 (n +1) ù, то возможен более экономный способ задания разделителей. К записи номера каждой вершины добавляется контрольный бит, в который заносится ноль, если вершина не является последней в списке, и единица, если соответствующая вершина последняя в данном списке. Всего на разделители потребуется m бит памяти. Сокращенные списки смежности будут занимать m ( é log 2 n ù +1) бит памяти. Поскольку теперь число ноль не используется в качестве разделителя, то можно нумеровать вершины графа, начиная с нуля. Однако, не любая нумерация будет теперь допустимой. Нельзя будет воспользоваться таким нумерациями, при которых возможны пустые списки перед непустыми. Для исключения подобных ситуаций в первую очередь необходимо нумеровать вершины, у которых есть еще не занумерованные смежные вершины.
1: 2,3,4 2: 3,5 3: Æ 4: 5 5: Æ При сокращении объема памяти необходимой для записи информации о графе естественно возникает вопрос, до каких пор возможно без потерь «сжимать» информацию. Для ответа на этот вопрос необходима математическая постановка задачи.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

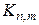 , очевидно, не содержащих циклов нечетной длины.
, очевидно, не содержащих циклов нечетной длины.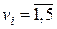 ,смежные с вершиной v 0 имеют разные цвета. Для упрощения обозначений, будем считать, что каждая вершина
,смежные с вершиной v 0 имеют разные цвета. Для упрощения обозначений, будем считать, что каждая вершина  расположены вокруг вершины v 0 в порядке её кругового обхода. Выделим в G подграф G 1,3, порожденный вершинами 1-го и 3-го цветов. Вершины v 1 и v 3 могут принадлежать, как одной компоненте связности подграфа G 1,3, так и разным компонентам.
расположены вокруг вершины v 0 в порядке её кругового обхода. Выделим в G подграф G 1,3, порожденный вершинами 1-го и 3-го цветов. Вершины v 1 и v 3 могут принадлежать, как одной компоненте связности подграфа G 1,3, так и разным компонентам.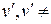 v 0 должен быть равен 1 или 3 (в подграфе G 1,3), но, с другой стороны, он должен быть равен 2 или 4 (в подграфе G 2,4) Пришли к противоречию. Таким образом, к вершинам v 2 и v 4 можно будет применить перекраску, рассмотренную в предыдущем абзаце. ð
v 0 должен быть равен 1 или 3 (в подграфе G 1,3), но, с другой стороны, он должен быть равен 2 или 4 (в подграфе G 2,4) Пришли к противоречию. Таким образом, к вершинам v 2 и v 4 можно будет применить перекраску, рассмотренную в предыдущем абзаце. ð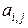 ||,
||, 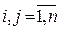 является бинарной, симметрической с элементами
является бинарной, симметрической с элементами 

 V 3 1 2 3 4 5
V 3 1 2 3 4 5 1 0 1 0 0 1
1 0 1 0 0 1
 V 3
V 3  1 2 3 4 5
1 2 3 4 5

 V 3 1 2 3 4
V 3 1 2 3 4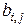 ||,
||,  ,
,  является бинарной с элементами
является бинарной с элементами 

 V 3 1 2 3 4 5 6
V 3 1 2 3 4 5 6

 V 3 1 2 3 4 5 6 7 8
V 3 1 2 3 4 5 6 7 8

 Пример 3.3.3.Для обыкновенного графа из примера 3.2.1 приведены сокращенные списки для нумерации, не являющейся допустимой
Пример 3.3.3.Для обыкновенного графа из примера 3.2.1 приведены сокращенные списки для нумерации, не являющейся допустимой


