Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
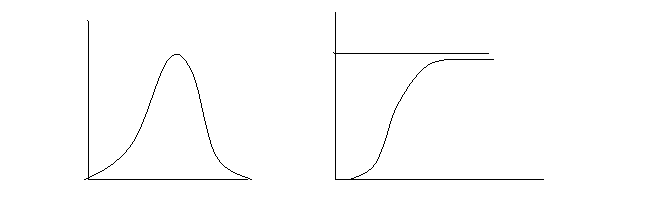
Формирование нормально распределенных случайных чисел,
На практике для нормального закона нашел применение метод, основанный на центральной предельной теореме вероятностей. По этой теореме в результате суммирования определенного числа независимых случайных величин, сравнимых по первым двум моментам распределения получается случайная величина, приближенно распределенная по нормальному закону. Если случайная величина R распределена равномерно в интервале [0, 1], то ее математическое ожидание m и дисперсия D равны:
s2= Согласно центральной предельной теореме теории вероятностей при сложении достаточно большого числа независимых случайных величин получается случайная величина, имеющая приближенно нормальное распределение. Составим сумму n независимых, распределенных равномерно в интервале [0, 1] случайных величин Rj, где j = 1, n (x) Þ Для нормирования этой суммы найдем ее матожидание m и дисперсию D. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых. Сумма содержит n слагаемых, матожидание каждого из которых равно 1/2, следовательно: M(x) ® Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых. Сумма содержит n независимых слагаемых, дисперсия каждого из которых равна 1/12, следовательно, дисперсия суммы: D (x) ® Следовательно, s= Пронормируем рассматриваемую сумму, т. е. перейдем к одной переменной:
В соответствии с центральной предельной теоремой при n ® ¥ распределение этой величины стремится к нормальному закону с параметрами М (х)=0 и s=1. При конечном n распределение приближенно нормальное. В практических задачах достаточно n =12 и получается удобное для расчета приближение. При 6-ти распределениях Симпсона (по Гаврилову) распределение приближается к нормальному.
Уже при n = 4 распределение приближается к нормальному закону.
Метод обратной функции
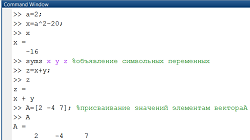
Случайная величина Х описывается интегральной F (x) и дифференциальной f (x) функциями распределения. Зная одну изэтих функций, можно предсказать поведение случайной величины, так как функции связаны между собой соотношениями:
Условие формирования непрерывной случайной величины Х по заданному закону распределения: поскольку Ri = F (х i), то необходимо выполнить преобразование
Х i = F –1(Ri),
где Ri — равномерно распределенное случайное число; F –1 – функция, обратная по отношению к распределению случайной величины Х.
Использование метода обратной функции для расчета случайной величины требует сравнительно больших затрат машинного времени, так как связано с численным решением не поддающегося аналитическому расчету интеграла. Имеются табулированные значения интеграла для нормированной величины S = (х – m x)/s x, по которым, записав таблицу в память ЭВМ можно находить случайные величины, распределенные по требуемому закону. На основании данного выражения можно моделировать случайные числа с требуемым законом распределения.
|
|||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 87; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.180.223 (0.006 с.) |
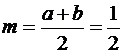
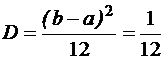 .
.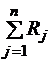 .
.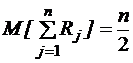
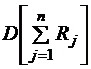 = n /12
= n /12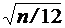 .
.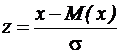 ®
® 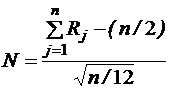
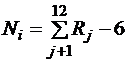 N в интервале [-3, 3]
N в интервале [-3, 3]
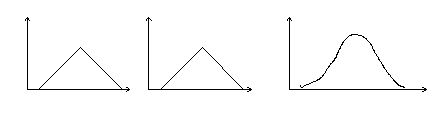
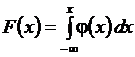 , j (x)= F ¢ (x)
, j (x)= F ¢ (x)