Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование дифференциального бинома
, (5.5) где a, b ∈ R, m, n, p ∈ Q. Как показал П. А. Чебышев, интегралы вида (5.5) «берутся» лишь в следующих случаях: 1) если p ∈ Z, используется подстановка x = yk, где k − на- именьшее общее кратное знаменателей дробей n и m; 2) S − знаменатель дроби p; 3) если = yS, где S − знаменатель дроби p. Приведем конкретные примеры:
Рассмотренный пример относится к первому случаю. Кро- ме этого для “взятия” интеграла мы использовали метод интег- рирования по частям.
В данном случае m = 5; n = 3; p = 2/3; x = (y 3 − 1)1/3;
Следовательно, получаем
, т. е. в данном случае имеем
т. е. имеем случай 3. Используем подстановку 2 − x 3 = x 3 y 3 или 2 х -3 − 1 = y 3.
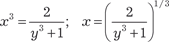 ; ;
.
Следовательно, исходный интеграл примет вид
Определенный интеграл К понятию определенного интеграла можно прийти, рас- сматривая различные задачи, например нахождение площади плоской фигуры, вычисление работы переменной силы, опре- деление пути по заданной переменной скорости.
M 1 M 2 M 3 M n - 1 M n Рис. 5.2 Разделим отрезок [ a, b ] на n частичных интервалов: [ x 0, x 1], [ x 1, x 2], …, [ x n -1, x n ]. В точках деления отрезка [ a,b ] проведем прямые, парал- лельные оси 0 y, и разобьем криволинейную трапецию aABb на n частичных трапеций. В каждом из частичных интервалов возьмем по произвольной точке М 1, М 2,…, М n (некоторые из этих точек могут совпадать с точками деления отрезка [ a, b ]).
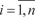 , то площадь ступенчатой фигуры можно найти по формуле , то площадь ступенчатой фигуры можно найти по формуле
(5.6)
При неограниченном увеличении количество частичных интервалов (n →) и при стремлении длины наибольшего из них к нулю ступенчатая фигура будет неограниченно прибли- жаться к криволинейной трапеции aABb, т. е. получим
Зная площадь криволинейной трапеции, мы можем нахо- дить площади любых плоских фигур (этот вопрос мы подробнее рассмотрим ниже). К выражению вида (5.7) приводят и другие задачи (нахождение работы переменной силы, вычисление пути по заданной переменной скорости). Теперь приведем строгое определение определенного ин- теграла. Впервые для непрерывной функции оно было дано в 1823 г. французским математиком Коши, а позднее немецкий матема- тик Риман показал, что определение Коши применимо к более широкому классу функций. Это позволило ему впервые дать в общей форме определение интеграла и определить условие его существования. Рассмотрим непрерывную на отрезке [ a, b ] функцию y = = f (x) (f (x) не обязательно положительна на [ a, b ]). Отрезок [ a, b ] разбивается на n частичных интервалов точками a = x 0, x 1, x 2, …, x n = b причем x 0 < x 1 < x 2 <…< x n. Во всех частичных интервалах [ x 0, x 1], [ x 1, x 2], …, [ x n -1, x n ] берутся произвольно точки М 1, М 2, …, М n, находятся значения функций y = f (x) в этих точках f (M 1), f (M 2), …, f (M n). Составляем сумму вида
где x i = x i − x i -1. (5.8) Затем находим предел интегральной суммы (5.8) при стремлении к нулю длины наибольшего частичного интервала, т. е. при max x i → 0.
В рассмотренной нами задаче о криволинейной трапеции предел (5.9) определяет ее площадь. В общем случае он называ- ется определенным интегралом от функции f (x) в пределах от a до b и читается: интеграл от a до b f (x) по dx. Таким образом, согласно определению, получаем:
Сумма в выражении (5.8) называется n -й интегральной суммой. Как и в неопределенном интеграле f (x) — есть подынтег- ральное функция, f (x) dx — подынтегральное выражение, пе- ременная х — переменная интегрирования, отрезок [ a, b ] на- зывается интервалом интегрирования, а числа а и b нижним и верхним пределами соответственно. Определенный интеграл есть некоторое число, а величина его зависит только от вида функции f (x) и от чисел а и b. Заме- тим, что площадь криволинейной трапеции — это геометричес- кий смысл определенного интеграла. Вычисление определенно- го интеграла с помощью составления интегральных сумм вида (5.8) вызывает серьезные проблемы даже в самых простых слу- чаях, поэтому для их нахождения используют другой способ, который мы рассмотрим ниже. Теперь приведем без доказательства теорему существова- ния определенного интеграла. Теорема 5.2. Если функция f (x) непрерывна в отрезке [ a,b ], то ее n -я интегральная сумма стремится к пределу при стрем- лении к нулю длины наибольшего частичного интервала. Этот предел, т. е. определенный интеграл
не зависит ни от способа разбиение [ a, b ] на частичные интерва- лы, ни от выбора в этих интервалах промежуточных точек.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.240.61 (0.015 с.) |

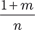 ∈ Z, то применяется подстановка (bxn + a) = yS, где
∈ Z, то применяется подстановка (bxn + a) = yS, где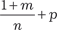 ∈ Z, то применяется подстановка a · x-n + b =
∈ Z, то применяется подстановка a · x-n + b =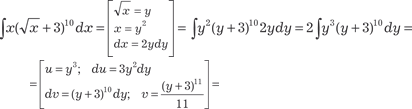
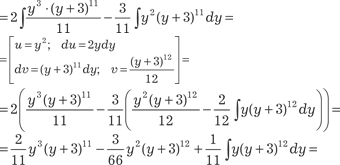

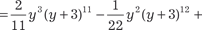
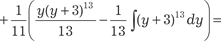
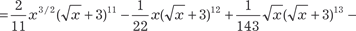
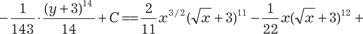
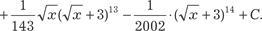
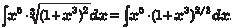
 . Поэтому имеем случай 2 и применяем подстановку (1 + х 3) = y 3 → х 3 = y 3 − 1;
. Поэтому имеем случай 2 и применяем подстановку (1 + х 3) = y 3 → х 3 = y 3 − 1;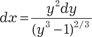 .
.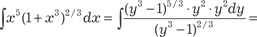
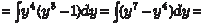
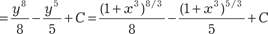
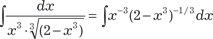
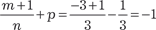
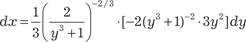
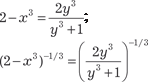 ;
;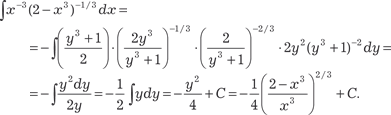
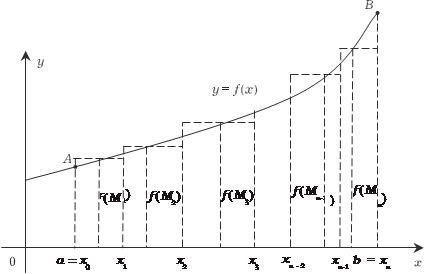 Найдем площадь криволинейной трапеции, т. е. фигуры, которая ограничена осью 0 х, графиком непрерывной функции y = f (x) и двумя прямыми x = a и x = b (рис. 5.2). Пока будем считать, что криволинейная трапеция расположена над осью 0х, т. е. f (x) > 0.
Найдем площадь криволинейной трапеции, т. е. фигуры, которая ограничена осью 0 х, графиком непрерывной функции y = f (x) и двумя прямыми x = a и x = b (рис. 5.2). Пока будем считать, что криволинейная трапеция расположена над осью 0х, т. е. f (x) > 0.
 (5.7)
(5.7)
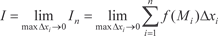
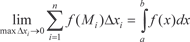 . (5.10)
. (5.10) ,
,