Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кільця головних ідеалів та евклідові кільця.
Означення. Область цілісності Приклад. Кільце Внаслідок того, що
Згідно з другою умовою з означення ідеалу
тобто ідеал Означення. Область цілісності
причому Приклад. Кільце Справді, за теоремою про ділення з остачею
якщо
Останні співвідношення можна переписати так:
Із формул (1) і (2) виходить:
Це означає, що коли кожному ненульовому цілому числу Теорема 2. Всяке евклідове кільце Доведення. Треба довести, що всякий ідеал
Очевидно, що За означенням евклідового кільця
На підставі другої умови з означення ідеалу
На області цілісності з одиницею вдається розповсюдити багато відомих ефектів теорії подільності в кільці цілих чисел. Нехай
Елемент Зауважимо, що сукупність усіх дільників 1 утворює мультиплікативну групу. Цю групу дільників називають мультиплікативною групою кільця К. Справді, якщо ( Виконання аксіом групи очевидне. Відзначимо, що всякий дільник а = а Елементи а, b
З цих рівностей виходить, що а = а(dc) і. Значить dc =1, тобто d і c –дільники 1. Таким чином, асоційовні елементи відрізняються тільки дільниками 1. Елементи а ≠ 0 і з кільця К називається незвідним, якщо він не є дільником 1, і якщо із рівності а = bc (b, c Елемент d 1. a 2. Теорема 1. Для всяких одночасно не рівних нулю елементів а, b із кільця К головних ідеалів існує їх найбільший спільний дільник d
Доведення. Розглянемо ідеал І = { ax + by | x, y Відзначимо, що найбільший спільний дільник елементів a, b Î K визначається неоднозначно: якщо d =(a, b), то e d =(a, b), де e – довільний дільник одиниці. Теорема 2. Якщо р – незвідний елемент кільця головних ідеалів К і елементів a, b Î K є таким, що р/ab, то р/а або р/b.
Доведення. Нехай р не є дільником а, і нехай d =(a, р). Покажемо, що d – дільник 1. Справді, якщо d не був дільником 1, то внаслідок незвідності елемента р подільності р де e - деякий дільник 1.Тоді d =р e -1 і, в силу подільності а Оскільки e =(a, р), то за теоремою 1 ($ x 0, y 0 Î K): e = ax 0 +р y 0 Помножимо цю рівність на b, матимемо e q =(ab) x 0 +р(y 0 b). Оскільки за умовою ab і р, то обидва доданки правої частини діляться на р і, значить, e b і р, тобто $ q Î K: e b = pq або інакше b = р(e -1 q), що означає b Таким чином, якщо ab Елементи р1,р2,…,рn такі, що а= e р1р2…рn /2/ причому в двох таких розкладах а= e р1р2…рn а= e ’ q 1 q 2 … q 3 r = 1 та існуютьтакі дільники одиниці e 1 e 2 … e r,що можливо після перестановки індексів, рі= e і qі (і=1,2,…, r). Лема 1. В кльці К головних ідеалів не існує нескінченного строго зростаючого ланцюжка ідеалів. (а 1)Ì(а2) Ì … Ì (аn)Ì… /3/ Доведення. Нехай ми маємо деяку строго зростаючий ланцюжок ідеалів (3) і І= Пересвідчимося в тому, що множина І є ідеалом. Виконання першої умови з означення ідеалу випливає з того, що коли a, b Î I, тобто a, b Î Нехай для означеності n То аk Î (аn) тобто, виконується і друга умова з означення ідеалу. Оскільки в кільці К кожен ідеал головний, то ($ c Î I) I =(с).Породжуючий елемент с ідеалу І належить І = Лема 2. Головні ідеали (a) i (b) кільця К тоді і тільки тоді співпадають коли (a) i (b)асоційовані. Доведення. Якщо (a) =(b), то а Î (b), b Î (a), внаслідок чого $ k1, k2 Î Z: а=bk1, b= аk2, що і означає асоційованість елементів a i b. Навпаки, нехай елементи a i b асоційовані, тобто а= b e, де e - дільник І. Тоді (" а1 Î (а))($ k 1 Î К): а= а k1 Значить, а1 = b (e k 1), внаслідок чого а1 Î (b). Звідси виходить, що (a) Ì (b). Аналогічно (b) Ì (а). Таким чином, (a) =(b). Будемо допускати, що в роскладі (2) індекс r приймати і значення 0. Тим самим домовимося вважати, що всякий дільник І на розкладі не незвідний елемент. Теорема 3. (Основна теорема теорії кілець головних ідеалів). Всякий не нульовий елемент кільця К головних ідеалів допускає одночасний розклад на незвідні елементи. Доведення. І. Доведемо спочатку, що для кожного елемента із кільця К існує розклад на незвідні елементи, тобто, що кожен елемент із К можна подати у вигляді (2) Нехай а≠0 – довільний елемент із К. Оскільки деякий дільник І є дільником і елемента а, то а завжди можна подати у вигляді a = bc (bc Î K) (4) Якщо із цього подання виходить, що b або с дільники І, то а є або дільником І або незвідним елементом і подання (4) треба розглядати як розклад елемента а на незвідні елементи.
Якщо у формулі (4) b і с – не дільники І, то до них можна застосувати ті ж міркування, які були застосовані до а. В результаті одержимо b = b 1 b 2, с=с1с2 (b 1, b 2, с1, с2 Î К) і, значить, а= b 1 b 2 с1с2 Можливі два випадки: 1) кожен з множників b 1, b 2, с1, с2 є або, дільником І або незвідним елементом. 2) серед елементів b 1, b 2, с1, с2 принаймі один не є ні дільником І, ні незвідним елементом. В першому випадку для елемента а справедливий розклад (2), в другому – наші міркування треба застосувати до тих із елементів b 1, b 2, с1, с2 які не є ні дільниками І ні незвідними елементами. Міркуючи таким способом дальше, після певного числа кроків дістанемо а= e а1а2…аn, (5) де e - дільник І і а1,а2,…,аn, - не дільники І запровадимо позначення а1’=а2…аn, а2’=а2…аn, аn1’=аn. Тоді а=(e а1)а1’а1’=а2а2’аn’=аn-1аn-1 Внаслідок чого справедливе включення (а)Ì(а1 ’)Ì (а2 ’)Ì…Ì (аn-1’), /6/ Які згідно з лемою 2 є строгими, бо породжуючі елементи цих ідеалів неасоційовані. Якщо в представленні (5) всі елементиа1, а2,…..аn– незвідні, то це означає. Що для а справедливий розклад /2/. Якщо ж декотрі із цих елементів не є незвідними, то процес міркування треба продовжити. Одначе, цей процес може бути нескінченним, тому що тоді строго зростаючий ланцюг /6/ головних ідеалів був би теж нескінченним, що на підставі леми неможливо. Отже, процес наших міркувань скінченний і після скінченного числа кроків одержимо для елемента а розклад /2/. ІІ. Доведемо тепер, що розклад кожного елемента а Припустимо, що деякий елемент а А= ξр1 р2… р r , а= ξ ’ q 1 q 2 … qj На незвідні множники. Тоді ξр1 р2… рr= ξ’q1q2…qj Або інакше (ξ’)-1 ξр1 р2… р r = q 1 q 2 … qj /7/ Ліва частина цієї рівності ділиться на р1, тому і права q 1 q 2 … qr ділиться на р 1. Оскільки р1 незвідний елемент, то за теоремою 2, яку по індукції можна поширити на довільне скінченне число співмножників, котрийсь із елементів q 1 q 2 … qj ділиться на р 1. Пронумерувати в разі потреби елементи q 1 q 2 … qj, доб’ємося того, що q 1 і р1. Оскільки q 1 і р1 – незвідні елементи, то існує дільник одиниці ξ 1 такий що, q 1 = ξ1 р1 Підставивши одержаний вираз замість q1 у формулу /7/ і скоротивши на р1 (на недільники нуля скорочувати можна), матимемо ξ1-1 (ξ’)-1 ξр1 р2… р r = q 1 q 2 … qj ліва частина цієї рівності ділиться на р2. Тоді на р2 ділиться і права. Провівши ті ж міркування, які були застосовані вище, матимемо
q 2 = ξ2р2, ξ2-1ξ1-1 (ξ’)-1 ξр3… р r = q 3 … qj якби будо r>1 то після r кроків мали б ξ2-1… ξ1-1 (ξ’)-1ξ= qr +1 … qj або інакше І = ξ-’ ξ’ ξ1… ξr qr +1 … qj ця рівність означає, що незвідні елементи qr +1 … qj є дільники І, а це суперечить їх незвідності. Отже r>І. лема логічно показує, що нерівність І>r теж неможлива. Таким чином І=r і справедливі одержані в процесі доведення рівності q 1 = ξ1 р1, q 2 = ξ2 р2,… qr = ξ r р r. Теорема доведена. На закінчення даної теми відзначимо, що в області цілісності з І, яка не є кільцем головних ідеалів, розклад на незвідні елементи може бути неоднозначним. Наведемо приклад. Легко перевірити, що сукупність z ( З цією метою у відповідність кожному числу z= а+ b (" z, z1, z2 є z( (Показати самостійно!). Зокрема, якщо 1= z1 × z2 (z1, z2 є z( Можливість розкладу числа z є z( N (z) і якщо z ¹ 0, то N (z) > 0. При N (z)=1, як показано вище, z ± 1, а за домовленістю дільники 1 мають розклади на незвідні. Припустимо, що твердження вірне для всіх чисел з нормою меншою від m, тобто припустимо, що всі числа При z, для яких N (z) < m, мають розклади на незвідні числа із z( z= z1 × z2(z1, z2 є z( Якщо із цього подання випливає, що z1 або z2 – дільники 1, то за означенням z – незвідний елемент і він має тривіальний розклад на незвідні множники: z= e z (e =1). Якщо ні z1 ні z2 – не дільники 1, тобто z1, z2= ± 1, то N (z1), N (z2) ¹ 1 із представлення N (z) = N (z1) × N (z2) випливає, що N (z1) < m і N (z2) < m. Тоді за індуктивним припущенням z1 і z2 можна розкласти на незвідні множники. Підставивши ці розклади у формулу /8/, одержимо розклад і для елемента z. Таким чином, кожен елемент із кільця z( 4=2×2, 4=(1+ В цих розкладах числа 2, 1± §5. Конгруенції та фактор кільця за ідеалом. 1. Конгруенції комутативного кільця К за ідеалам І.
Крім алгебраїчних операцій в кільці К можуть бути введені і деякі інші відношення, зокрема, відношення еквівалентності. З алгебраїчної точки зору інтерес представляють тільки такі відношення еквівалентності, які певним способом узгодженні з операціями, означеними в кільці. Означення. Говорять, що відношення еквівалентності a ~ b в комутативному кільці К узгоджено з алгебраїчними операціями цього кільця, якщо: (" a, b, c, d є К):(a~b)Ù(c ~d)Þ(a + c ~ b + d)Ù(ac ~ bd) Прикладом відношення еквівалентності, узгодженого з операціями кільця, служить відношення конгруентності за модулем ідеалу. Означення. Говорять, що елементи a, b комутативного кільця конгруентні між собою, за ідеалом І Ì К і за модулем ідеалу І, якщо a - b a º b (modI) Теорема 1. Відношення конгруентності за ідеалом І кільця К відношенням еквівалентності в К, узгодженим з операціями К. Доведення. Оскільки кожен ідеал І кільця К є підкільцем, отже, і підгрупою групи цього кільця, то перевірка того, що відношення конгруентності за ідеалом І є відношення еквівалентності. Узгодженим з операцією додавання, приводиться точно так, як і в теорії груп. І тому зараз проводити її не будемо. Покажемо тільки, що коли a º b (mod I), c º d (mod I), /1/ то ac º bd (mod I) /2/ з цією метою розглянемо різницю ac – bd ac-bd=(ac – bd) + (bc – bd) = (a-b)c +b(c-d) /3/ в силу конгруенції /1/ a-b, c-d Виявляється, що відношення конгруентності за ідеалом І вичерпуються усі відношення еквівалентності, узгодженні з операціями кільця. Точніше справедлива теорема 2. Теорема 2. Для всякого відношення еквівалентності в кільця К, узгодженого з операціями цього кільця, існує ідеал І такий, що дане відношення еквівалентності є відношення конгруентності за ідеалом І. Доведення цієї теореми проводити не будемо. 2.Фактор-кільця комутативного кільця за ідеалом І. Добре відомо, що всяке відношення еквівалентності на множені І породжує розбитя цієї множини на класи, класи еквівалентності. Та відношення конгруентності за модулем ідеалу І в кільці К породжує розбиття кільця К на класи. Ці класи називають суміжними класами або класами елементів. Конгруентних за ідеалом І. Означення Суміжним класом комутативного кільця К за ідеалом або класу елементів, конгруентних за ідеалом І кільця К називають всякий клас еквівалентності відношенням конгруентності за ідеалом І, тобто. Сукупність С а усіх елементів кільця К, які конгруентні елементу а Як уже відзначалося, кожен ідеал І кільця К є підгрупою адитивної групи кільця К і, значить, відношення конгруентної в кільці К за ідеалом І є відношенням конгруентності в адитивній групі кільця К за підгрупою І, а кожен суміжний клас кільця К за ідеалом І є суміжним класом адитивної групи кільця К за підгрупою І. Тому суміжні класи кільця К за ідеалом І мають таку ж структуру, як і суміжні класи адитивної абелевої групи за підгрупою, тобто, справедлива така теорема. Теорема 3. Всякий суміжний клас Са комутативного кільця К за ідеалом І можна подати у вигляді Са = а + І, де а — довільний елемент класу Са. Навпаки, всяка множина а + І, де а — довільний елемент кільця К, утворює суміжний клас кільця К за ідеалом І. Нагадаємо, що за означенням
Розглянемо сукупність К / І усіх суміжних класів комутативного кільця К за ідеалом І
Як відомо, у випадку адитивної абелевої групи ця сукупність утворює групу, так звану фактор-групу. У випадку кільця сукупність К/І є кільцем. Теорема 4. Сукупність К / І усіх суміжних класів комутативного кільця К за ідеалом І є комутативним кільцем. Якщо кільце К містить І, то і кільце К / І містить одиницю. Кільце К / І називають фактор-кільцем кільця К за ідеалом І. Доведення. Сукупність К / І можна розглядати як сукупність суміжних класів адитивної групи кільця К за підгрупою І, а така сукупність, як відомо з теорії груп, утворює адитивну абелеву групу, фактор-групу групи К за підгрупою І, причому операція додавання задається формулою:
Тому для завершення доведення теореми треба тільки ввести у множині К / І операцію множення і перевірити, що вона є асоціативною, комутативною і пов’язана з додаванням дистрибутивним законом. Операцію множення суміжних класів задамо так:
Покажемо, що так означене множення є однозначне, тобто, що за формулою у відповідність суміжним класам а+І та b +І ставиться єдиний суміжний клас ab + І. Неоднозначність може виникнути за рахунок того, що в поданні суміжного класу у виді а+І елемент а є довільним елементом цього класу. Значить, якщо
Тоді Доведемо, що це насправді так. Належності
Тоді а b +І = а1 b 1 +І Цим однозначність множення доведена. Асоціативність множення класів випливає із асоціативності множення в К:
Аналогічно доводиться комутативність множення класів. Так само аналогічно виводиться дистрибутивність:
Якщо в кільці К є одиниця, то, очевидно клас 1+І — одиниця фактор-кільця К / І.
|
|||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.240.61 (0.109 с.) |
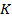 з
з 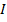 , кожен ідеал якої є головним називається кільцем головних ідеалів.
, кожен ідеал якої є головним називається кільцем головних ідеалів. цілих чисел є кільцем головних ідеалів. Дійсно, нехай
цілих чисел є кільцем головних ідеалів. Дійсно, нехай  то
то  . Тому вважатимемо, що
. Тому вважатимемо, що  . Тоді
. Тоді  .
.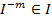 . Це означає, в кожному ідеалі є натуральне число. Нехай
. Це означає, в кожному ідеалі є натуральне число. Нехай  – найменше з усіх натуральних чисел ідеалу
– найменше з усіх натуральних чисел ідеалу 
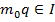 , а згідно з першою
, а згідно з першою  . Це означає, що коли було б
. Це означає, що коли було б 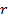 , менше за
, менше за  і, отже,
і, отже, 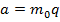 . Таким чином,
. Таким чином, :
:  .
.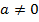 поставлено у відповідність натуральне число
поставлено у відповідність натуральне число  так, що
так, що

 цілих чисел є евклідовим кільцем.
цілих чисел є евклідовим кільцем. (1)
(1)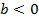 то
то  і значить,
і значить, ,
,  .
. (2)
(2)
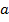 поставити у відповідність його абсолютну величину, тобто покласти
поставити у відповідність його абсолютну величину, тобто покласти  , то
, то  , то кожному його ненулевому елементові а поставлено у відповідність натуральне число
, то кожному його ненулевому елементові а поставлено у відповідність натуральне число  множини натуральних чисел. В
множини натуральних чисел. В  є найменше число
є найменше число  . Інакше кажучи, в
. Інакше кажучи, в  такий, що
такий, що
 . Покажемо: що і навпаки
. Покажемо: що і навпаки  , звідси випливатиме потрібна рівність
, звідси випливатиме потрібна рівність 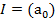 .
.
 , а на підставі першої – елемент
, а на підставі першої – елемент 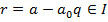 . Якби
. Якби  , то
, то  , що суперечить вибору елемента
, що суперечить вибору елемента  . Тому
. Тому 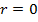 і, значить,
і, значить,  , тобто,
, тобто,  Подільність в областях цілісності з одиницею.
Подільність в областях цілісності з одиницею.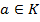 ділиться на елемент
ділиться на елемент 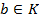 ,
, 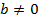 , якщо
, якщо
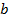 називають дільником
називають дільником  . Якщо
. Якщо  то елементи а, b
то елементи а, b 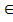 K називаються дільниками 1кільця K. З рівності
K називаються дільниками 1кільця K. З рівності  , та
, та  і, значить,
і, значить,  =(-1)
=(-1)  (-1)=1.
(-1)=1.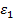 і
і  деякі дільники 1,то(
деякі дільники 1,то( ,
, 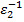 ):
):  =
= 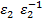 =1 Тоді
=1 Тоді )(
)( )=(
)=( одиниці є дільником довільного елемента а
одиниці є дільником довільного елемента а 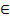 К, бо
К, бо 1=а(
1=а(  =
=  )
)
 , тобто, це прості числа і ті від’ємні, абсолютні величини яких прості.
, тобто, це прості числа і ті від’ємні, абсолютні величини яких прості.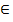 К, d =(a, d), якщо
К, d =(a, d), якщо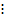 d, b
d, b  : (
: (
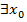 ,
,  К: d =а
К: d =а  + b
+ b 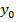
 d ми мали б: р= e d,
d ми мали б: р= e d, р. Отже, d – дільник 1. d = e.
р. Отже, d – дільник 1. d = e. р.
р. -обєднання всіх ідеалів цього ланцюжка.
-обєднання всіх ідеалів цього ланцюжка.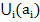 , то ($ n, m):(а Î (аn)) Ç (b Î (а m)),
, то ($ n, m):(а Î (аn)) Ç (b Î (а m)),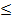 m. Тоді (аn)<(am) і, значить, a, b Î (а m). Оскільки (am) – ідеал, то а–b Î (а m), внаслідок чого а-b Î
m. Тоді (аn)<(am) і, значить, a, b Î (а m). Оскільки (am) – ідеал, то а–b Î (а m), внаслідок чого а-b Î  , c Î (а1). Тоді І =(с) Ì (а1), але і І – об’єднання всіх ідеалів (а і), тому (а1) Ì І. Із включень І Ì (а1) і (а1) Ì І виходить, що І=(а1), це і означає, що (а1) – останній ідеал ланцюжка (3), чим лема доведена.
, c Î (а1). Тоді І =(с) Ì (а1), але і І – об’єднання всіх ідеалів (а і), тому (а1) Ì І. Із включень І Ì (а1) і (а1) Ì І виходить, що І=(а1), це і означає, що (а1) – останній ідеал ланцюжка (3), чим лема доведена. ) комплексних чисел виду а+ b
) комплексних чисел виду а+ b  і)(1-
і)(1-  К, і значить конгруентні між собою за ідеалом І.
К, і значить конгруентні між собою за ідеалом І.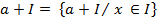
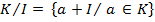

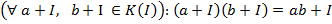
 , то
, то  .
. і щоб множення було однозначним, має бути справедлива рівність
і щоб множення було однозначним, має бути справедлива рівність 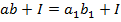 .
.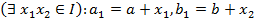
 звідки виходить, що класи ав+І і а1в1+І мають спільний елемент а1в1,і тому вони співпадають:
звідки виходить, що класи ав+І і а1в1+І мають спільний елемент а1в1,і тому вони співпадають: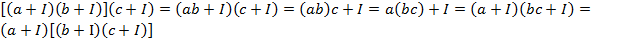 .
.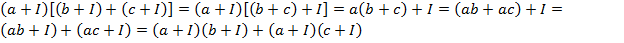 .
.