Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление определителя разложением по строке или столбцу
Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения:
Пример. Вычислить определитель путем разложения по 1-ой строке и второму столбцу. Решение. По первой строке: По второму столбцу: Определение 15. Матрица называется невырожденной, если ее определитель не равен нулю и вырожденной в противном случае. Замечание (об обратной матрице). В алгебре матриц нет понятия деления матриц. Для невырожденных матриц существует обратная матрица. Определение 16. Матрица Теорема о вычислении обратной матрицы. Если А невырожденная (
Пример. Найти матрицу, обратную данной, проверить правильность вычисления.
1) 2) Найдем алгебраические дополнения:
3) Составим обратную матрицу
Проверим вычисления по формуле
Понятие о ранге матрицы. Пусть дана матрица А размером
Выберем произвольно в этой матрице k строк и k столбцов. Элементы, стоящие на пересечении этих строк и столбцов, образуют квадратную матрицу k -го порядка
Определение 17. Наивысший порядок отличных от нуля миноров называется рангом матрицы. Обозначается ранг матрицы Пример. Найти ранг матрицы
При вычислении ранга матрицы переходят от вычисления миноров меньших порядков к минорам больших порядков. Если Второй способ основывается на элементарных преобразованиях матрицы. Элементарными преобразованиями называются следующие: 1. перестановка строк (столбцов), 2. умножение строки (столбца) на число, не равное нулю, 3. прибавление к строке (столбцу) другой строки (столбца), умноженной на число,
4. вычеркивание нулевых строк (столбцов), 5. вычеркивание строки (столбца), являющегося линейной комбинацией других строк (столбцов). Элементарные преобразования не изменяют ранга матрицы. Если удастся путем элементарных преобразований привести матрицу к трапециевидной форме, то ее ранг будет равен числу ее ненулевых строк.
При приведении матрицы к трапециевидной форме удобно пользоваться численным методом Гаусса: 1) переставляя строки, добиваемся, чтобы 2) умножаем первую строку на числа ( 3) не трогая первой строки, добиваемся, чтобы 4) умножаем вторую строку на числа ( 5) и т.д. Пример. Найти ранг матрицы
в матрице две ненулевые строки, следовательно, Системы линейных уравнений. П. 1. Основные понятия.
Определение 18. Система уравнений вида
называется системой m линейных уравнений с n неизвестными Если все bi = 0 (i = 1, 2, 3,…, m), то система называется однородной, в противном случае неоднородной. Матрица, состоящая из коэффициентов при неизвестных, называется матрицей системы. Матрица, состоящая из коэффициентов при неизвестных и столбца свободных членов, называется расширенной матрицей системы.
Матричная запись системы линейных уравнений имеет вид:
Определение 19. Система уравнений, имеющая хотя бы одно решение, называется совместной и несовместной, если она не имеет ни одного решения.
Определение 20. Система называется определенной, если имеет одно решение, и неопределенной, если решений более одного. Определение 21. Решением системы (*) называется всякая совокупность чисел Элементарные преобразования системы (только над строками): 1. перестановка уравнений, 2. умножение уравнения на число, отличное от нуля, 3. прибавление к уравнению другого уравнения, умноженного на число. Выполняют элементарные преобразования над расширенной матрицей системы и лишь над строками, так как перестановка столбцов соответствует переобозначению неизвестных.
|
||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.65.233 (0.019 с.) |
 - разложение определителя по i -той строке.
- разложение определителя по i -той строке. - разложение определителя по j- тому столбцу.
- разложение определителя по j- тому столбцу. .
. .
. называется обратной к матрице А, если
называется обратной к матрице А, если  , где Е – единичная матрица.
, где Е – единичная матрица. ) матрица порядка n, то обратная к ней матрица находится по формуле
) матрица порядка n, то обратная к ней матрица находится по формуле  , где
, где  – присоединенная (союзная) матрица, то есть транспонированная матрица, составленная из алгебраических дополнений.
– присоединенная (союзная) матрица, то есть транспонированная матрица, составленная из алгебраических дополнений.
 .
. , следовательно, матрица А – невырожденная.
, следовательно, матрица А – невырожденная.








 :
:
 :
:


 :
:




 .
. . Определитель матрицы будем называть минором k -го порядка матрицы А.
. Определитель матрицы будем называть минором k -го порядка матрицы А. или
или  .
. ;
; ;
;  ;
; 
 .
. , то всякий отличный от нуля минор порядка
, то всякий отличный от нуля минор порядка  называется базисным минором. Этот метод вычисления ранга матрицы называется методом окаймляющих миноров.
называется базисным минором. Этот метод вычисления ранга матрицы называется методом окаймляющих миноров. и
и  , последнее можно достичь (если в первом столбце нет единиц) путем деления всей строки на
, последнее можно достичь (если в первом столбце нет единиц) путем деления всей строки на  . Первую строку называют рабочей, а элемент
. Первую строку называют рабочей, а элемент  – ведущим.
– ведущим. ), где
), где  , прибавляем ее соответственно ко второй и т.д. m-ой строке, получаем в 1-ом столбце под
, прибавляем ее соответственно ко второй и т.д. m-ой строке, получаем в 1-ом столбце под  и
и  путем деления всей строки на
путем деления всей строки на  или путем перестановки строк. Теперь вторая строка стала рабочей, а элемент
или путем перестановки строк. Теперь вторая строка стала рабочей, а элемент  – ведущим.
– ведущим. ), где
), где  , прибавляем ее соответственно к третей и т.д. m-ой строке, получаем во 2-ом столбце под
, прибавляем ее соответственно к третей и т.д. m-ой строке, получаем во 2-ом столбце под  . Решение.
. Решение. ~ (меняем строки местами)
~ (меняем строки местами) 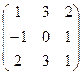 ~ (первую строку прибавляем ко второй)
~ (первую строку прибавляем ко второй)  ~ (первую строку умножаем на (-2) и прибавляем к третьей)
~ (первую строку умножаем на (-2) и прибавляем к третьей)  ~ (прибавляем ко второй строке третью)
~ (прибавляем ко второй строке третью)  ~
~  ,
, .
. (*)
(*) ,
,  , …,
, …,  .
. – матрица системы,
– матрица системы,  – расширенная матрица системы,
– расширенная матрица системы, – столбец свободных членов,
– столбец свободных членов,  – столбец неизвестных.
– столбец неизвестных. .
. ,
,  , …,
, …,  , которая, будучи подставлена в систему (8) вместо неизвестных
, которая, будучи подставлена в систему (8) вместо неизвестных 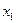 ,
,  , …,
, …, 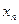 , обращает все уравнения системы в тождества.
, обращает все уравнения системы в тождества.