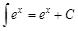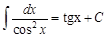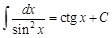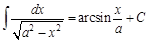Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первообразная функции и неопределенный интегралСодержание книги
Поиск на нашем сайте В §1 мы рассматривали задачи, приведшие к появлению дифференциального исчисления, и говорили о том, что зная выражение некоторой функции, можно найти скорость ее изменения. Часто в математике и ее приложениях требуется решить обратную задачу: по известной производной найти функцию, от которой она была взята. Такую задачу, например, представляет нахождение закона изменения координаты тела с течением времени по известному закону изменения скорости этого тела. Зная, что скорость есть производная пути по времени, нужно определить функцию для пути. Функцию, восстанавливаемую по ее известной производной и дифференциалу, называют первообразной. Функцию
Так для функции Получается, что функции И вообще, если функция
Неопределенным интегралом от функции Отметим основные свойства неопределенного интеграла. Свойство 1. Если функция Свойство 2. Если Свойство 3. Постоянный множитель можно выносить за знак интеграла Свойство 4. Если функции Формулы для неопределенных интегралов от некоторых элементарных функций могут быть получены исходя из того, что интегрирование представляет собой математическую операцию, обратную дифференцированию. Интегралы, приведенные в этой таблице, часто называют основными табличными интегралами.
Рассмотрим некоторые способы вычисления неопределенных интегралов.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |
|||||||||||||||||||||||||||||||||||||||||||||

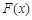 называют первообразной для функции
называют первообразной для функции  на некотором промежутке, если для всех значений
на некотором промежутке, если для всех значений 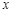 из этого промежутка выполняется равенство:
из этого промежутка выполняется равенство: .
. первообразной на множестве
первообразной на множестве  будет функция
будет функция 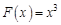 , так как
, так как  для каждого
для каждого  . Но и функция
. Но и функция  также будет являться первообразной для функции
также будет являться первообразной для функции  , так как
, так как  . И функции
. И функции  ,
,  будут первообразными для функции
будут первообразными для функции  . Да и вообще, любая функция
. Да и вообще, любая функция 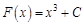 , где
, где  константа, будет являться первообразной для указанной функции
константа, будет являться первообразной для указанной функции  , так как ее производная будет равна
, так как ее производная будет равна  .
. является первообразной для функции
является первообразной для функции 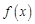 на некотором промежутке, то множество всех первообразных для функции
на некотором промежутке, то множество всех первообразных для функции  на этом промежутке задается формулой
на этом промежутке задается формулой  , где
, где  . Это действительно так, ведь:
. Это действительно так, ведь: .
. называют семейством первообразных, а константу
называют семейством первообразных, а константу  – произвольной постоянной.
– произвольной постоянной. . Читают «интеграл эф от икс дэ икс». Символ
. Читают «интеграл эф от икс дэ икс». Символ  называют знаком интеграла, функцию
называют знаком интеграла, функцию  – подынтегральным выражением, x – переменной интегрирования.
– подынтегральным выражением, x – переменной интегрирования. , а
, а  .
. и
и  .
. .
.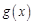 имеют первообразные, то
имеют первообразные, то  , то есть интеграл суммы двух функций равен сумме интегралов этих функций.
, то есть интеграл суммы двух функций равен сумме интегралов этих функций.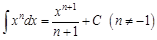

 ,
,