Описание сложных, изменяющихся со временем процессов, протекающих в реальной жизни, с помощью элементарной математики практически невозможно, так как используемые для этого величины сами изменяются. Высшая математика оперирует величинами и зависимостями, подверженными изменениям, происходящим по различным законам.
 В высшей математике величиной, определяющей быстроту изменения функциональной зависимости, является производная функции. Введем это понятие. Для этого обратимся к рис. 2, на котором графически представлена некоторая произвольная функциональная зависимость
В высшей математике величиной, определяющей быстроту изменения функциональной зависимости, является производная функции. Введем это понятие. Для этого обратимся к рис. 2, на котором графически представлена некоторая произвольная функциональная зависимость 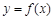 . Отметим на графике значения аргумента
. Отметим на графике значения аргумента 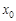 и
и  , разница между которыми есть приращение аргумента:
, разница между которыми есть приращение аргумента: 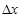 . Тогда
. Тогда 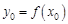 и
и  – соответственно значения функции в этих точках, где
– соответственно значения функции в этих точках, где  называют приращением функции.
называют приращением функции.
Рассмотрим отношение  . Оно характеризует целый интервал. Чтобы достигнуть поставленной цели: знать значение величины в каждой точке в каждый момент времени, устремим
. Оно характеризует целый интервал. Чтобы достигнуть поставленной цели: знать значение величины в каждой точке в каждый момент времени, устремим  к нулю (
к нулю ( ), то есть стянем этот интервал практически к точке, к предельно малому значению. Тогда и
), то есть стянем этот интервал практически к точке, к предельно малому значению. Тогда и  будет стремиться к нулю (
будет стремиться к нулю ( ). Получим предел отношения
). Получим предел отношения  . Если этот предел существует, то его называют производной функции
. Если этот предел существует, то его называют производной функции 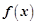 в точке
в точке  и обозначают
и обозначают 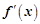 . Таким образом:
. Таким образом:
 или
или  .
.
Итак, производной функции 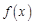 в точке
в точке 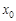 называют предел отношения приращения функции
называют предел отношения приращения функции  в точке
в точке 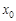 к приращению аргумента
к приращению аргумента 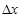 при стремлении последнего к нулю.
при стремлении последнего к нулю.
Операцию нахождения производной функции называют дифференцированием этой функции. Функцию, имеющую производную в некоторой точке 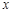 , называют дифференцируемой в этой точке.
, называют дифференцируемой в этой точке.
Выявим геометрическое толкование производной. Используем рис. 2. На нем графически изображена некоторая функция  . При значении аргумента
. При значении аргумента 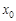 функция имеет значение
функция имеет значение 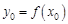 . На линии графика эти координаты определяют точку
. На линии графика эти координаты определяют точку  . Если аргументу функции дать приращение
. Если аргументу функции дать приращение  , то новому значению аргумента
, то новому значению аргумента  будет соответствовать значение функции
будет соответствовать значение функции 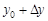 . Эти значения определят точку
. Эти значения определят точку  . Проведем секущую
. Проведем секущую 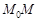 и обозначим через
и обозначим через  угол между этой секущей и положительным направлением оси
угол между этой секущей и положительным направлением оси  . Тогда тангенс этого угла равен:
. Тогда тангенс этого угла равен:
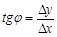 .
.
Если теперь мы будем стягивать интервал  , то точка
, то точка 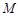 , перемещаясь вдоль кривой, будет стремиться к точке
, перемещаясь вдоль кривой, будет стремиться к точке  Секущая будет поворачиваться около точки
Секущая будет поворачиваться около точки  , и угол
, и угол  будет изменяться. При
будет изменяться. При 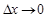 угол
угол  будет стремиться к некоторому конечному пределу
будет стремиться к некоторому конечному пределу  , а секущая
, а секущая 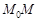 к касательной к графику, проходящей через точку
к касательной к графику, проходящей через точку  . Тогда:
. Тогда:
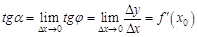 .
.
Таким образом получаем, что значение производной функции 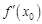 при заданном значение аргумента
при заданном значение аргумента  равно угловому коэффициенту касательной, проведенной к графику функции в данной точке
равно угловому коэффициенту касательной, проведенной к графику функции в данной точке  . В этом заключается геометрический смысл производной.
. В этом заключается геометрический смысл производной.
С понятием производной функции тесно связано понятие ее дифференциала. Введем это понятие.
Пусть есть функция, определенная в каждой точке на некотором отрезке [ a, b ], и дифференцируемая в каждой точке  , принадлежащей отрезку [ a, b ]. Производная этой функции определяется так:
, принадлежащей отрезку [ a, b ]. Производная этой функции определяется так:
 .
.
Опираясь на определение предела функции, можно записать:
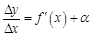 ,
,
где  – малая величина, которая стремиться к нулю
– малая величина, которая стремиться к нулю  при
при 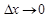 . Умножим последнее равенство на
. Умножим последнее равенство на 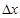 . Получим:
. Получим:
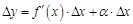 .
.
Слагаемое 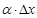 из-за малости обоих сомножителей является бесконечно малой величиной более высокого порядка, чем
из-за малости обоих сомножителей является бесконечно малой величиной более высокого порядка, чем 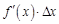 , и его можно не учитывать в уравнении. Тогда слагаемое
, и его можно не учитывать в уравнении. Тогда слагаемое  является основной частью уравнения, линейной относительно
является основной частью уравнения, линейной относительно 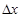 .
.
Произведение 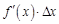 называют дифференциалом функции, обозначают
называют дифференциалом функции, обозначают  или
или 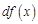 и записывают:
и записывают:
 .
.
Найдем дифференциал независимой переменной  :
:
 ,
,  , следовательно
, следовательно  , тогда
, тогда 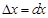 .Заменив в формуле дифференциала функции
.Заменив в формуле дифференциала функции 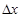 на
на 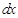 , получим:
, получим:
 .
.
Откуда:
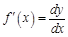 .
.
Таким образом, можно сказать, что производная функции есть отношение дифференциала функции к дифференциалу аргумента.
Обозначение 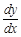 читают так «дэ игрек по дэ икс». Символы дифференциалов
читают так «дэ игрек по дэ икс». Символы дифференциалов  нельзя сокращать.
нельзя сокращать.
Выясним геометрический смысл дифференциала.
 Рассмотрим дифференцируемую функцию
Рассмотрим дифференцируемую функцию  на интервале [ a, b ]. Ее график изображен на рис. 3. Из рисунка видно, что
на интервале [ a, b ]. Ее график изображен на рис. 3. Из рисунка видно, что 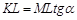 .
.  , а
, а  . Тогда
. Тогда  .
.  . Тогда можно сказать, что геометрическое истолкование дифференциала следующее: если функция
. Тогда можно сказать, что геометрическое истолкование дифференциала следующее: если функция 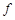 имеет производную в точке
имеет производную в точке 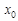 , то дифференциал функции
, то дифференциал функции 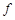 в этой точке равен приращению ординаты касательной, проведенной к графику функции в точке с абсциссой
в этой точке равен приращению ординаты касательной, проведенной к графику функции в точке с абсциссой 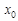 , при переходе от точки касания в точку с абсциссой
, при переходе от точки касания в точку с абсциссой  . Таким образом, дифференциал – это линейная часть приращения функции, то есть часть приращения отсекаемая касательной. Это видно на рис. 3:
. Таким образом, дифференциал – это линейная часть приращения функции, то есть часть приращения отсекаемая касательной. Это видно на рис. 3:  – это приращение функции, а
– это приращение функции, а  – ее дифференциал.
– ее дифференциал.
При малых приращениях аргумента функции 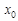 приращение функции приблизительно равно ее дифференциалу
приращение функции приблизительно равно ее дифференциалу 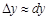 . Это приближение широко используют как в самой математике, так и в ее приложениях, поскольку оно позволяет легко и быстро вычислять приращение функции с незначительной погрешностью. Можно показать, что для дифференцируемой в точке
. Это приближение широко используют как в самой математике, так и в ее приложениях, поскольку оно позволяет легко и быстро вычислять приращение функции с незначительной погрешностью. Можно показать, что для дифференцируемой в точке  функции
функции 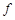 , у которой
, у которой  , при всех достаточно малых
, при всех достаточно малых 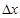 справедлива следующая формула:
справедлива следующая формула:
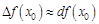 или
или  .
.
В общем случае производная функции  представляет собой скорость изменения этой функции при изменении ее аргумента. В этом состоит физический смысл производной функции. Это положение широко используется при решении ряда физических задач. В частности, как рассматривалось выше, мгновенная скорость прямолинейного движения материальной точки равна производной зависимости ее координаты от времени. И вообще, в случаях, когда рассматривают течение какого-либо процесса во времени, быстроту его протекания выражают через производную. Примеры этого мы встречаем при описании процесса изменения температуры тела при его нагревании или охлаждении, размножения бактерий (модели Мальтуса и Ферхюльста), изменении концентрации лекарственного препарата или индикатора в крови (фармакокинетическая модель) и пр. Вопрос об указанных моделях мы рассмотрим в §4 этого пособия.
представляет собой скорость изменения этой функции при изменении ее аргумента. В этом состоит физический смысл производной функции. Это положение широко используется при решении ряда физических задач. В частности, как рассматривалось выше, мгновенная скорость прямолинейного движения материальной точки равна производной зависимости ее координаты от времени. И вообще, в случаях, когда рассматривают течение какого-либо процесса во времени, быстроту его протекания выражают через производную. Примеры этого мы встречаем при описании процесса изменения температуры тела при его нагревании или охлаждении, размножения бактерий (модели Мальтуса и Ферхюльста), изменении концентрации лекарственного препарата или индикатора в крови (фармакокинетическая модель) и пр. Вопрос об указанных моделях мы рассмотрим в §4 этого пособия.


 В высшей математике величиной, определяющей быстроту изменения функциональной зависимости, является производная функции. Введем это понятие. Для этого обратимся к рис. 2, на котором графически представлена некоторая произвольная функциональная зависимость
В высшей математике величиной, определяющей быстроту изменения функциональной зависимости, является производная функции. Введем это понятие. Для этого обратимся к рис. 2, на котором графически представлена некоторая произвольная функциональная зависимость 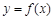 . Отметим на графике значения аргумента
. Отметим на графике значения аргумента 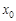 и
и  , разница между которыми есть приращение аргумента:
, разница между которыми есть приращение аргумента: 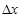 . Тогда
. Тогда 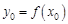 и
и  – соответственно значения функции в этих точках, где
– соответственно значения функции в этих точках, где  называют приращением функции.
называют приращением функции. . Оно характеризует целый интервал. Чтобы достигнуть поставленной цели: знать значение величины в каждой точке в каждый момент времени, устремим
. Оно характеризует целый интервал. Чтобы достигнуть поставленной цели: знать значение величины в каждой точке в каждый момент времени, устремим  к нулю (
к нулю ( ), то есть стянем этот интервал практически к точке, к предельно малому значению. Тогда и
), то есть стянем этот интервал практически к точке, к предельно малому значению. Тогда и  будет стремиться к нулю (
будет стремиться к нулю ( ). Получим предел отношения
). Получим предел отношения  . Если этот предел существует, то его называют производной функции
. Если этот предел существует, то его называют производной функции 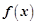 в точке
в точке  и обозначают
и обозначают 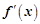 . Таким образом:
. Таким образом: или
или  .
.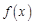 в точке
в точке  в точке
в точке 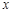 , называют дифференцируемой в этой точке.
, называют дифференцируемой в этой точке. . При значении аргумента
. При значении аргумента  . Если аргументу функции дать приращение
. Если аргументу функции дать приращение 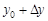 . Эти значения определят точку
. Эти значения определят точку  . Проведем секущую
. Проведем секущую 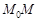 и обозначим через
и обозначим через  угол между этой секущей и положительным направлением оси
угол между этой секущей и положительным направлением оси  . Тогда тангенс этого угла равен:
. Тогда тангенс этого угла равен: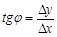 .
.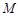 , перемещаясь вдоль кривой, будет стремиться к точке
, перемещаясь вдоль кривой, будет стремиться к точке  Секущая будет поворачиваться около точки
Секущая будет поворачиваться около точки  , и угол
, и угол 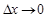 угол
угол  , а секущая
, а секущая 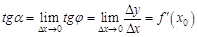 .
.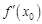 при заданном значение аргумента
при заданном значение аргумента  равно угловому коэффициенту касательной, проведенной к графику функции в данной точке
равно угловому коэффициенту касательной, проведенной к графику функции в данной точке  , принадлежащей отрезку [ a, b ]. Производная этой функции определяется так:
, принадлежащей отрезку [ a, b ]. Производная этой функции определяется так: .
.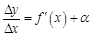 ,
, при
при 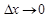 . Умножим последнее равенство на
. Умножим последнее равенство на 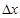 . Получим:
. Получим: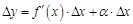 .
.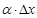 из-за малости обоих сомножителей является бесконечно малой величиной более высокого порядка, чем
из-за малости обоих сомножителей является бесконечно малой величиной более высокого порядка, чем 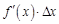 , и его можно не учитывать в уравнении. Тогда слагаемое
, и его можно не учитывать в уравнении. Тогда слагаемое  является основной частью уравнения, линейной относительно
является основной частью уравнения, линейной относительно 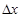 .
. или
или 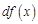 и записывают:
и записывают: .
. ,
,  , следовательно
, следовательно  , тогда
, тогда 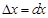 .Заменив в формуле дифференциала функции
.Заменив в формуле дифференциала функции 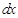 , получим:
, получим: .
.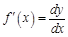 .
.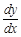 читают так «дэ игрек по дэ икс». Символы дифференциалов
читают так «дэ игрек по дэ икс». Символы дифференциалов  нельзя сокращать.
нельзя сокращать.  Рассмотрим дифференцируемую функцию
Рассмотрим дифференцируемую функцию  на интервале [ a, b ]. Ее график изображен на рис. 3. Из рисунка видно, что
на интервале [ a, b ]. Ее график изображен на рис. 3. Из рисунка видно, что 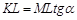 .
.  , а
, а  . Тогда
. Тогда  .
.  . Тогда можно сказать, что геометрическое истолкование дифференциала следующее: если функция
. Тогда можно сказать, что геометрическое истолкование дифференциала следующее: если функция 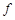 имеет производную в точке
имеет производную в точке 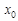 , то дифференциал функции
, то дифференциал функции  . Таким образом, дифференциал – это линейная часть приращения функции, то есть часть приращения отсекаемая касательной. Это видно на рис. 3:
. Таким образом, дифференциал – это линейная часть приращения функции, то есть часть приращения отсекаемая касательной. Это видно на рис. 3:  – ее дифференциал.
– ее дифференциал.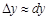 . Это приближение широко используют как в самой математике, так и в ее приложениях, поскольку оно позволяет легко и быстро вычислять приращение функции с незначительной погрешностью. Можно показать, что для дифференцируемой в точке
. Это приближение широко используют как в самой математике, так и в ее приложениях, поскольку оно позволяет легко и быстро вычислять приращение функции с незначительной погрешностью. Можно показать, что для дифференцируемой в точке  функции
функции  , при всех достаточно малых
, при всех достаточно малых 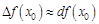 или
или  .
.