Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Возведение комплексного числа в степень и извлечение корня из комплексного числа. ⇐ ПредыдущаяСтр 8 из 8
Определение. Из формулы для произведения комплексных чисел следует формула Муавра: если
При возведении комплексного числа в натуральную степень модуль возводится в эту степень, а аргумент умножается на нее. Пример. Найти Решение.Возводим в шестую степень
= Определение. Корнем n-ой степени (n Пусть Меняя Пример. Вычислить
Перейдем из алгебраической формы в тригонометрическую:
При k=0 получим При k=1 получим При k=2 получим При k=3 получим
Полученные корни изобразим на комплексной плоскости:
Отметим, что точки плоскости являются вершинами правильного четырехугольника. Это не случайно – для любого
Входной контроль 1. Запишите формулу Муавра для возведения в степень 2. Запишите определение корня n-ой степени Ход работы 1.Найти: 2.Вычислить корни и изобразить на комплексной плоскости 1) 3.Решить уравнение: х4+16=0 Выходной контроль Найти (каждое задание 3 балла): 1 вариант
2 вариант
Критерии оценки:
Практическое занятие № 22 Тема: Решение типовых задач на применение комплексных чисел. Цель: Научиться решать типовые задач на применение комплексных чисел Теоретические основы Комплексное число – упорядоченная пара чисел I=a+jb, Изображение синусоидальных функций времени
При расчетах цепей синусоидального тока используют символический метод расчета или метод комплексных амплитуд. В этом методе сложение двух синусоидальных токов заменяют сложением двух комплексных чисел, соответствующих этим токам. где с - модуль комплексного числа; С помощью формулы Эйлера можно перейти от показательной формы записи к алгебраической. c∙ejφ=c∙cosφ+jcsinφ a=c∙cosφ, b= c∙s От алгебраической формы записи переходят к показательной форме с помощью формул:
Комплексное число может быть представлено в виде радиус - вектора в комплексной плоскости. Вектор длиной, равной модулю c, расположен в начальный момент времени под углом φ относительно вещественной оси (рис.6.3). Умножим комплексное число на множитель
Синусоидальные функции времени могут быть представлены векторами в комплексной плоскости, вращающимися против часовой стрелки с постоянной угловой скоростью Пример.
Сложение синусоидальных токов заменим сложением комплексных амплитуд, соответствующих этим токам.
Амплитуда результирующего тока Мгновенное значение результирующего тока Законы Ома и Кирхгофа в комплексной форме:
Входной контроль. 1. Дайте определение комплексного числа
2. Перечислите различные формы записи комплексного числа 3. Как выполняется действия над комплексными числами? 4. Где в электротехнике применяются комплексные числа?
Ход работы. 1. Найти силу тока и падение напряжения на различных участках по следующим формулам: где 2. Найти силу тока и падение напряжения на различных участках по следующим формулам: где 3. Определите сопротивление
где Выходной контроль 1 вариант 1) (2 балла) Напряжение в комплексной форме описывается 2) (3 балла) Найти проводимость участка цепи, при том, что напряжение в комплексной форме описывается 3) (3 балла) Найти силу тока и падение напряжения на различных участках по следующим формулам: где 4) (3 балла) Найти силу тока и падение напряжения на различных участках по следующим формулам: где 5) (4 балла) Определите сопротивление
2 вариант 1) (2 балла) Ток в комплексной форме описывается 2) (3 балла) Найти проводимость участка цепи, при том, что напряжение в комплексной форме описывается 3) (3 балла) Найти силу тока и падение напряжения на различных участках по следующим формулам: 4) (3 балла) Найти силу тока и падение напряжения на различных участках по следующим формулам: 5) (4 балла) Определите сопротивление
Критерии оценки:
Практическое занятие № 23 Тема: Решение дифференциальных уравнений первого порядка Цель: Научиться решать дифференциальные уравнения первого порядка Теоретическая основа Уравнение, связывающее функцию y, ее аргумент x и ее производные, называется обыкновенным дифференциальным уравнением. Обыкновенное дифференциальное уравнение символически можно записать в виде
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например: А) Б) Решением дифференциального уравнения называется всякая функция y=f(x), которая, будучи подставлена в уравнение, обращает его в тождество. Процесс решения дифференциального уравнения называют интегрированием. Поэтому само решение называют еще интегралом уравнения. Определение. Общим решением дифференциального уравнения n-го порядка называется функция y=f(x, c1, c2, …, cn), зависящая от аргумента x и n произвольных постоянных c1, c2, …, cn, которая будучи подставлена в уравнение обращает его в тождество. Общее решение дифференциального уравнения называется также общим интегралом. Чтобы из общего уравнения выделить некоторое конкретное частное решение дифференциального уравнения, необходимо задать значения для параметров c1, c2, …, cn. начальному условию y(x0)=y0, получила в литературе название задачи Коши.
Дифференциальное уравнение первого порядка с разделяющимися переменными. Определение. Дифференциальное уравнение первого порядка
Разнося переменные x и y и их дифференциалы в разные стороны такого уравнения, оно может быть записано в виде
Пример Возьмем дифференциальное уравнение
Данное уравнение является с разделяющимися переменными> Разнося переменные в разные стороны, записываем уравнение в виде
Интегрирование левой и правой частей уравнения, дает общее решение вида
Как видно получилось семейство гипербол. Входной контроль. 1. Дайте определение дифференциального уравнения. 2. Что называется порядком дифференциального уравнения? 3. Чем отличается общее решение дифференциального уравнения от частного? 4. Расскажите алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными? Ход работы: 1.Найдите частное решение дифференциального уравнения при заданных начальных условиях а) ydy=(x2+sinx)dx; у=1, при х=0 б) ydy=(x3-cosx)dx; у=-1, при х=0 в) ху/=2у; у= 2, при х=3 2. Найдите общее решение дифференциального уравнения а) б) Выходной контроль: Каждое задание -1 балл 1.Найдите частное решение дифференциального уравнения
Критерии оценки:
Практическое занятие № 24 Тема: Решение дифференциальных уравнений второго порядка с постоянными коэффициентами Цель: Научиться решать дифференциальные уравнения второго порядка с постоянными коэффициентами Теоретические основы Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
y '' + py ' + qy = 0,где p и q - постоянные величины. На то, что это уравнение второго порядка, указывает наличие второй производной от искомой функции, а на его однородность - нуль в правой части. Постоянными коэффициентами называются уже упомянутые выше величины. Чтобы решить линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, нужно сначала решить так называемое характеристическое уравнение вида k ² + pq + q = 0,которое является обычным квадратным уравнением. В зависимости от решения характеристического уравнения возможны три различных варианта решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами / 1)Корни характеристического уравнения - действительные и различные (D>0) Иными словами,k1
2)Корни характеристического уравнения - действительные и одинаковые (D=0) Иными словами,k=k1=k2. В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
3)Корни характеристического уравнения – не действительные (D<0) Иными словами,k1 =
Пример. Решить линейное однородное дифференциальное уравнение y '' + y ' -2 y = 0, Решение. Характеристическое уравнение имеет вид k ² -2k -2 = 0, его корни
Пример. Решить линейное однородное дифференциальное уравнение y '' -8y' +16 y = 0, Решение. Характеристическое уравнение k ² -8k +16 = 0 имеет равные корни Общее решение данного дифференциального уравнения имеет вид Пример. Решить линейное однородное дифференциальное уравнение y '' -2y' +10 y = 0 Решение. Характеристическое уравнение k ² -2k +10 = 0 имеет комплексные корни
Соответственно Пример Найти частное решение дифференциального уравнения y '' -4 y=0, удовлетворяющее начальным условиям: y(0)=1, y|(0)=2 k ² -4k = 0 k1=-2, k2=2 Теперь нужно найти частное решение, соответствующее заданным начальным условиям. Наша задача состоит в том, чтобы найти ТАКИЕ значения констант c1, c2 чтобы выполнялись ОБА условия. Алгоритм нахождения частного решения следующий: Сначала используем начальное условие y(0)=1: y(0)= Далее берём наше общее решение
Входной контроль 1. Запишите определение дифференциального уравнения второго порядка с постоянными коэффициентами 2. Запишите характеристическое уравнение 3. Запишите решение дифференциального уравнения второго порядка с постоянными коэффициентами, если дискриминант положительный 4. Запишите решение дифференциального уравнения второго порядка с постоянными коэффициентами, если дискриминант равен нулю 5. Запишите решение дифференциального уравнения второго порядка с постоянными коэффициентами, если дискриминант отрицательный
Ход работы Найдите общее решение дифференциальных уравнений: 1) у"+3у'-4y=0 2) у"-2у'+2y=0 3) у"+у'-2y=0 4) у"-9у'=0 5) у"-у=0 Найдите частное решение дифференциальных уравнений: 1) y '' +8y' +16 y = 0; y(0)=2, y|(0)=8 2) y '' +9 y = 0; y( Выходной контроль Найдите общее решение дифференциальных уравнений (каждое задание 2 балла): Вариант 1 Вариант 2 1) у"+25у=0 1) у"+5у'=0 2) у"-3у'+2у=0 2) у"-2у'+5у=0 3) у"-9у'=0 3) у"-у=0 4)у"-6у'+9у=0 4)у"+2у'+у=0 5) у"-4у'+13у=0 5) у"+2у'+5у=0 Найдите частное решение дифференциального уравнения (4 балла): Вариант 1 Вариант 2 у||-4у|+5y=0 y '' +6y' +9 y = 0; y(0)=1, y|(0)=-1 y(0)=1, y|(0)=2 Критерии оценки:
Информационное обеспечение Основные источники: 1. Дадаян, А.А. Математика: Учебник. -М.: ФОРУМ: ИНФРА-М. 2019.- 542 с.; 2.Дадаян, А.А. Сборник задач по математике: Учебное пособие. -М.: ФОРУМ: ИНФРА-М. 2019.- 542 с.; 3.Татарников О.В. Элементы линейной алгебры. Учебник и практикум для СПО. М. – Юрайт, 2019.-334c.; 4.Попов А.М. Теория вероятностей и математическая статистика. Учебник для СПО. М. – Юрайт, 2019.-368c.;
Дополнительные источники: 1. Богомолов, Н.В. Практические занятия по математике[Текст]: Учебное пособие для средних профессиональных учебных заведений / Н.В. Богомолов. – 5-е изд., стер. - М.: Высшая школа. 2003. – 495 с. (Рекомендовано Министерством образования и науки РФ) 2. Григорьев С.Г. Математика[Текст]: учебник для студ. образоват. учреждений сред. проф. образования/С.Г.Григорьев, С.В. Иволгина; под ред. В.А. Гусева.-9-е изд., стер._М.: Издательский центр «Академия», 2013.-416 с. 3. Лапчик, М.П. Элементы численных методов [Текст]: Учебник для студентов образовательных учреждений среднего профессионального образования / М.П. Лапчик, М.И. Рагулина, Е.К. Хеннер; под ред. М.П. Лапчика. – М.: Издательский дом «Академия», 2007. – 224 с.
Интернет-ресурсы:
1. Единая коллекция Цифровых образовательных ресурсов - http://school-collection.edu.ru/ 2.Метод Гаусса, формулы Крамера, матричный определитель [Электронный ресурс]. - URL: http: // www.matburo.ru/. Дата обращения: 06.04.2011. 3.Образовательный математический сайт - http://www.exponenta.ru 4.Сайт «Теория вероятностей и математическая статистика» [Электронный ресурс]. - URL: http: // www.teorver/ru. Дата обращения: 06.04.2011. 5.Общие методы решения уравнений [Электронный ресурс]. - URL: http://www.rusedu.ru/subcat_is /htm/. Дата обращения: 06.04.2011. 6.«Дискретная математика» (журнал) [Электронный ресурс]. - URL: http: // dma.mi.ras.ru 7.«Теория вероятностей и ее применение» (журнал) [Электронный ресурс]. - URL: www.tvp.ru
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.169.223 (0.159 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 , то
, то .
. , где
, где 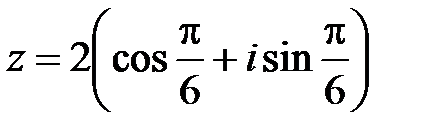 .
. , согласно формуле (2.13):
, согласно формуле (2.13):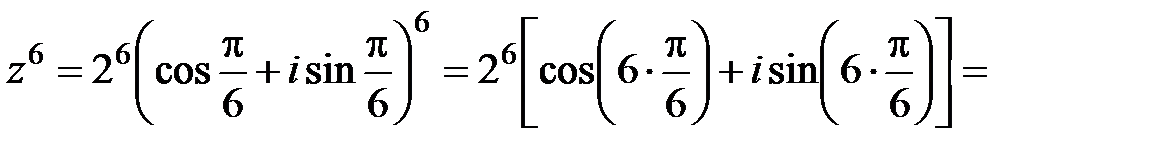
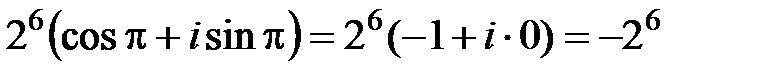 .
. N) из комплексного числа называется комплексное число, n-ая степень которого равна подкоренному числу.
N) из комплексного числа называется комплексное число, n-ая степень которого равна подкоренному числу. ,
, 
 получим n различных значений корня из комплексного числа. Следовательно, корень n–ой степени из действительного числа также имеет n комплексных значений, т.к. действительное число является частным случаем комплексного числа.
получим n различных значений корня из комплексного числа. Следовательно, корень n–ой степени из действительного числа также имеет n комплексных значений, т.к. действительное число является частным случаем комплексного числа.

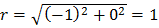 ,
, 
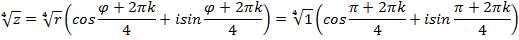


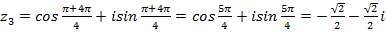


 и любого
и любого  корни степени n из числа
корни степени n из числа  -угольника с центром в нуле.
-угольника с центром в нуле.
 2)
2) 
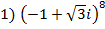 2)
2)  3)
3)  4)
4) 
 2)
2)  3)
3)  4)
4) 
 ,
, 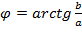
 .
. 
 , то вектор, умноженный на
, то вектор, умноженный на  , превратится во вращающийся со скоростью ω радиус - вектор.
, превратится во вращающийся со скоростью ω радиус - вектор.  называется комплексной функцией времени.
называется комплексной функцией времени. - комплексную функцию времени для напряжения.
- комплексную функцию времени для напряжения.  - комплексная амплитуда напряжения (исходное положение вектора в комплексной плоскости). Определим, чему равна мнимая часть комплексной функции времени для напряжения.
- комплексная амплитуда напряжения (исходное положение вектора в комплексной плоскости). Определим, чему равна мнимая часть комплексной функции времени для напряжения.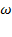 . Проекция вектора на мнимую ось изменяется по синусоидальному закону.
. Проекция вектора на мнимую ось изменяется по синусоидальному закону.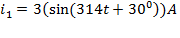 ,
, 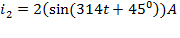

 ,
, 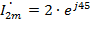

 , начальная фаза -
, начальная фаза -  .
.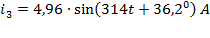
 - закон Ома;
- закон Ома; - первый закон Кирхгофа; (6.5)
- первый закон Кирхгофа; (6.5) - второй закон Кирхгофа. (6.6)
- второй закон Кирхгофа. (6.6) ,
,  ,
,  ,
,  ,
, ,
,  ,
,  ,
, 
 ,
, 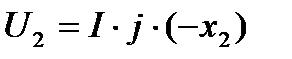 ,
,  ,
, ,
,  ,
,  ,
, 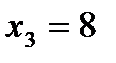
 по нижеприведенным формулам
по нижеприведенным формулам ,
, 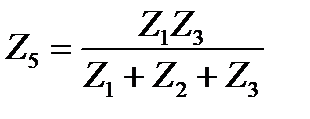 ,
, 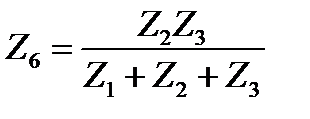 ,
, ,
,  ,
, 
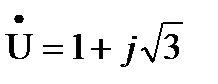 . Найти уравнение напряжения.
. Найти уравнение напряжения. .
. ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
, 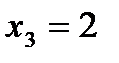
 ,
,  ,
, 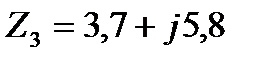
 ,
,  ,
, 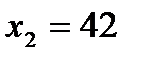 ,
, 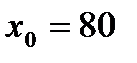
 ,
,  ,
,  ,
, 
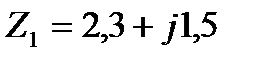 ,
, 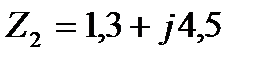 ,
, 
 или
или  .
.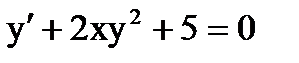 является дифференциальным уравнением 1-го порядка;
является дифференциальным уравнением 1-го порядка; является дифференциальным уравнением 2-го порядка;
является дифференциальным уравнением 2-го порядка; называется уравнением с разделяющимися переменными, если оно может быть представлено в виде
называется уравнением с разделяющимися переменными, если оно может быть представлено в виде 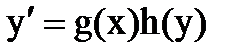 .
. (отсюда происходит название данного типа уравнения).
(отсюда происходит название данного типа уравнения). или
или  ,
, .
. , где постоянная взята в виде lnc,c>0. Далее несложно преобразовать данное уравнение к виду
, где постоянная взята в виде lnc,c>0. Далее несложно преобразовать данное уравнение к виду или
или 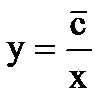 , где постоянная
, где постоянная  уже не имеет ограничений на знак.
уже не имеет ограничений на знак.


 k2. В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
k2. В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

 , k2 =
, k2 = 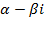 . В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
. В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
 и
и  - вещественные и различные. Общее решение данного дифференциального уравнения имеет вид
- вещественные и различные. Общее решение данного дифференциального уравнения имеет вид
 .
.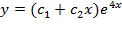

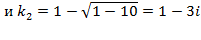
 и
и  . Общее решение данного дифференциального уравнения имеет вид
. Общее решение данного дифференциального уравнения имеет вид 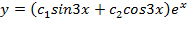


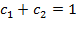



 В составленной системе удобно разделить второе уравнение на 2 и почленно сложить уравнения:
В составленной системе удобно разделить второе уравнение на 2 и почленно сложить уравнения:

 ,
, 

 -частное решение
-частное решение )=1, y|(
)=1, y|(