
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ разработанных моделей
Интерпретация коэффициентов регрессии Свободный член (сдвиг) b 0, равный в примере 1,61, формально надлежит понимать следующим образом: величина y при x1 и x2 равных 0. Однако обычно можно полагать, что в указанной совокупности исходных данных нет подобных примеров. Поэтому сдвиг b 0 следует обсуждать как вспомогательную величину, необходимую для получения оптимальных прогнозов, и не истолковывать ее столь буквально. Коэффициенты регрессии b 1 и b 2 следует рассматривать как степень влияния каждой из переменных на величину y, если все другие независимые переменные остаются неизменными. Еще раз заметим, что все названные коэффициенты регрессии отражают влияние на исследуемый параметр у только какой-то одной переменной х при непременном условии, что все другие переменные (факторы) не меняются. Ошибки прогнозирования (определение качества регрессионного анализа) Используем два приема для оценки добротности выполненного нами регрессионного анализа: − стандартную ошибку ( − коэффициент детерминации (R 2), указывающий, какой процент вариации функции у объясняется воздействием факторов хk. Рассмотрим оба подхода более подробно. Результаты статистического расчета показывают, что стандартная ошибка для функции составляет 0,65. Этот результат применительно к нашему примеру следует рассматривать следующим образом: фактическая величина y отличается от прогнозируемой не более чем на 0,65. Однако ценность этого показателя невелика, если не надежность этого утверждения. При условии сохранения нормального распределения можно полагать, что примерно 2/3 фактических данных будут находиться в пределах S Эта стандартная ошибка S
Коэффициент детерминации R 2 (на рис. 10 R -квадрат) равен 0,67, что составляет 67 %. Этот результат следует толковать так: все исследуемые воздействующие факторы объясняют 67 % вариации анализируемой функции. Остальное же 33 % остается необъясненным и может быть связано с влиянием других, неучтенных факторов. Для нашего примера показатель R 2 (67 %) считается умеренным, поэтому можно полагать, что именно эти два фактора в данном конкретном случае оказывают наиболее значительное влияние на y. Итак, нами получено уравнение множественной регрессии, коэффициенты которого b i формально показывают, как и в каком направлении действуют (вероятно) исследуемые факторы хk i и какой процент изменчивости функции у объясняется влиянием именно этих факторов. Теперь нам надлежит определить статистическую значимость полученного аналитического выражения. Проверка значимости модели При проверке значимости модели принято придерживаться следующей последовательности действий: 1. Сначала выполняется общая проверка полученного уравнения на пригодность. 2. Если результат оказался положительным (уравнение значимо), то проверяют на значимость уже каждый коэффициент уравнения регрессии bi. 3. Дается сравнительная оценка степени влияния каждого из анализируемых факторов хk. Проверка на адекватность уравнения регрессии Статистическую оценку полученного уравнения (так называемый статистический вывод) принято начинать с проведения F -теста, целью которого является выяснение способности исследуемых факторов хk объяснять значимую часть колебания функции у. Этот тест используется как своеобразные «входные ворота» в статистический вывод: если результат теста значим, то связь существует, значит можно приступать к ее исследованию и объяснению. Если проверка указывает на незначимость связи, то заключение лишь одно: мы имеем дело с набором случайных чисел, никак не связанных между собой. И больше делать нечего, так как нет предмета для анализа.
Сам формальный факт отсутствия значимости на деле может и не соответствовать отсутствию взаимосвязи как таковой. Просто в указанных обстоятельствах у нас не хватило экспериментальных данных доказать, что такая связь вообще-то есть. Иначе говоря, она может и быть, но из-за малого размера выборки или какой-либо случайности нам не удалось ее доказать на основании тех опытных данных, которые были в нашем распоряжении. Использование так называемой нулевой гипотезы для F -теста означает, что между переменными хk и у значимая связь отсутствует. Следовательно, признается, что параметр у является чисто случайной величиной, поэтому значения переменных хk не оказывают на него никакого систематического влияния. Применительно к уравнению регрессии — это утверждение можно трактовать как случай, когда все коэффициенты уравнения равны нулю. С другой стороны, альтернативная гипотеза F -теста говорит о том, что между параметром у и переменными хk существует определенная прогнозирующая взаимосвязь. Следовательно, параметр у уже не является чисто случайной величиной и должен зависеть хотя бы от одной из переменных хk. Тем самым альтернативная гипотеза настаивает на том, что по крайней мере один из коэффициентов регрессии отличен от нуля. Как видно, здесь принимается во внимание следующее обстоятельство: совершенно необязательно, чтобы каждая х -переменная влияла на параметр у, вполне достаточно, чтобы влияла хотя бы одна из них. Для выполнения F -теста воспользуемся результатами компьютерного расчета, который исполнил Excel. Здесь обычно рекомендуются следующие приемы. 1. Решение принимается на основе критерия Фишера. F -тест проводится путем сопоставления вычисленного значения F -критерия с эталонным (табличным) показателем F табл для соответствующего уровня значимости. Если выполняется неравенство F расч<Fтабл, то с уверенностью, например, на 95 %, можно утверждать, что рассматриваемая зависимость у = b 0 + b 1 x 1 + b 2 x 2 +…+ bkxk является статистически значимой. В противном случае – наоборот. 2. Решение принимается на основе уровня значимости α (в интерпретации Excel это показатель р). Если р -значение больше, чем 0,05, то полученный результат нужно трактовать как незначимый (для 95 %-й вероятности). В том случае, когда величина р оказывается меньше 0,05, то вывод такой: это значимое уравнение с вероятностью 95 %. Если же р <0,01, то полученный результат является высоко значимым, (степень риска ошибиться в нашем утверждении оказывается меньше 1 %, т.е. степень надежности составляет 99 %) 3. Решение принимается на основе коэффициента детерминации R2. В этом случае имеющуюся расчетную величину R 2расч (см. рис. 10) необходимо сравнить с табличными (критическими) значениями R 2крит для соответствующего уровня значимости (повторим еще раз, обычно это 0,05). Если окажется, что R 2расч> R 2крит, то с упомянутой степенью вероятности (95 %) можно утверждать, что анализируемая регрессия является значимой. Пример Проанализируем полученное выше уравнение регрессии с использованием рассмотренных статистических критериев. Проверка по F-критерию. Компьютерный расчет выдал величину F расч, равную 16,99 (см. рис.10). Для анализа уравнения будем пользоваться величиной F расч, обратной представленной Excel. Она составит 1:16,99 = = 0,06. Отыщем по эталонной таблице (прил. Д) критическую величину F крит при условии, что для числителя степень свободы f 1 = k, т.е. составит 2 (число воздействующих факторов равно 2), а для знаменателя
f 2 = n − k −1 = 20 − 2 − 1= 17. Тогда будем иметь следующие значения для F крит: 3,6 (для α = 0,05), 6,2 (α = 0,01) и 10,5 (α = 0,001). Понятно, что для всех рассмотренных вероятностей выполняется соотношение F расч<Fкрит, поэтому уверенно можно говорить о высокой степени адекватности анализируемого уравнения. Проверку с использованием уровня значимости α (в Excel этот показатель именует как р). На рис.10 находим позицию «Значимость F». Там указана величина 8,84Е-5, т.е. это число 8,84, перед которым стоит 5 нулей. Фактически можно признать, что α = 0,000. Это говорит о том, что действительно обнаруживается устойчивая зависимость рассматриваемой функции у от воздействующих факторов х 1 и х 2, т.е. y не является чисто случайной величиной. Но пока неизвестно, какие именно факторы (оба х 1 и х 2или какой-то один из них) реально участвует в прогнозировании, но доподлинно понятно, что по крайней мере один из них влияет непременно. Проверка по коэффициенту детерминации R 2. По расчетам, коэффициент детерминации R 2расч составляет 0,67, или 67 %. Таблица для тестирования на уровне значимости 5 % в случае выборки n = 20 и числа переменных k = 2 дает критическое значение R 2крит = 0,297 (прил. Е). Поскольку выполняется соотношение R 2расч> R 2крит, то с вероятностью 95 % можно утверждать о наличии значимости данного уравнения регрессии. Кстати заметим, что для наших обстоятельств (n = 20, k = 2) можно оценить критическое значение R 2крит для α = 0,01 (высокая значимость) и α = 0,001 (высшая степень значимости). В этом случае R 2крит составляет соответственно 0,384 и 0,517, что, как видно, все равно остается меньше расчетного показателя R 2расч, т.е. 0,67. Из чего следует заключить, что обсуждаемое нами уравнение действительно характеризуется очень высокой степенью значимости. Как видно, все три рассмотренных приема статистической проверки дают одинаковый результат. В этом примере мы воспользовались подобным разнообразием способов анализа только с одной целью – дать представление о существующих методах такой проверки. На практике наиболее распространенным методом считается выполнение проверки по F -критерию. Итак, проведена проверка на значимость самого уравнения, т.е. установлено, что существует взаимосвязь между параметром у и переменными хk. Однако нам пока неясно, каково влияние конкретных факторов х 1 и х 2 на исследуемую функцию у: действуют ли оба фактора или только какой-то один из них. Поэтому предстоит определить значимость отдельных коэффициентов регрессии b 1 и b 2. Для этой цели используется так называемый t- тест.
Проверка на адекватность коэффициентов регрессии Проверку на адекватность коэффициентов регрессии рекомендуется проводить по следующим эквивалентным методам. Использование t-критерия. Необходимые расчеты делает Excel, который выдает значения показателя t. Анализируемый коэффициент считается значимым, если его t-критерий по абсолютной величине превышает 1,96, что соответствует уровню значимости 0,05 (табл. 3). В нашем примере имеем для коэффициентов b 0, b 1 и b 2 следующие показатели критерия Стьюдента: tb 0 = 2,09; tb 1 = 2,59 и tb 2 = 2,57. Из всего вышесказанного следует, что значимыми оказываются все коэффициенты нашегоуравнения. Использование уровня значимости. В этом случае оценка проводится путем анализа показателя р, т.е. уровня значимости α. Коэффициент признается значимым, если рассчитанное для него р -значение (эти данные выдает Excel) меньше (или равно) 0,05 (т.е. для 95 %-й доверительной вероятности). Показатель р составляет для коэффициентов b 0, b 1 и b 2 следующие величины: р b 0 =0,05; р b 1=0,02 и р b 2 =0,02. Эти данные позволяют также заключить, что все рассмотренные коэффициенты статистически значимы. Иначе говоря, можно сделать вывод о неслучайном характере влияния всех изученных параметров. Таким образом, проверка обоими методами дает вполне согласованные результаты. Поэтому в окончательном виде наше уравнение регрессии (для уровня значимости 0,05) следует записать так ŷ = 1,61 + 0,06 x 1 + 0,07 x 2. Сравнительная оценка степени влияния факторов Для решения данной задачи используем метод сравнения стандартизованных коэффициентов регрессии. В общем случае все коэффициенты регрессии b 1, b 2, …, bk могут быть выражены в разных единицах измерения. Тем самым непосредственное их сравнение становится фактически некорректным, поскольку формально меньший по величине коэффициент на деле может оказаться важнее большего. Стандартизованные коэффициенты регрессии позволяют решить эту проблему за счет представления коэффициентов регрессии в некоторых кодированных единицах измерения. Стандартизованный коэффициент регрессии вычисляется путем умножения коэффициента регрессии bi на стандартное отклонение Sn (для х -переменных обозначим его как Sxk) и деления полученного произведения на Sу. Это означает, что каждый стандартизованный коэффициент регрессии измеряется как величина bi Sxk / Sу. Применительно к нашему примеру получим следующие результаты (табл. 6).
Таблица 6 Стандартизованные коэффициенты регрессии
После проделанных расчетов мы можем на объективном основании сопоставить полученные коэффициенты. Для обоих анализируемых факторов стандартизованные коэффициенты практически одинаковы. Таким образом, приведенное сравнение абсолютных величин стандартизованных коэффициентов регрессии позволяет получить наглядное представление о важности рассматриваемых факторов. Еще раз напомним, что эти результаты не являются идеальными, поскольку не в полной мере отражают реальное влияние исследуемых переменных (мы оставляем без внимания факт возможного взаимодействия этих факторов, что может исказить первоначальную картину). В целом же проведенный регрессионный анализ дает основание оценить влияние рассмотренных факторов на функцию. Вместе с тем ставятся задачи на доработку модели: явно неприняты во внимание все факторы (33 % приходится на неучтенные причины). Заключение В заключении курсовой работы необходимо кратко отразить качественные и количественные результаты выполненной работы. Отразить положительные и отрицательные моменты и привести рекомендации по устранению недостатков.
Список рекомендуемой литературы 1. Ратнер С.В., Киселева Н.В. Программные статистические комплексы в менеджменте качества: учеб. пособие. Краснодар: Кубан. гос. ун-т, 2011. 185 с. 2. Барботько А. И. Основы теории математического моделирования: учеб. пособие для студ. вузов, обуч. по напр. «Конструкторско-технологическое обеспечение машиностроительных производств» / А.И. Барботько [и др.]. Старый Оскол: ТНТ, 2013. 212 с. 3. Зарубин В. С. Математическое моделирование в технике: учебник для студентов высших технических учебных заведений. – Изд. 3-е. М.: Изд-во МГТУ им. Н. Э. Баумана, 2010. 496 с. 4. Казаков Ю.М., Аверченков В.И. Автоматизация проектирования технологических процессов: учеб. пособие для вузов. М.: ФЛИНТА, 2011. 229 с. 5. Моделирование систем: учебник рек. Мин. обр. РФ / С. И. Дворецкий [и др.]. М.: Академия, 2009. 317 с. 6. Шаламов В.Г. Математическое моделирование при резании металлов: учеб. пособие. Челябинск: Изд-во ЮУрГУ, 2007. 134 с. Приложение А
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-14; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.184.117 (0.045 с.) |
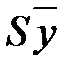 ), которая дает представление о приблизительной величине ошибки прогнозирования;
), которая дает представление о приблизительной величине ошибки прогнозирования; от прогнозируемой; примерно 95 % − в пределах 2 S ⎯ у и т.д.
от прогнозируемой; примерно 95 % − в пределах 2 S ⎯ у и т.д.


