Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логическая операция ИНВЕРСИЯСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
· соответствует частице НЕ; · обозначается черточкой над именем переменной; · иначе называется ОТРИЦАНИЕ. Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
Операция логического сложения (дизъюнкция) Соединение двух высказываний А и В в одно с помощью союза “ИЛИ”, употребляемого в неисключающем смысле, называется логическим сложением (дизъюнкцией), а полученное составное высказывание - логической суммой. Дизъюнкция обозначается знаком “+” или знаком “ Ú“ (А + В или АÚ В) Логическая операция дизъюнкция · соответствует союзу ИЛИ; · обозначается знаком Ú или +, · иначе называется ЛОГИЧЕСКОЕ СЛОЖЕНИЕ. Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны.
Операция логического умножения (конъюнкция) Соединение двух высказываний А и В в одно с помощью союза “И”, называется логическим умножением (конъюнкцией). Логическая операция КОНЪЮНКЦИЯ · соответствует союзу И; · обозначается знаком Ù или ·; · иначе называется ЛОГИЧЕСКОЕ УМНОЖЕНИЕ. Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания истинны.
Импликация. Логическая операция, соответствующая союзу “если..., то...” называется импликацией. Логическая операция ИМПЛИКАЦИЯ · соответствует союзу ЕСЛИ..., ТО...; · обозначается знаком ®. Импликация высказываний ложна лишь в случае, когда А истинно, а В ложно.
Эквиваленция. Логическая операция, соответствующая союзу “тогда и только тогда, когда” называется эквиваленцией. Логическая операция ЭКВИВАЛЕНЦИЯ · соответствует союзу ТОГДА И ТОЛЬКО ТОГДА, КОГДА...; · обозначается знаком «. Эквиваленция двух высказываний истинна в том и только в том случае, когда оба эти высказывания истинны или оба ложны.
Пример. Задания и упражнения. 1. Даны простые высказывания: 2. Даны простые высказывания: 3. Прочтите формулы: 4. В состав истинного логического произведения входят три простых высказывания - A,B,C. Известно, что A и B - истинны. Может ли высказывание C быть одним из следующих: а) “Дважды два равно семи”. 5. Дано высказывание: “Иванов является членом сборной команды “Алгоритм”. Какое из следующих высказываний есть логическим отрицанием данного? 6. Определите значения истинности высказываний: Таблицы истинности Таблица истинности - это таблица, устанавливающая соответствие между всеми возможными наборами логических переменных, входящих в логическую функцию и значениями функции. Таблицы истинности применяются для:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1464; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.247.50 (0.01 с.) |



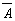 · В·
· В· 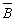 · С
· С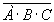
 3).
3).