Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
VII. Дифференциальные уравнения
Основные понятия
Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции. Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным, если от нескольких – то уравнением в частных производных. Мы будем рассматривать только обыкновенные дифференциальные уравнения (и по этой причине само слово “обыкновенные” будем опускать). В общем случае дифференциальное уравнение можно записывать в виде:
при этом порядок Решением дифференциального уравнения (7.1) называется такая функция График решения дифференциального уравнения называется интегральной кривой. Общим решением дифференциального уравнения (7.1)
которое является фукцией переменной Частным решение дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных К дифференциальным уравнениям приводят ряд задач экономики, физики, биологии, экологии и т.п.
Дифференциальные уравнения первого порядка v Уравнение с разделяющимися переменными. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде:
или в виде:
где Для решения такого уравнения его следует преобразовать к виду, в котором дифференциал и функции переменной Пример 1. Решить уравнение.
Решение.
v Однородные дифференциальные уравнения. Диффернциальное уравнение первого порядка называется однородным, если оно может быть представленно в виде:
где Понятие однородного дифференциального уравнения связано с однородными функциями. Функция
Однородные уравнения при помощи подстановки Пример. Решить уравнение: Решение. Так как
Получим уравнение с разделяющимися переменными:
Интегрируя почленно последнее равенство, получаем:
Возвращаясь к первоначальным переменным, получим:
v Линейные дифференциальные уравнения. Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид:
где Рассмотрим один из возможных способов решения уравнения: будем искать решение в виде Пример. Решить уравнение: Решение. Разделив левую и правую части на
Пусть
Пользуясь тем, что одну из вспомогательных функций (например
Проинтегрировав, найдем какое-либо частное решение этого уравнения, например, при При
Решая это уравнение с разделяющимися переменными, получаем
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 264; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.91.37 (0.013 с.) |
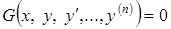 (7.1)
(7.1) старшей производной, входящей в запись уравнения, называется порядком дифференциального уравнения.
старшей производной, входящей в запись уравнения, называется порядком дифференциального уравнения.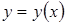 , которая при подстановке ее в это уравнение обращает его в тождество.
, которая при подстановке ее в это уравнение обращает его в тождество.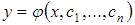 (7.2)
(7.2) и
и 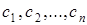 . (Независимость постоянных означает отсутствие каких-либо соотношений между ними).
. (Независимость постоянных означает отсутствие каких-либо соотношений между ними).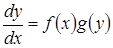 (7.3)
(7.3)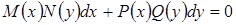 (7.4)
(7.4)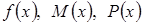 - некоторые функции переменной
- некоторые функции переменной 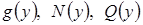 - функции переменной
- функции переменной  .
.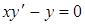
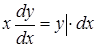 ;
;  ;
; 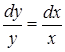 ;
;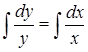 ;
;  ;
; 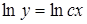 ;
; 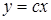 .
.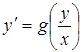 (7.5)
(7.5)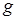 - некоторая функция (одной переменной).
- некоторая функция (одной переменной).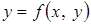 называется однородной степени
называется однородной степени 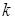 (по переменным
(по переменным  выполняется равенство:
выполняется равенство: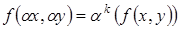 (7.6)
(7.6)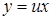 приводятся к уравнениям с разделяющимися переменными.
приводятся к уравнениям с разделяющимися переменными. .
.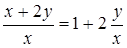 , то уравнение имеет вид (7.5) при
, то уравнение имеет вид (7.5) при 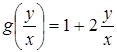 . Положим
. Положим  , отсюда
, отсюда 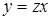 и
и 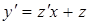 . Подставим в преобразованное уравнение:
. Подставим в преобразованное уравнение: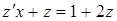 ,
, .
.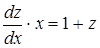 ,
, .
.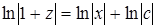 ,
,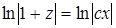 ,
,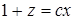 .
.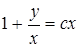 , откуда
, откуда 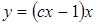 .
.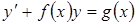 (7.7)
(7.7) и
и 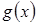 - некоторые (непрерывные) функции переменной
- некоторые (непрерывные) функции переменной 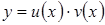 , тем самым искомыми становятся функции
, тем самым искомыми становятся функции 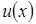 и
и  , одна из которых может быть выбрана произвольно, а другая – должна определяться из уравнения (7.7). Т.е. используется в решении замена
, одна из которых может быть выбрана произвольно, а другая – должна определяться из уравнения (7.7). Т.е. используется в решении замена 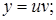
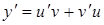 .
. .
.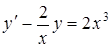 .
.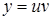 ,
, 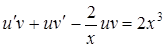 или
или 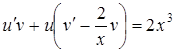 .
. ) можно выбрать произвольно, подберем ее так, чтобы выражение в скобках обратилось в нуль, т.е. в качестве
) можно выбрать произвольно, подберем ее так, чтобы выражение в скобках обратилось в нуль, т.е. в качестве 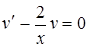 или
или  откуда
откуда 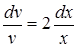 .
.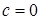
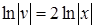 и
и 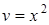 .
.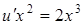 или
или 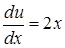 .
.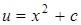 . Тогда окончательно имеем:
. Тогда окончательно имеем: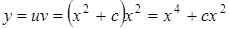 .
.