Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальность и равновесность состояний
Зная, что равновесное состояние модели может быть или не быть оптимальным по Парето, также как и Парето-оптимальное состояние может быть или не быть равновесным в заранее определенном смысле, рассмотрим связи между равновесным состоянием (6.10) — (6.13) и оптимальными состояниями в смысле глобальных критериев WI и WII, соизмеряющих уровни удовлетворения групп от их потребления и трудовой деятельности. Оказывается, в рамках определенных, не очень жестких условий, накладываемых на соотношения модели (6.1) — (6.6), между ними существует строгое соответствие. Эти условия сводятся к следующим требованиям. (I) Интервальные функции полезности ui(xi, li), определенные на векторах (II) Множество технологических возможностей производства - множество пар (III) Все коэффициенты (IV) Область, определенная соотношениями (6.1) — (6.5), ограничена. (V) Выполняется условие Слейтера, т. е. существуют такие допустимые векторы /i', /', хi', у', i = 1, 2,..., n, что Очевидно, в этих условиях задачи на максимум выпуклых функционалов WI или WII имеют оптимальные решения, совпадающие с соответствующей компонентой седловой точки функции Лагранжа. С учетом всего изложенного могут быть сформулированы следующие четыре теоремы. Теорема 4. Всякому оптимальному решению {хi°, li°}1n, y°, l° задачи на максимум функции WI при ограничениях (6.1) — (6.5) соответствуют такие векторы оценок р° q° и величины трансфертов Ц°, что все они в совокупности образуют равновесие вида (6.10) — (6.13). Пусть, далее, набор векторов {хi°, li°}, y°, l° образует оптимальное решение в задаче на max min iui(xi, li) при прежних ограничениях. Рассмотрим оптимизационную задачу с критерием WII = minl iui(xi, li), l i > 0, представив ее в виде:
Пусть хi°, li°, y°, l° образуют ее оптимальное решение, a Теорема 5. Если при выполнении условий (I) — (V) в задаче (6.14) — (5.17) оптимальные оценки Две следующие теоремы обратны предыдущим. Теорема 6. Пусть в условиях (I) — (IV) набор р*, q*, {xi*, li*}, у*, l *, {Di*} образует такое равновесие, при котором каждая группа имеет ненулевое потребление хотя бы одного продукта. Тогда существует единственный набор величин
Теорема 7. Пусть в тех же условиях, что и для теоремы 6, набор р*, q*, у*, l*, {xi*, li* Di*} образует равновесие. Пусть также "масштаб измерения интервальных полезностей ui выбран так, что ui(xi*, li*) = иi* > О V i. Тогда существуют такие коэффициенты Отметим, что теоремы 5 и 7 говорят о несколько разных оптимальных состояниях задачи с критерием WII. Теорема 5 гарантирует равновесность оптимального состояния только при строгой положительности оценок Совпадение равновесия с оптимумом означает, что каждое состояние народного хозяйства, отвечающее принятому критерию оптимальности, оказывается выгодным с точки зрения каждой группы и экономики в целом, если доходы и оценки определяются как двойственные переменные задачи оптимизации плана. Изменение внешних условий должно сопровождаться переходом экономики в новое состояние, которое также будет выгодным для групп при новых ценах и оценках. Равновесие (6.10) — (6.13) представляет собой некоторую нормативную модель возможных экономических взаимоотношений и, разумеется, не имеет прямого аналога в действительности. Однако если считать, что некоторая реальная экономическая система находится в оптимальном состоянии по отношению к функционалам W, WI или WII - то это означает, что равновесие как бы присутствует «в скрытой форме».
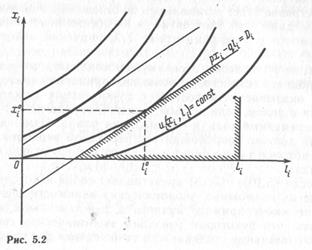
С точки зрения практической осуществимости важны не сами равновесные состояния, а, как это отмечалось в гл. 4, процессы взаимодействия всех участников экономической системы. Равновесное состояние должно быть «стационарным» по отношению к такого рода процессам. Определенный интерес представляют соотношения (6.11). Если величина Di0 для группы i строго положительна (см. рис. 6.2), то это означает, что к суммарной оценке трудозатрат группы дополнительно прибавляется некоторая величина, увеличивающая ее возможности как потребителя. Если Di0 <0, то из общей оценки трудозатрат вычитается некоторая величина, и, хотя оптимальное состояние (xi0; li0) — наилучшее для группы с точки зрения ее целевой функции и ее возможностей, все же могут существовать точки, являющиеся выпуклой линейной комбинацией данной точки и точки (0,0), более выгодные, чем оптимальная, и не удовлетворяющие ограничениям модели поведения (6.11). Подобная ситуация может показаться некоторым нарушением «суверенитета» группы как потребителя, которая, может быть, предпочла бы в течение данного промежутка времени частично «ничего не делать и ничего не получать», а частично иметь возможность получать xi0 в обмен на трудозатраты li0. Однако такая интерпретация неправомочна, поскольку трудозатраты оцениваются именно за весь данный промежуток времени, рассматриваемый как единичный.
Главной особенностью модели равновесия (6.10) —(6.13) является наличие трансфертов Df, которые участвуют в формировании дохода групп и которые можно интерпретировать как разбиения общей прибыли и ренты (за вычетом определенной «общеэкономической нагрузки») между группами. В принципе можно было бы организовать разбиение величины D* = (р*, у—a) — (q*, /) по некоторому жесткому правилу, например, зафиксировав «долевое» участие групп в виде коэффициентов аi (как это фактически делается в модели Эрроу — Дебре). Можно также задать некоторое априорное правило, устанавливающее значения трансфертов Di* в зависимости от общей суммы D, а также цен p* и оценок q*: Di = Di[D, p, q], D = SDi. Такое правило тогда выражало бы принципы распределения данной экономической системы, поскольку указывало бы для каждой группы максимально допустимую разность между оценкой потребления группы и оценкой ее трудового вклада. Достоинством равновесного механизма функционирования является то, что хозяйство СЭО, без дополнительного решения в неком «центре» глобальной задачи на оптимизацию, сохраняет состояние, «выгодное» всем участникам данного экономического процесса. Однако с точки зрения непосредственного соотношения уровней удовлетворения потребностей схемы равновесия имеют существенный дефект, на который почему-то обращается мало внимания. Даже если равновесный механизм «выводит» экономику в оптимальное состояние, соответствующий способ согласования, определяемый ценами р* и оценками q*, зависит от «внешней среды», т.е. оказывается неинвариантным. В классической модели Эрроу — Дебре [19, 32] доход потребителя i зависит от постоянной доли в прибыли производства. При разных внешних условиях равновесные состояния хотя и будут оптимальными в смысле функционалов
Было бы очень удобно, если бы принятые принципы согласования допускали одновременно свое выражение и в форме задания весовых коэффициентов Однако это не так. Действительно, зафиксировав коэффициенты Можно, конечно, считать, что изменения оценок отражают объективные условия, в которых находится экономика, а это должно находить отражение и в изменении соотношения между уровнями удовлетворения, однако трудно принять, что принципы согласования надо задавать в неких оценках, а не непосредственно в воспринимаемых потребителями показателях. С точки зрения участника процесса производства, его труд остается самим собой, как и то, что он потребляет, независимо от степени дефицитности того или иного фактора в данной системе. Поэтому естественно ожидать определенных «гарантий» по сохранению неизменными принципов соизмерения. Но тогда параметры, задающие распределение в равновесном функционировании, должны каким-то образом меняться. В данном случае это означает неизменность коэффициентов Как мы видим, с точки зрения отражения принятых принципов распределения в моделях социально-экономического планирования оптимальный подход представляется более строгим и адекватным. Однако в этом случае возникает задача формирования и корректировки параметров равновесия, поддерживающих в качестве «обратной связи» оптимум. Рассмотрим эту задачу на совсем простом примере, который позволит более ясно выразить основные аспекты всей проблемы.
Пусть анализируемая система состоит из двух подсистем двух групп потребителей, каждая из которых использует один и тот же вид ресурса в объеме sk («деньги»), максимизируя уровень удовлетворения своих потребностей, потребляя набор продуктов по ценам р: u1(х1) х1 Система в целом пусть располагает общим объемом распределяемого ресурса s, так что имеет место s1 + s2 = S. (6.30) Состоянием системы естественно считать пару векторов xl и x2, удовлетворяющих (5.29). Если задан «принцип распределения» суммарного дохода между потребителями, например, в виде а = а(р, s), так что 0 < а(р, s) < 1, s1 = aS, s2=(l — a)S, то этим задано равновесное функционирование; при изменении «внешней среды» (цен р и дохода S) система будет приходить в равновесие путем независимых частных оптимизаций. Но можно предположить, что существует глобальный критерий оптимальности, соизмеряющий интересы с помощью весовых коэффициентов
xl, х2 Необходимо установить, какова связь между равновесным состоянием ( Рассмотрим задачу такого формирования экономических параметров (в данном случае доходов участников), которое при изменении внешних условий (в нашем случае общего дохода S и цен р) будет неизменно соответствовать принятым принципам согласования. Нетрудно убедиться, что если сформулировать равновесие для данного оптимального плана (
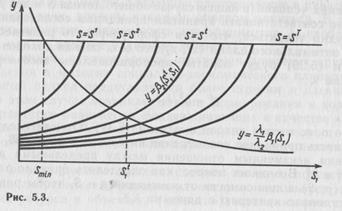
где Положим сначала, что p=const, а для разных значений S
(на рис. 5.3 приводится номограмма, позволяющая находить распределение общего дохода S на части s1 и s2 в соответствии с весовыми коэффициентами
Чтобы найти распределение доходов в случае изменения цен и при числе участников больше двух, необходимо предварительно рассчитать все функции Далее решается система уравнений:
Выразив величины si (при данных ценах) через s1 : si = подставив их выражения в (6.32), можно определить s1; затем по формулам (6.34) определяются и остальные si. Таким образом, можно представить себе механизм равновесно-оптимального функционирования: сначала определяются принципы учета потребительских интересов всех участников, выражаемые набором коэффициентов
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.239.231 (0.038 с.) |
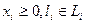 , строго выпуклы по xi, li, непрерывно дифференцируемы и
, строго выпуклы по xi, li, непрерывно дифференцируемы и 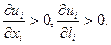
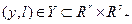 - векторов строго выпукло.
- векторов строго выпукло. положительны и
положительны и 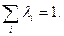
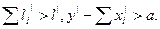
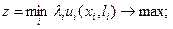 (6.14)
(6.14)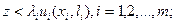 (6.15)
(6.15)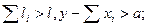 (6.16)
(6.16)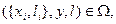 т. е.
т. е. 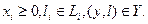 (6.17)
(6.17)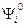 , p°, q° суть двойственные оценки, соответствующие ограничениям (6.15) и (6.16). Тогда имеет место следующая теорема.
, p°, q° суть двойственные оценки, соответствующие ограничениям (6.15) и (6.16). Тогда имеет место следующая теорема.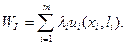
 достигает максимума на равновесных состояниях у*, l *, {xi*, li*} при ограничениях (6.16) — (6.17).
достигает максимума на равновесных состояниях у*, l *, {xi*, li*} при ограничениях (6.16) — (6.17). — значения переменных, удовлетворяющих условиям (6.16) — (6.17)}. Теорема 7 утверждает, что всякое равновесное состояние будет оптимальным по отношению к целевому функционалу WII, даже если этот оптимум не обеспечивает строгой пропорциональности с коэффициентами 1/ l i, значений целевых функций ui.
— значения переменных, удовлетворяющих условиям (6.16) — (6.17)}. Теорема 7 утверждает, что всякое равновесное состояние будет оптимальным по отношению к целевому функционалу WII, даже если этот оптимум не обеспечивает строгой пропорциональности с коэффициентами 1/ l i, значений целевых функций ui.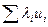 , но коэффициенты
, но коэффициенты 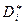 (например, с помощью некоторых функций Di (D, p, q), то соответствующее равновесное состояние будет оптимальным с вполне определенными коэффициентами
(например, с помощью некоторых функций Di (D, p, q), то соответствующее равновесное состояние будет оптимальным с вполне определенными коэффициентами 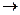 max, u2(х2)
max, u2(х2) 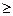 0, (р, х1 )
0, (р, х1 ) 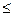 s1 ; х2
s1 ; х2 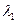 и
и 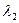 . Тогда состояние системы определяется решением следующей экстремальной задачи выбора:
. Тогда состояние системы определяется решением следующей экстремальной задачи выбора: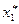 ,
, 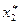 ) модели (5.29) — (5.30) и оптимальным состоянием (
) модели (5.29) — (5.30) и оптимальным состоянием (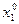 ,
, 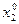 ) модели (5.31). Как легко видеть, каждое оптимальное состояние (при некоторых естественных предложениях относительно функций ui) будет равновесным состоянием, если
) модели (5.31). Как легко видеть, каждое оптимальное состояние (при некоторых естественных предложениях относительно функций ui) будет равновесным состоянием, если 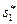 = (р,
= (р, 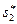 = (р,
= (р, 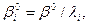
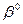 — о. о. оценка дохода в модели (6.31). Отсюда следует, что неизменность принципов соизмерения интересов в форме Wl требует сохранения неизменным отношения между предельными полезностями
— о. о. оценка дохода в модели (6.31). Отсюда следует, что неизменность принципов соизмерения интересов в форме Wl требует сохранения неизменным отношения между предельными полезностями 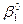 и
и 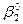 . Возникает вопрос: как определять правило распределения а (р, S) в зависимости от изменений р и S, чтобы равновесие соответствовало критерию с данными
. Возникает вопрос: как определять правило распределения а (р, S) в зависимости от изменений р и S, чтобы равновесие соответствовало критерию с данными 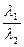
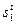 определяет доход первой группы потребителей, а доход второй будет соответственно равен
определяет доход первой группы потребителей, а доход второй будет соответственно равен  = St —
= St — 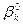 =
= 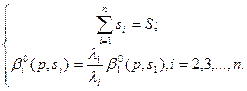 (6.32), (6.33)
(6.32), (6.33)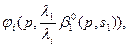 (6.34)
(6.34)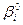 =
=  , р°,). После этого ими же решается система уравнений (6.32)—(6.33), в результате чего будет найдено распределение общего дохода S между всеми потребителями.
, р°,). После этого ими же решается система уравнений (6.32)—(6.33), в результате чего будет найдено распределение общего дохода S между всеми потребителями.