Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисления с помощью двойного интеграла.
1. Объем. Напомним, что объем V тела, ограниченного сверху поверхностью z = f(x, y)(f(x, y) ³ 0), снизу – плоскостью z = 0, а сбоку – цилиндрической поверхностью, направляющей для которой служит граница области D, а образующая параллельна оси Oz, определится соотношением
1.1. Если тело ограничено сверху поверхностью z = f1(x, y) ³ 0, снизу – поверхностью z = f2(x, y) ³ 0, причем проекцией обеих поверхностей на плоскость хОу является область D, то объем V этого тела равен разности объемов двух цилиндрических тел: оба имеют нижним основанием область D, а верхним – поверхности z = f1(x, y) ³ 0 для первого и z = f2(x, y) ³ 0 для второго,
Формула (7.10) верна и тогда, когда f1(x, y) и f2(x, y) – любые непрерывные функции, удовлетворяющие неравенству f1(x, y) ³ f2(x, y). 1.2. Если в области D функция f(x, y) меняет знак, то следует разбить область на две части: D1, где f(x, y) ³ 0 и D2, где f(x, y) £ 0. Если области D1 и D2 таковы, что двойные интегралы по ним существуют, то первый будет равен объему тела, лежащего выше плоскости хОу, а второй – объему тела, лежащего ниже плоскости хОу. 2. Площадь плоской области. Площадь области D в плоскости хОу численно равна объему рассмотренного цилиндра, ограниченного сверху в нашем случае поверхностью z = f(x, y) = 1, т.е. 3. Площадь поверхности, заданной уравнением z = f(x, y) и ограниченной некоторой замкнутой линией С. Проекцию этой линии на плоскость хОу обозначим через L, а область, ограниченную линией L, обозначим через D. Если функция f(x, y) непрерывна и имеет непрерывные частные производные в этой замкнутой области, то искомая площадь поверхности определится выражением С помощью двойного интеграла можно решить и целый ряд “физических” задач: вычисление массы плоских пластин с известной поверхностной плотностью r = f(x, y), момента инерции плоской фигуры и т.д. Тройной интеграл. Пусть в декартовых трехмерных координатах задана «объемная» область V, ограниченная замкнутой поверхностью S и пусть в каждой точке этой области, включая границу, определена непрерывная функция f(x, y, z). Разобьем область V произвольным образом на малые области (объемы) DVi, выберем в каждой произвольную точку Рi(xi, yi, zi) и составим интегральную сумму вида
где dxdydz = dV элемент объема в декартовых координатах. Если f(x, y, z) ³ 0 описывает плотность распределения вещества в объеме V, то (7.13) даст массу этого вещества. Если: 1. Всякая прямая, параллельная оси Оz и проходящая через внутреннюю точку области V, пересекает поверхность S в двух точках; 2. Область V проектируется на плоскость хОу в правильную двумерную область D; 3. всякая часть области V, отсеченная плоскостью, параллельной одной из координатных обладает свойствами 1. и 2. – область V называют правильной. Введем понятие трехкратного интеграла Iv по области V от функции f(x, y, z) определенной и непрерывной в этой области. Пусть z = y1(x,y) и z = y2(x,y) уравнения поверхностей, ограничивающиx область V снизу и сверху (вместе они описывают замкнутую поверхность S), а область D – проекция V на плоскость xОу – ограничена линиями у = j1(х), у = j2(х), х = а, x = b. Трехкратный интеграл Iv определяется выражением:
При интегрировании по z переменные х и у считаем постоянными. После интегрирования по z и подстановки пределов получаем двукратный интеграл, рассмотренный в предыдущем разделе. Трехкратный интеграл обладает свойствами, аналогичными свойствам двукратного: 1. Если область V разбить на две областии V1 и V2 плоскостью, параллельной одной из координатных, то трехкратный интеграл по области V равен сумме трехкратных интегралов по областям V1 и V2. (При любом разбиении области V на конечное число V1, V2, …,Vn плоскостями, параллельными координатным, справедливо равенство: IV = IV1+ I V2+ … +IVn). 2. Если m и М – наименьшее и наибольшее значения функции f(x, y, z) в области V, то справедливо неравенство mV £ Iv £ MV, где V – объем области, Iv – трехкратный интеграл от f(x, y, z) по области V. 3. (теорема о среднем) Трехкратный интеграл Iv от непрерывной функции f(x, y, z) по области V равен произведению ее объема V на значение функции в некоторой точке Р области V:
Приведенные свойства трехкратного интеграла позволяют доказать теорему о вычислении тройного интеграла:
Тройной интеграл от функции f(x, y, z) по правильной области V равен трехкратному интегралу по этой же области:
(Как и в случае двукратного интеграла, можно изменить порядок интегрирования, если это позволяет сделать форма области V. Можно с этой целью разбить область V на части). Если подинтегральная функция f(x, y, z) = 1, то тройной интеграл по области V дает значение ее объема Пример:
Нередко вычисление тройных интегралов значительно упрощается при переходе к цилиндрическим или сферическим пространственным координатам. В цилиндрических координатах положение точки Р определяется тремя числами r, j, z, где r и j – полярные координаты проекции точки Р на плоскость хОу, а z – аппликата точки Р. Пространственную область V разбивают на элементарные координатными поверхностями j = ji, r = rj, z = zk. Элементарный объем dV примет вид: dV = rdrdjdz, а тройной интеграл: х = rcosj, y = rsinj, z = z несложно перейти от декартовых координат к цилиндрическим: Пример: В сферических координатах положение точки Р определяется числами j, r, q, где r – расстояние точки от начала координат, q – угол между r и осью Оz и j – угол между проекцией r на плоскость хОу и осью Ох (отсчитывается, как обычно, от оси Ох против часовой стрелки). Декартовы координаты связаны со сферическими так: х = rsinqcosj, у = rsinqsinj, z = rcosq (0 £ r £ ¥, 0 £ j £ 2p, 0 £ q £ p). Элемент объема в сферических координатах dV = r2sinqdrdjdq. В итоге можем перейти от тройного интеграла в декартовых координатах к тройному интегралу в сферических координатах.
Пример:
Криволинейный интеграл. Криволинейный интеграл по длине дуги (I рода). Пусть функция f(x, y) определена и непрерывна в точках дуги L гладкой кривой, заданной уравнением у = j(х), где х Î[a, b]. Разобьем дугу L произвольным образом на n элементарных дуг точками А = А0, А1, …,Аn = В (А и В – точки начала и конца дуги L) и обозначим через Dsi длину i – ой элементарной дуги. На каждой элементарной дуге выберем произвольную точку Mi(xi, hi) и умножим значение функции f (xi, hi) в этой точке на длину Dsi соответсвующей дуги. Интегральной суммой для функции f(x, y) по длине дуги L называется сумма вида Криволинейным интегралом по длине дуги L от функции f(x, y) называется предел интегральной суммы (8.1) при условии, что maxDsi ® 0.
ds – дифференциал дуги; n ® ¥ (при maxDsi ® 0). Кривую L называют нередко контуром интегрирования.
Этот интеграл мало отличается от рассмотренного ранее определенного интеграла (разница в том, что Dsi > 0 всегда) и, соответственно, свойства его таковы: 1. Криволинейный интеграл I рода не зависит от направления пути интегрирования, т.е. 2. Интеграл суммы равен сумме интегралов
3. Постоянную можно выносить из под знака интеграла
4. Если контур интегрирования L разбит на две части L1 и L2, то
Пример: Вычислить
Отметим, что: 1. Приведенные утверждения справедливы и в случае, если дуга L – кусочно гладкая. (Напомним, что кривая называется гладкой, если касательная к ней определена и непрерывна в каждой точке, а кусочно гладкой – кривая, состоящая из конечного числа гладких кусков). 2. Возможен (а зачастую и целесообразен) переход к полярным координатам или к параметрическому заданию функции у = j(х), упрощающий вычисление криволинейного интеграла I рода. 3. Если f(x, y) > 0, то этот интеграл численно равен массе кривой L, имеющей переменную линейную плотность j = f(x,y). (Используется для вычисления массы криволинейных конструкций, их моментов инерции и т.д.). 4. Аналогично (8.2) определяется интеграл, если дуга L есть часть пространственной кривой, в каждой точке которой задана функция, т.е.
Криволинейный интеграл по координатам (II рода). Пусть функции f1(x, y) и f2(x, y) непрерывны в точках дуги АВ гладкой кривой, заданной уравнением у = j(х), где х Î[a, b]. Интегральной суммой для функций f1(x, y) и f2(x, y) по координатам называют сумму вида где Dхi и Dyi – проекции элементарной дуги Ds на оси Ох и Оу. Криволинейным интегралом по координатам от выражения f1(x, y)dx + f2(x, y)dy по направленной дуге АВ называется предел интегральной суммы (8.4) пр и условии, что maxDxi ® 0 и maxDуi ® 0:
Рассмотрим основные свойства криволинейного интеграла второго рода. 1. Криволинейный интеграл второго рода меняет знак на противоположный при изменении направления пути интегрирования:
2. Криволинейный интеграл второго рода равен сумме таких же интегралов по каждой из координат в отдельности:
Другие свойства аналогичны свойствам интеграла первого рода. Криволинейный интеграл второго рода может быть вычислен по формуле: Аналогичная формула используется, если требуется вычислить криволинейный интеграл второго рода по пространственной кривой
Пример:
Криволинейный интеграл II рода численно равен работе, совершаемой переменной силой `F = `if1(x, y) + `jf2(x, y) на соответствующем криволинейном пути АВ.
Формула Грина. Это важное во многих приложениях соотношение позволяет установить связь между двойным интегралом по некоторой плоской области D и криволинейным интегралом второго рода по границе L этой области. Если функции f1(x, y) и f2(x, y) вместе со своими частными производными называемое формулой Грина. (Символ замкнутому контуру). Двойной интеграл в (8.7) вычисляется, как обычно, сведением его к двукратному. Использование (8.7) позволяет во многих случаях существенно упростить решение задачи.
Тесты
1) по оси Ох; 2) по оси Оу; 3) правильной.
3.22. Область Д ограничена линиями 1) 3.23. Дан 1) 3.24. Объем тела, ограниченного поверхностями 1) 3.25. Область V ограничена поверхностями х = 0, х = 2, у = 0, у = 3, z = 0, z = 4, 1) 696; 2) 382; 3) –154; 4) 232.
3.26. Объем тела, ограниченного поверхностями 1) 3.27. Криволинейным интегралом I рода называют: 1) 2) 3) 3.28. На полукубической параболе 1) 3.29. Для криволинейного интеграла II рода 1) 3.30. Отрезок соединяет точки А(1; 1) и В(3; 4). 1)
|
||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.68.50 (0.088 с.) |
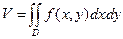 (7.9).
(7.9).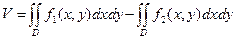 (7.10)
(7.10)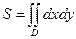 или, если область D правильная
или, если область D правильная 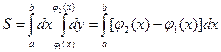 (7.11).
(7.11).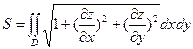 (7.12).
(7.12).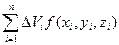 . Устремляя максимальный диаметр maxdi (и, соответственно, объем DVi) к нулю (maxdi ® 0) перейдем к пределу интегральной суммы. При условиях, перечисленных выше, этот предел существует и называется тройным интегралом:
. Устремляя максимальный диаметр maxdi (и, соответственно, объем DVi) к нулю (maxdi ® 0) перейдем к пределу интегральной суммы. При условиях, перечисленных выше, этот предел существует и называется тройным интегралом: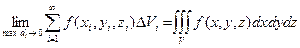 (7.13).
(7.13).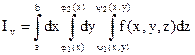 (7.14)
(7.14)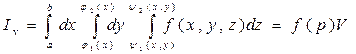
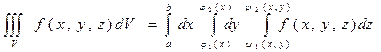 (7.15)
(7.15)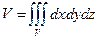 (7.15`).
(7.15`).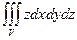 , если область V определяется неравенствами: 0 £ х £ ½, х £ у £ 2х, 0 £ z £
, если область V определяется неравенствами: 0 £ х £ ½, х £ у £ 2х, 0 £ z £ 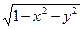 (т.е. а = 0, b = ½, j1(x) = x, j2(x) = 2x, y1(x,y) = 0, y2(x,y) =
(т.е. а = 0, b = ½, j1(x) = x, j2(x) = 2x, y1(x,y) = 0, y2(x,y) = 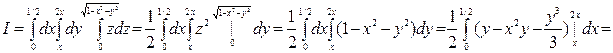
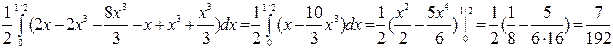
 , пределы интегрирования в соответствующем трехкратном интеграле определятся формой области V. Зная формулы связи:
, пределы интегрирования в соответствующем трехкратном интеграле определятся формой области V. Зная формулы связи: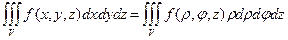 .
.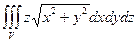 , если область V ограничена цилиндром х2 + у2 = 2х и плоскостями у = 0, z = 0, z = a. Перейдем к цилиндрическим координатам. Уравнение цилиндра примет вид r2cos2j + r2sin2j = 2rcosj => r2(cos2j + sin2j) = 2rcosj => r = 2 cosj. Область V определяется неравенствами: 0 £ r £ 2cosj, 0 £ j £ p/2, 0 £ z £ а и
, если область V ограничена цилиндром х2 + у2 = 2х и плоскостями у = 0, z = 0, z = a. Перейдем к цилиндрическим координатам. Уравнение цилиндра примет вид r2cos2j + r2sin2j = 2rcosj => r2(cos2j + sin2j) = 2rcosj => r = 2 cosj. Область V определяется неравенствами: 0 £ r £ 2cosj, 0 £ j £ p/2, 0 £ z £ а и 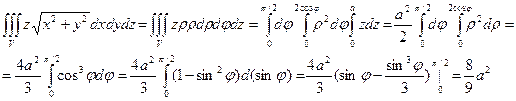
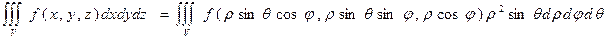
 , если область V – верхняя половина шара x2 + y2 + z2 £ r2. Перейдя к сферическим координатам получим: 0 £ r £ r, 0 £ j £ 2p, 0 £ q £ p/2, x2 + y2 = r2sin2qcos2j + r2sin2qsin2j = r2sin2q и
, если область V – верхняя половина шара x2 + y2 + z2 £ r2. Перейдя к сферическим координатам получим: 0 £ r £ r, 0 £ j £ 2p, 0 £ q £ p/2, x2 + y2 = r2sin2qcos2j + r2sin2qsin2j = r2sin2q и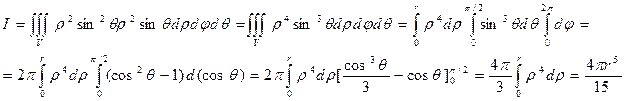
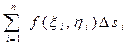 (8.1)
(8.1)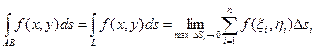 (8.2)
(8.2)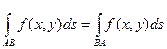 .
.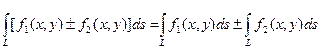
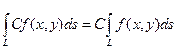 , где С = const.
, где С = const.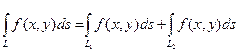 (полагаем, что эти части имеют одну общую точку). Можно показать, что криволинейный интеграл I рода сводится к определенному интегралу вида
(полагаем, что эти части имеют одну общую точку). Можно показать, что криволинейный интеграл I рода сводится к определенному интегралу вида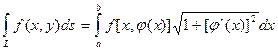 , где у = j(х) (8.3.).
, где у = j(х) (8.3.).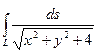 , где L – отрезок прямой, соединяющей точки О(0;0) и А (1;2). Уравнение прямой примет вид у = 2х и для этой функции
, где L – отрезок прямой, соединяющей точки О(0;0) и А (1;2). Уравнение прямой примет вид у = 2х и для этой функции 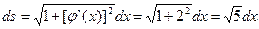 , откуда
, откуда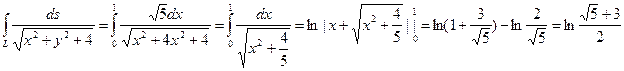
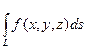 .
.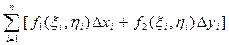 (8.4),
(8.4),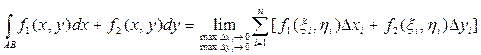 (8.5)
(8.5)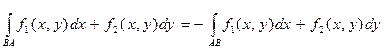 (это можно связать с тем, что в отличие от Dsi > 0, Dxi и Dyi могут быть и больше и меньше нуля).
(это можно связать с тем, что в отличие от Dsi > 0, Dxi и Dyi могут быть и больше и меньше нуля).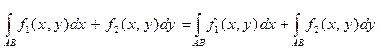 .
.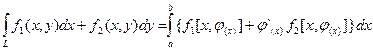 (8.6).
(8.6).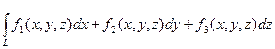 . В этом случае (и во многих случаях плоской кривой) целесообразно использовать параметрическое задание кривой.
. В этом случае (и во многих случаях плоской кривой) целесообразно использовать параметрическое задание кривой.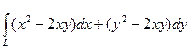 , где L – дуга параболы у = х2, от точки А(–1; 1) до точки В(1; 1). у = j(х) = х2 и j`(х) = 2х. По формуле (8.6)
, где L – дуга параболы у = х2, от точки А(–1; 1) до точки В(1; 1). у = j(х) = х2 и j`(х) = 2х. По формуле (8.6)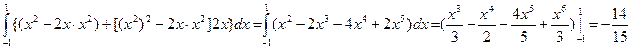 .
.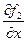 и
и 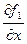 непрерывны в замкнутой области D (включающей границу L), то справедливо соотношение
непрерывны в замкнутой области D (включающей границу L), то справедливо соотношение 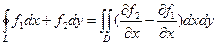 (8.7)
(8.7)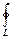 означает криволинейный интеграл по
означает криволинейный интеграл по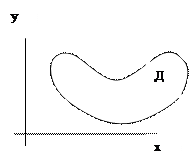 3.21. Область Д является правильной:
3.21. Область Д является правильной: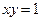 ;
;  ;
; 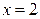 .
. 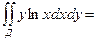
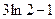 ; 2)
; 2)  ; 3)
; 3)  .
.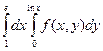 . Изменив порядок интегрирования получим:
. Изменив порядок интегрирования получим: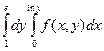 ; 2)
; 2)  ; 3)
; 3) 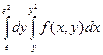 .
.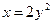 ,
, 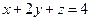 ,
,  ,
, 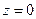 , составит (куб.ед)
, составит (куб.ед)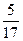 ; 2) 8; 3) –3; 4)
; 2) 8; 3) –3; 4) 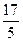 .
.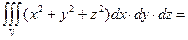
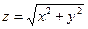 ,
, 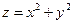 составит (куб.ед):
составит (куб.ед):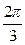 ; 2)
; 2)  ; 3)
; 3) 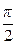 .
.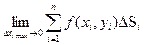 ;
;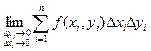 ;
; .
.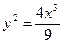 лежат точки А(3; 2
лежат точки А(3; 2 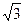 ) и В(8;
) и В(8; 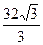 )
) 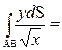
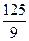 ; 2)
; 2)  ; 3) -
; 3) -  справедливо:
справедливо: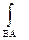 ; 2)
; 2) 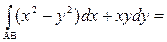
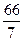 ; 2)
; 2) 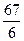 ; 3)
; 3)  ; 4)
; 4) 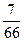 .
.